
Con il rientro sui banchi di scuola ci prepariamo ad accogliere i nostri studenti con attività di ripasso che attingono dalla vita quotidiana e da ciò che succede attorno a noi. Così, in vista delle elezioni politiche che si terranno il $25$ settembre, con i ragazzi che iniziano la classe terza affronteremo dal punto di vista numerico le regole di base della legge elettorale. In accordo con la collega di Lettere abbiamo deciso di riprendere il discorso riguardante l’educazione civica, cercando di aiutare gli studenti a comprendere meglio il contesto politico e normativo nel quale vivono. La nostra intenzione non è parlare di partiti e programmi elettorali, ma di discutere con i ragazzi di quella che è “l’arte e la scienza del governare”, il significato del termine politica, dal punto di vista etimologico e la sua origine greca.
La novità maggiore rispetto alle ultime elezioni, che gli studenti per mere questioni anagrafiche non possono ricordare, riguarda il numero dei parlamentari, ridotto a seguito di risultato referendario: i deputati passeranno da $630$ a $400$, i senatori da $315$ a $200$. Il primo quesito matematico che ci porremo sarà allora: a quali percentuali corrispondono queste diminuzioni? Riprenderemo così il concetto di variazione percentuale che esprime la differenza tra il valore finale e quello iniziale rapportato al valore iniziale ed espresso in percentuale. Farò notare ai ragazzi la presenza di calcoli con i numeri relativi, a cui presto si dovranno abituare, in quanto si parla di una diminuzione e dunque si ottengono risultati negativi.
Questo si traduce in:
| Valore finale | Valore iniziale | Rapporto | Percentuale | |
| Camera | $400$ | $630$ | $\dfrac{400-630}{630}\sim -0,365$ | $-36,5\%$ |
| Senato | $200$ | $315$ | $\dfrac{200-315}{315}\sim -0,365$ | $-36,5\%$ |
La riduzione è dunque stata analoga sia alla Camera che al Senato.
Il secondo punto da trattare riguarderà direttamente la legge elettorale e la suddivisione del metodo di elezione dei parlamentari. Infatti una parte del Parlamento è eletta tramite metodo proporzionale e l’altra mediante sistema maggioritario.
Daremo quindi lettura in classe di un articolo che fornisce alcune informazioni su cosa accadrà numericamente nel nostro Parlamento.
Alla Camera ci saranno $147$ collegi uninominali, in cui ogni partito o coalizione presenterà un solo candidato. In ogni collegio sarà eletto il candidato che prenderà almeno un voto in più degli altri. Per questo si chiama maggioritario, vince chi ha più voti.
Altri $245$ seggi saranno assegnati secondo un metodo proporzionale, sulla base di liste compilate dai partiti o dalle coalizioni. Quindi si ottiene un numero di posti proporzionale ai voti ricevuti.
Determineremo quindi le percentuali di come si suddividono gli eletti in base al metodo:
| Maggioritario | $\%$ Maggioritario | Proporzionale | $\%$ Proporzionale | |
| Camera | $147$ | $\dfrac{147}{400}=0,3675$ $0,3675\cdot 100\sim 37\% $ | $245$ | $\dfrac{245}{400}=0,6125$ $0,6125\cdot 100\sim 61\% $ |
Qualche alunno si dovrebbe a questo punto accorgere di non aver coperto il totale dei deputati e quindi si identificheranno i restanti $8$ seggi che saranno assegnati nelle circoscrizioni estere. Si potrà così approfondire l’importanza di parlamentari che rappresentano gli italiani residenti all’estero.
Passeremo poi all’analisi dei dati sul Senato per verificare la corrispondenza nelle percentuali. L’assegnazione dei $200$ seggi del Senato si baserà sullo stesso principio: $74$ seggi saranno assegnati in collegi uninominali, $122$ con metodo proporzionale e $4$ nelle circoscrizioni estere.
| Maggioritario | $\%$ Maggioritario | Proporzionale | $\%$ Proporzionale | |
| Senato | $74$ | $\dfrac{74}{200}=0,37$ $0,37\cdot 100= 37\% $ | $122$ | $\dfrac{122}{200}=0,61$ $0,61\cdot 100= 61\% $ |
In questo caso noteremo che le percentuali non sono da arrotondare, così possiamo determinare i numeri per la Camera dei Deputati per mantenere l’analoga distribuzione: essendo i deputati il doppio dei senatori si avranno $74\cdot 2=148$ con il sistema maggioritario e $122\cdot 2=244$ eletti con il proporzionale.
Riporteremo infine i dati su un foglio di calcolo e creeremo i grafici che rappresentano queste due situazioni.
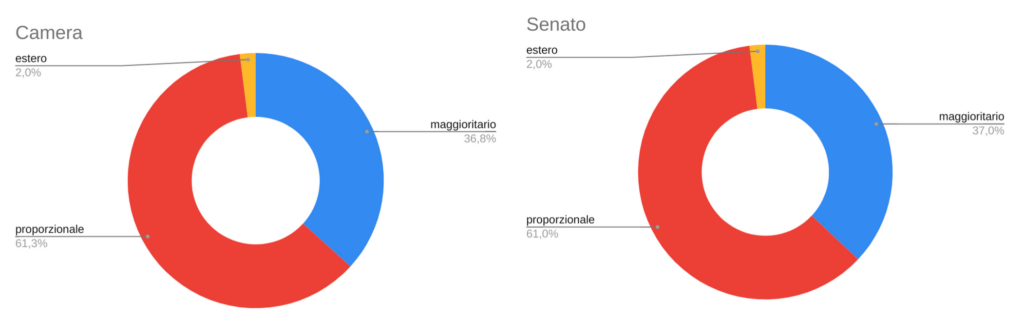
A conclusione dell’attività fin qui illustrata, gli studenti avranno il compito di cercare online o sui giornali cartacei alcune infografiche che descrivano la situazione studiata in aula.
