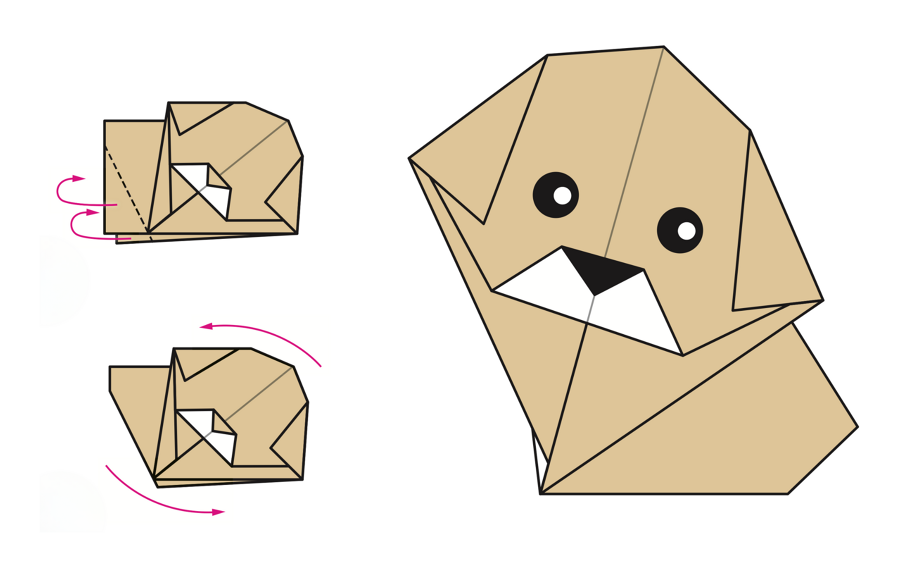
Prima di avviare la parte teorica sui poligoni, nella mia classe prima dedico un’ora di lezione introduttiva alla manipolazione con la carta. Ho notato, nel tempo, che studentesse e studenti hanno sempre meno manualità e testare regole grafiche con le pieghe degli origami spesso è per loro una sfida interessante. In quanto appassionata di cani, chiedo loro di realizzarne uno seguendo le istruzioni che proietto in classe:
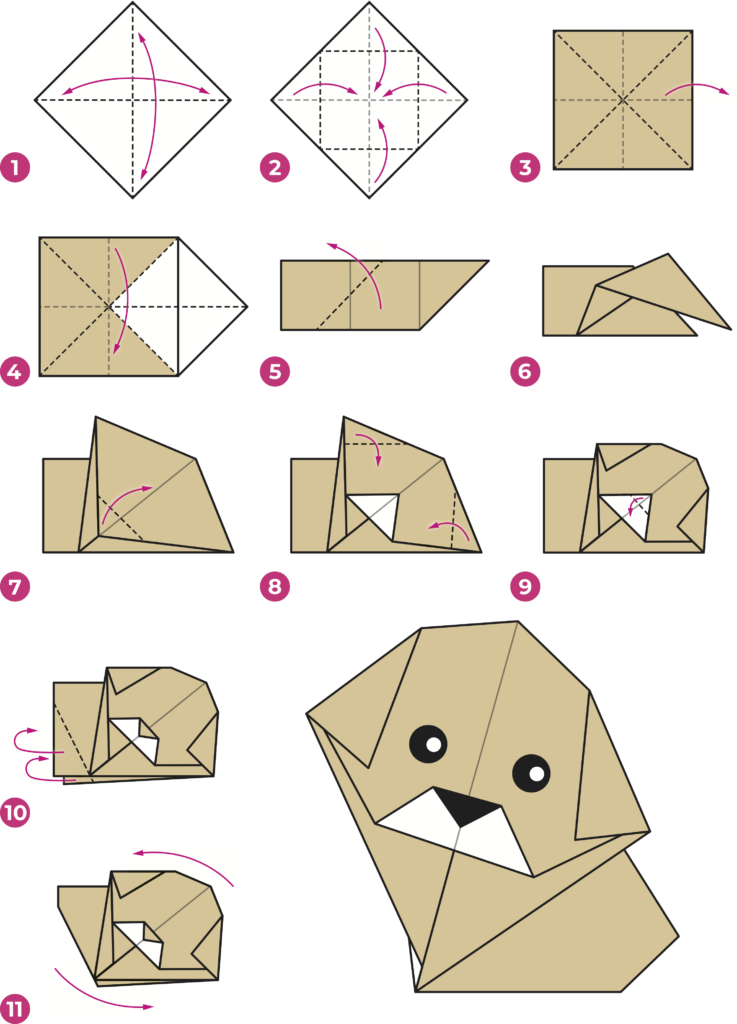
In rete si trovano molti siti sugli origami: ne seleziono qualcuno e, dopo il primo esercizio, lascio alle mie alunne e ai miei alunni la scelta di cosa creare.
Oltre ai passaggi manuali effettuati con la carta colorata da origami che porto in aula, le studentesse e gli studenti appuntano sul quaderno tutti i poligoni che individuano. Se non ne conoscono qualcuno, descrivono le figure che lo compongono e che sono in grado di riconoscere. In classe con questa attività laboratoriale spesso si creano tempi morti, perché alcuni studenti hanno una manualità più sviluppata di altri. Per questo lascio loro la possibilità di crearne a piacere in base all’abilità di ciascuno. Dopo circa $20$ minuti, ci fermiamo per fare un po’ di brainstorming e capire quali poligoni sono stati individuati. Scriviamo alla lavagna i nomi dei poligoni e cerchiamo di catalogarli, fissando alcune informazioni fondamentali per distinguerli. L’obiettivo è quello di arrivare alla definizione di poligono come “parte di piano delimitata da una spezzata chiusa semplice”.
A questo punto, possiamo passare all’attività che il nostro libro di testo Open Math ci propone (Unità $6$, pagina $224$ della versione tematica e unità G$6$, pagina $664$ della versione curricolare): sempre con carta, forbici e pieghe dimostriamo che la somma degli angoli interni di un triangolo è $180^{\circ }$. Questa attività in alcuni casi è già stata svolta alla scuola primaria ma mi permette di inserire i concetti di angoli interni ed esterni e di passare, nella lezione successiva, alla generalizzazione della formula
Somma angoli interni $=180^{\circ }\times \left( n-2\right)$
dove $n$ è il numero dei lati del poligono.