
Noi docenti di matematica sappiamo bene che il calcolo con le frazioni è probabilmente lo scoglio più difficile da superare durante la scuola media e, purtroppo, moltissimi dei nostri studenti si disinnamorano della matematica proprio con questo argomento. Oltretutto, la trattazione di questo importante nodo va a cadere proprio nel periodo dell’anno in cui le energie delle nostre classi sono al minimo.
Vi propongo allora un’attività leggera, ma significativa, per familiarizzare con le frazioni equivalenti unendo matematica, arte e manualità per ragionare in modo profondo sull’espansione e la semplificazione delle frazioni, ben oltre la regola “moltiplica sopra e sotto”.
L’idea è di lasciarsi ispirare dalle coperte patchwork, proprio quelle cucite a mano, fatte di pezzetti di stoffa diversi, uniti con pazienza e gusto; meglio ancora se ne abbiamo qualcuna da portare in classe con una bella storia personale da raccontare. Lo storytelling aiuterà a catturare l’attenzione e le emozioni positive che richiameremo saranno una colla fortissima per tenere appicciati anche i concetti matematici che vogliamo introdurre.
Nel patchwork un tassello si ripete, si moltiplica, si alterna con altri: il rapporto tra i colori si mantiene, ma la coperta cresce creando fantasie sempre più complesse e affascinanti; una metafora perfetta per espandere e semplificare le frazioni in modo concreto.
Si parte da un tassello base:
Per esempio, $2$ quadratini su $5$ sono a tinta unita, gli altri $3$ sono in fantasia (righe, pois, cuori, …); abbiamo così rappresentato la frazione $\dfrac{2}{5}$.

Se questo tassello viene affiancato $2$, $3$, $10$ volte per realizzare la coperta, la proporzione tra tinta unita e la fantasia resta invariata; allo stesso modo nelle frazioni i numeri diventano più grandi creando tante versioni equivalenti.

Questo lavoro si presta anche a semplici ragionamenti geometrici; infatti, con uno stesso tassello si possono creare tante versioni differenti della coperta in base a come si decide di ruotarli assemblandola.
Per esempio, con il tassello che rappresenta $\dfrac{1}{2}$ si possono ottenere queste e altre combinazioni.

Viceversa, se da una coperta grande si cerca di risalire al modulo originario, si può pensare di piegarla in $2$, $3$, $5$ parti uguali; così, dividendo in più passaggi una frazione si ricava quella ridotta ai minimi termini, lavorando sulla semplificazione.
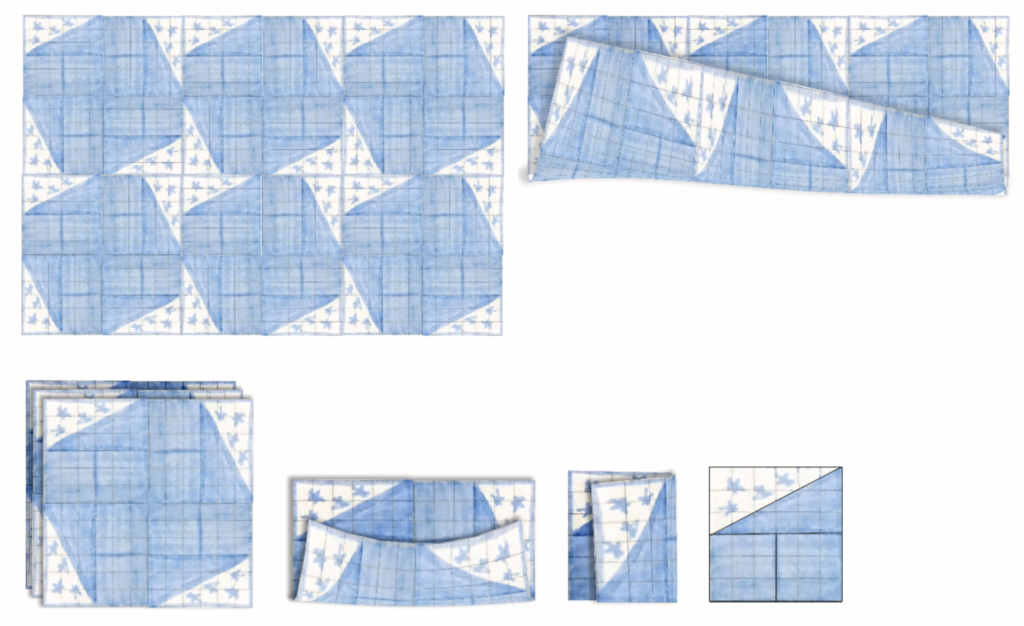
In entrambi i casi, alunne e alunni non solo vedono, ma toccano con mano il concetto di frazione equivalente.
La proposta si arricchisce con una parte laboratoriale e collaborativa: si divide la classe in gruppi e a ciascuno di questi viene assegnata una frazione di riferimento. In ogni gruppo si dovrà decidere come rappresentare la propria frazione usando una coloritura a tinta unita per il numeratore e una fantasia per gli altri frammenti del modulo base.
Questo passaggio può essere reso ulteriormente significativo chiedendo di tenere traccia delle varie proposte di rappresentazione e di sceglierne una più creativa; per esempio, nel mio tassello della frazione $\dfrac{3}{4}$ ho creato dei quarti di forma diversa, ma comunque equivalenti tra loro. Per farlo ho diviso il quadrato a metà e poi ho diviso ciascuna metà ancora a metà in modi diversi.
Successivamente, ogni gruppo creerà tanti tasselli e li unirà su un cartellone formando una coperta. Anche qui, si possono fare delle disposizioni temporanee e fotografarle per tenere traccia di quante combinazioni diverse si riescono a realizzare.
Una volta create le coperte definitive i gruppi potranno scambiarle per risalire alla frazione originaria, il tutto trascrivendo sempre sul quaderno i propri ragionamenti e calcoli.
Per finire, è bene organizzare un momento di confronto tra i diversi gruppi per raccogliere tutte le strategie emerse e formalizzare quanto fatto; poi, tutte le creazioni patchwork verranno appese in classe rendendo l’ambiente ancora più accogliente e personalizzato.
Una frazione è un rapporto, un ritmo, un disegno, una tessitura… e da oggi anche un modo per costruire insieme qualcosa di bello.
