
Il gioco che vi propongo nasce con l’obiettivo di combattere la dipendenza cronica degli studenti dalla calcolatrice, stimolandoli invece a fare stime e approssimazioni basate su semplici ragionamenti.
Come prima cosa dovete procurarvi un tabellone simile a quello del gioco dell’oca, con circa trenta caselle. Il passo successivo è costruire un mazzo di carte contenenti delle espressioni nelle quali i giocatori, di volta in volta, dovranno sostituire il valore ottenuto con il lancio del dado. Infatti, il numero di caselle del quale il giocatore dovrà avanzare (o retrocedere, se il numero ottenuto fosse negativo) sarà dato dalla parte intera del numero ottenuto sostituendo il valore del dado nell’espressione contenuta nella carta.
Il tipo di espressioni da inserire nelle varie carte dipende dalla classe in cui volete proporre il gioco e dagli argomenti che vi interessa ripassare.
Facciamo qualche esempio: se volete ripassare le frazioni, tra le carte del vostro mazzo potreste inserire le carte:
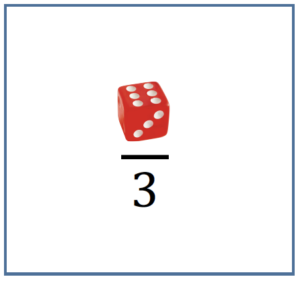
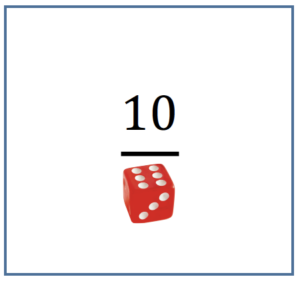
In questo caso, indicando con $n$ il punteggio ottenuto tirando il dado, se $n = 1$, $2$, la squadra che ha pescato la prima carta non sposterà il proprio segnalino, perché la parte intera di $\frac{1}{3}$ e di $\frac{2}{3}$ è $0$ (la parte intera di un numero è definita come il più grande numero intero minore o uguale al numero stesso), se $n = 3$, $4$, $5$ la squadra muoverà in avanti il proprio segnalino di una casella, mentre se $n = 6$ la squadra avanzerà di due caselle. Analogamente, la squadra che ha pescato la seconda carta sposterà in avanti il proprio segnalino di dieci caselle se $n = 1$, di cinque caselle se $n = 2$, di tre caselle se $n = 3$, di due caselle se $n = 4$, $5$ e di una sola casella se $n = 6$.
Per ripassare i radicali vi servirà un mazzo di carte contenenti espressioni con le radici. Per esempio, se avete messo nel mazzo le carte:
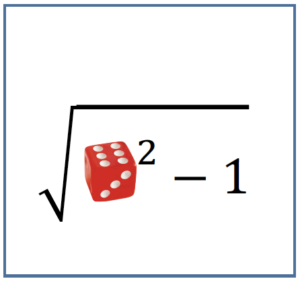
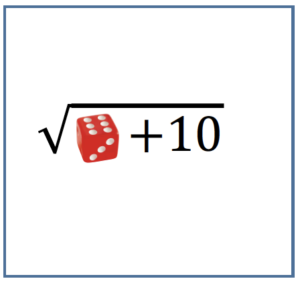
la squadra che pesca la prima carta e tirando il dado ottiene $6$ potrà muovere il proprio segnalino in avanti di cinque caselle (essendo la parte intera di $\sqrt {35}$ uguale a $5$), mentre la squadra che, avendo pescato la seconda carta, con il lancio del dado ottiene $6$ potrà muovere il proprio segnalino in avanti di quattro caselle (essendo la parte intera di $\sqrt {16}$ uguale a $4$).
Se invece volete utilizzare il gioco per ripassare i logaritmi, potreste inserire nel vostro mazzo carte del tipo:

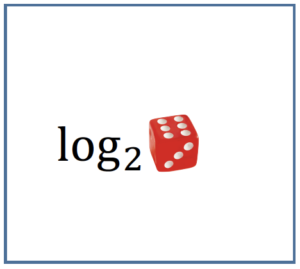
In questo caso, la squadra che pesca la prima carta dovrà muovere il proprio segnalino di un numero di caselle pari al doppio del punteggio ottenuto tirando il dado, mentre la squadra che pesca la seconda carta resterà ferma se $n=1$, si muoverà in avanti di una casella se $n=2$, $3$ e si muoverà in avanti di due caselle se $n=4$, $5$, $6$.
Infine, per un ripasso divertente sulle funzioni goniometriche, potreste utilizzare un mazzo contenente carte del tipo:
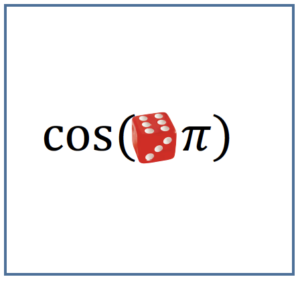
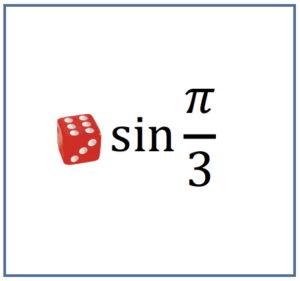
La squadra che pesca la prima carta dovrà muovere il proprio segnalino in avanti di una casella se $n$ è pari, mentre dovrà muoverlo indietro di una casella se $n$ è dispari. Analogamente, la squadra che pesca la seconda carta lascerà fermo il proprio segnalino se $n=1$, lo muoverà in avanti di una casella se $n=2$, $3$, di due caselle se $n=4$, $5$ e di tre caselle se $n = 6$.
Per giocare formate squadre di due o tre studenti. Durante il proprio turno di gioco, ogni squadra deve tirare un dado e pescare una carta. A questo punto la squadra calcola il numero di caselle di cui avanzare (o retrocedere) nel modo spiegato prima. Se la stima ottenuta è corretta, la squadra di turno muove il proprio segnalino di un numero di caselle pari al numero ottenuto, mentre se la stima ottenuta è errata la squadra retrocede di tre caselle. Dopo aver fatto la propria mossa la squadra ripone la carta pescata in fondo al mazzo. A questo punto il turno passa alla squadra successiva che procede nello stesso modo. Vince la squadra che raggiunge o supera il traguardo per prima.
