
Qualche anno fa mi capitava spesso di usare i mattoncini per le costruzioni nelle lezioni di Matematica perché erano il gioco più utilizzato dai miei figli. Ma si sa cosa succede ai figli, no? Arriva l’adolescenza e i mattoncini smettono di essere in giro per casa e tra i banchi.
Cercavo da tempo un’idea per riproporre una lezione particolarmente ben riuscita sulle proporzioni in cui avevo usato i mattoncini e, finalmente, ho trovato un modo per rimpiazzarli. Vi dirò di più, l’alternativa ha alcuni vantaggi: il materiale è personalizzabile in base alle esigenze e riproducibile in tante copie; quindi, tutte e tutti possono lavorare attivamente.
L’idea è quella di stampare delle griglie quadrettate (o triangolari o esagonali, largo alla fantasia) su carta colorata e poi ritagliarla nelle varie dimensioni necessarie.

Inizialmente proponiamo alla classe diverse composizioni ottenute sovrapponendo rettangoli di due colori differenti in varie forme (come in foto) e chiediamo a studentesse e studenti se le ritengono tra loro “proporzionate”.

Sorgeranno diversi pareri e ci auguriamo che nasca anche una discussione sul significato del termine “proporzionato”. Possiamo aspettarci che la maggior parte della classe sostenga che le composizioni non sono molto proporzionate e che qualcuno provi a motivare la sua posizione dicendo che alcune hanno molto verde rispetto al giallo, altre ne hanno pochissimo. Il concetto chiave è proprio questo “rispetto a”, li aiuteremo a ricordare che sanno già scrivere matematicamente questo tipo di relazione usando le frazioni e chiederemo di scrivere quelle che rappresentano le figure assegnate.

Ora possiamo partire da una composizione semplice scelta come riferimento (per esempio $1:4$) e chiedere di aggiustare le altre in modo che siano proporzionate. Cominciamo a proporre esempi molto semplici con rettangoli gialli che siano il doppio o il triplo di quello di partenza, così che sia abbastanza evidente come piazzare i pezzi verdi.

Poi complicheremo un po’ la faccenda proponendo rettangoli che hanno lo stesso numero di quadratini dei precedenti, ma con una forma diversa.

Facciamo sempre scrivere la frazione corrispondente e facciamo notare che tutte possono essere ridotte ai minimi termini nella frazione di partenza.

Infine, proviamo a fornire dei rettangoli che non siano multipli di quello di partenza per mostrare che non sempre è possibile trovare una composizione proporzionata a quella di partenza.
Possiamo proseguire ad utilizzare questo materiale per far scrivere delle proporzioni e per far verificare la proprietà fondamentale.
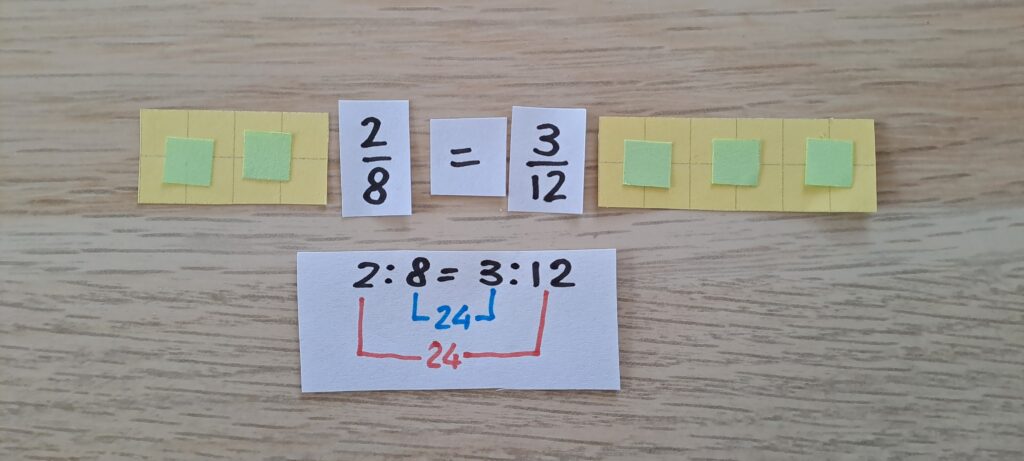
Ci tornerà utile anche per proporre alcuni semplici problemi; per esempio, possiamo proporre una composizione di partenza e un rettangolo giallo, chiedendo di calcolare quale rettangolo verde vada abbinato e viceversa.

In questo modo avremo introdotto le proporzioni e lavorato sulle strategie di risoluzione dei problemi in modo efficace e indolore, facendo leva su conoscenze e abilità già acquisite e rendendo tangibili dei concetti astratti.
