
Vi propongo un compito colorato per le vacanze: coinvolgeremo le ragazze e i ragazzi nella creazione di piccoli murales ottenuti con tessere origami bicolori, con l’obiettivo matematico di riflettere su aree, perimetri e frazioni.
Le studentesse e gli studenti dovranno piegare nove modelli tradizionali di menko seguendo il diagramma di piegatura e progetteranno dei murales geometrici, studiandone alcune proprietà. Una volta tornati in aula, ogni studente potrà appenderne uno alla parete, per creare un murale di classe.
Le ragazze e i ragazzi partiranno da carta quadrata bianca di lato $15$ cm (anche ritagliata dai fogli a quadretti di vecchi quaderni). Nella descrizione, per maggior chiarezza i due fogli sono colorati diversamente.
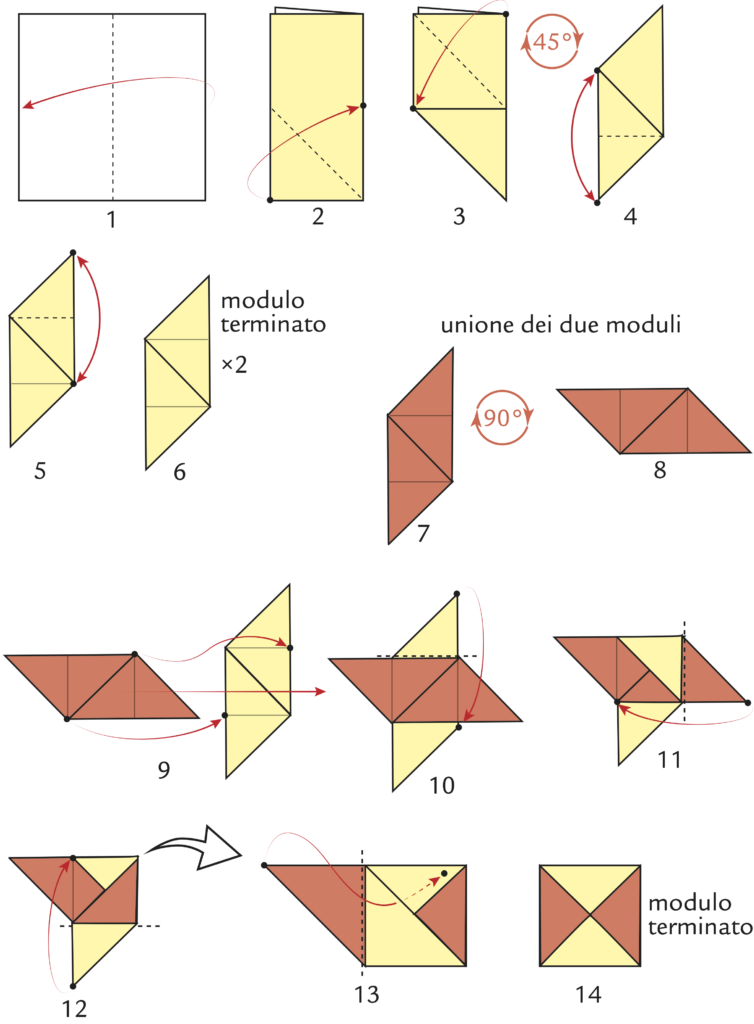
Istruzioni di piegatura
1. Porta un lato sul lato opposto.
2. Tenendo il rettangolo ottenuto poggiato sul lato corto (come mostrato in figura), porta il lato corto più basso su quello lungo alla sua destra.
3. Porta il lato corto in alto sul lato lungo a sinistra; si ottiene un parallelogramma, diviso in due triangoli rettangoli, come mostra la figura nel passaggio 4.
4. È possibile ruotare il modello di $45$° per avere i lati lunghi del parallelogramma in posizione verticale, come mostra la figura. Considerato il lato lungo del parallelogramma a sinistra, porta un suo vertice sull’altro e riapri.
5. Ripeti sul lato lungo a destra.
6. Ripeti la costruzione con un altro foglio di carta (che è disegnato in arancione nel passaggio 7). Attenzione a eseguire nella stessa direzione il passaggio 2.
7-8. Ruota il secondo modulo di $90$°, arrivando a posizionarlo come mostra la figura 8.
9. Fai scivolare il modulo arancione su quello giallo.
10. Considera l’aletta gialla appartenente al modulo che sta sotto e che si trova in alto e piegala sul quadrato centrale.
11. Prosegui in senso orario, piegando al centro l’aletta arancione che si trova a destra.
12. Prosegui in senso orario, piegando al centro l’aletta gialla che si trova sotto.
13. Piega ora l’ultima aletta arancione, intascandola sotto la prima aletta gialla piegata.
14. Ecco il menko completato.
Osserviamo che sulla parte superiore il quadrato è diviso in quattro triangoli, mentre la faccia inferiore è un quadrato uniforme giallo, in riferimento al diagramma, bianco (a quadretti) per le studentesse e gli studenti.
Fate poi costruire altri otto menko, tutti bianchi. Successivamente studentesse e studenti scelgono il proprio colore preferito, sulla faccia superiore di tre menko colorano un solo triangolo, su altri tre menko colorano due triangoli adiacenti e sugli ultimi tre due triangoli opposti.
Nella foto vi mostro i miei menko bianchi e neri.

Utilizzando sia le facce superiori bicolori sia le facce inferiori bianche, potete proporre delle attività di composizione di configurazioni quadrate dove la parte colorata e quella bianca soddisfino alcune proprietà.
Ecco alcuni esempi di configurazioni e alcune domande che potete fare:

- Se fissiamo come unitaria l’area di un menko, che area hanno le figure nere formate all’interno del quadrato formato dai $9$ menko? E i loro perimetri?
Per esempio, nella prima configurazione, l’area della parte nera vale $1$, mentre nella seconda configurazione vale $2$.
Osserviamo che, in generale, per i perimetri occorre conoscere la misura della diagonale del quadrato, mentre l’area è sempre calcolabile con un numero intero se prendiamo come unità di misura uno dei triangolini.
- Se fissiamo come unità di misura uno dei quattro triangolini nei quali resta diviso ogni menko, quanto vale la parte colorata del quadrato composto dai $9$ menko, rispetto al quadrato stesso?
In questo caso lavoriamo con le frazioni: nella prima figura la parte nera vale $\dfrac{4}{36}$, mentre nel secondo caso vale $\dfrac{8}{36}$.
Buon lavoro e buone vacanze!
In Zona Matematica, nell’area dedicata agli origami, trovate l’attività completa che potete mettere a disposizione delle vostre studentesse e dei vostri studenti per delle vacanze colorate e dinamiche.
Vai all’area “Origami” del I grado
Vai all’area “Origami” del II grado – I biennio
