
Quest’anno, dopo tre anni di assenza, dedicati al lavoro editoriale, anch’io rientro a scuola.
Lo faccio dopo aver partecipato a una interessante scuola di didattica della Matematica, che mi ha fornito parecchi spunti di lavoro, e dopo aver avuto scambi altrettanto interessanti con altri docenti, inclusi quelli che saranno i miei nuovi colleghi: si va dai massimi ai minimi sistemi, ma vorrei concentrarmi per ora sui minimi.
Avendo avuto notizia che insegnerò in classi del primo biennio del liceo scientifico, mi sono chiesto che cosa potrei proporre come attività di inizio anno – per così dire, di “accoglienza matematica”.
Il primo dei vari “minimi” che sono scaturiti dalle discussioni è (vedi figura): “La divisione, fatta così, non si può vedere!”
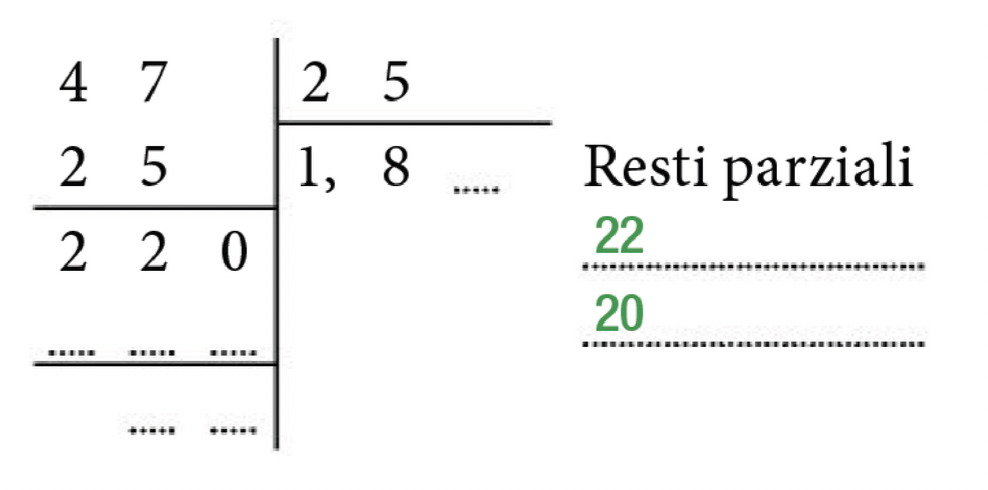
“Perché? Che cosa c’è che non va?”
“Ma perché non si fa la sottrazione per iscritto: la si fa a mente!”
Ora, a parte il fatto che reputo importantissimo il calcolo mentale, ma non mi sembra particolarmente significativo applicarlo in un contesto come questo, se questo fosse l’inizio di un’attività di laboratorio in cui esploro i resti parziali di una divisione e stessi dando le istruzioni a un software per eseguire la divisione passo passo, la sottrazione non si farebbe a mente, perché il software a mente, le sottrazioni, non le sa fare.
Dunque? Dunque per quanto riguarda le massime conclusioni rimando al finale di questo articolo, ma per quanto riguarda i “minimi” penso che una bella attività di accoglienza per le classi prime potrebbe essere dedicata a far capire come mai dividendo due numeri naturali, mal che vada, si ottiene un quoziente decimale illimitato periodico.
Qui potete trovare un esempio di attività di questo genere.
L’attività andrebbe pure curvata su ciò che accade quando il divisore è $0$. Le ragazze e i ragazzi non hanno sempre chiaro, per esperienza, il motivo per cui non si possa dividere per $0$: talvolta resta loro poco chiaro fino all’università. Facciamoglielo toccare con mano.
Sempre per restare in tema di divisione, il secondo “minimo” scaturito dalle discussioni è: “Ma tu Ruffini lo fai?”.
So che la regola di Ruffini è una questione divisiva. Serve o non serve? Una parte dei docenti italiani risponderebbe, in tutta tranquillità, “non serve”. Un’altra parte, probabilmente, è già scandalizzata solo per il fatto che la domanda sia stata posta.
Io, da parte mia, innanzitutto eliminerei la parola “regola”: sarà poco, ma aiuta a sfatare quel mito per cui la matematica “sono solo regole”. Dico “aiuta” perché per eliminare del tutto questa idea ci vuol ben altro. Comunque la parola regola ha un’accezione negativa e può benissimo essere rimpiazzata da “metodo”, “procedura”…
Sarebbe in ogni caso auspicabile mostrare che il metodo di Ruffini non è altro che una versione semplificata del metodo generale, far capire che quelle tre linee orizzontali e verticali che bisogna tracciare sono solo una convenzione. Insomma, far comprendere che è solo uno schema e, magari, aiuterebbe buttarlo dentro a un foglio elettronico, per concludere che, una volta acquisito, resta calcolo, cioè una piccola parte di ciò di cui si occupa la matematica.
Terzo minimo. “Ma a voi delle superiori serve che noi alle medie facciamo i prodotti notevoli?”
“Sinceramente no”, posso dirlo?
Allora qui mi vengono in mente le classi seconde del liceo. Rientrano dalla prima dopo aver più o meno digerito una montagna di calcolo letterale, “pronte” per digerirne un altro blocco, ben più indigesto: quello sui radicali, senza i quali, qualcuno un giorno mi ha detto, “non si può vivere”.
Come accogliere le ragazze e i ragazzi di seconda?
Beh, ho pensato, proviamo a dare un senso a questo calcolo letterale. Facciamo vedere, se già non l’abbiamo fatto, che l’algebra serve per dimostrare (“ma allora non ci sono solo le dimostrazioni di geometria!” “No”) e per risolvere problemi.
Vi propongo due attività (qui la prima, “Algebra per dimostrare”, e qui la seconda, “Interrogare una formula”) che si possono fare, prima di partire con il minestrone freddo dei radicali: si tratta di questioni semplici, ma forse aiutano a far capire che la matematica non è solo “risolvere” espressioni, ma che queste espressioni possono avere un senso nel risolvere per davvero alcuni problemi.
In queste due attività si trovano il calcolo letterale, la scomposizione di polinomi, finalizzati, in un caso, alla soluzione di un problema e, nell’altro, a enunciare un teorema.
Per questo ho usato prima il termine “risolvere”, scrivendolo una volta tra virgolette e un’altra volta senza. Le espressioni, numeriche o letterali, non si risolvono: casomai si trasformano, si semplificano, si riducono a un numero o a un’espressione equivalente, applicando tecniche di calcolo. Sono i problemi, invece, quelli che si risolvono per davvero, ivi inclusi i problemi di tipo dimostrativo.
Veniamo quindi ai “massimi” sistemi e all’augurio che voglio rivolgere per quest’anno scolastico alle colleghe e ai colleghi, compreso me.
Che sia un anno scolastico di “accoglienza matematica”, fuori o, almeno, un po’ più fuori del solito, dagli schemi, dalle regole e dentro o, almeno, un po’ più dentro del solito, ai problemi della matematica.
Le attività proposte in questo articolo sono tratte da “Matematica allo specchio edizione Blu – Primo biennio” edito da Ghisetti & Corvi.
