
Nella tradizione scolastica siamo soliti introdurre la probabilità parlando di dadi, mazzi di carte, urne. A volte viene da chiedersi se la probabilità non sia al mondo solo per i lanci di dadi, i giochi con le carte, le urne…
Che poi, queste “urne” richiamano anche immagini macabre e ci tocca spiegare che vanno bene anche un sacchetto o una scatola.
Non intendo oggi ribaltare la tradizione, però vorrei far vedere alcuni strumenti e alcune attività che ci permettono di simulare questi eventi probabilistici, andando addirittura in tre dimensioni.
Un percorso, questo, che possiamo portare avanti per tutto un quinquennio.
È facile, con un software, simulare il lancio di un dado. Ed è utile perché, se si vogliono simulare, per esempio, $100$ lanci di un dado e poi magari ripetere la stessa simulazione per $10$, $20$, $30$ volte, di certo non conviene entrare in classe con $10$, $20$, $30$ dadi e chiedere a ciascuno studente o studentessa di lanciare il dado $100$ volte e di annotare quante volte è uscito un certo numero, per esplorare la validità o meno della definizione frequentista di probabilità.
Nessuno impedisce di farlo, ma possiamo ottenere un risultato simile in pochi minuti con un software. A questo proposito, vi propongo un’attività il cui scopo è quello di mettere in evidenza il legame fra la definizione classica e la definizione frequentista di probabilità.
Tutto potrebbe iniziare da una domanda come la seguente.
Che cosa si verifica se si ripete una prova casuale per un grande numero di volte?
Considera il lancio di un dado regolare a sei facce e l’evento «esce il numero $5$»: la sua probabilità, secondo la definizione classica, è $\dfrac{1}{6}$.
Supponi ora di lanciare molte volte il dado e di annotare quante volte esce la faccia che riporta il numero $5$, cioè la frequenza con cui l’evento si verifica.
Al crescere del numero totale di lanci, il rapporto fra il numero di uscite favorevoli e il numero totale di lanci permette di fare una stima della probabilità di uscita del $5$.
Sulla base di queste considerazioni si può definire una misura di probabilità basata su prove ripetute, purché esse avvengano tutte nelle stesse condizioni.
Tra l’altro si pone anche un ulteriore interrogativo interessante: chi ci assicura che, lanciando un dado fisicamente, siamo proprio sempre nelle stesse condizioni? Forse un software realizza meglio la casualità dell’evento, ma l’interrogativo resta aperto.
E se i dadi sono due? La questione si complica un po’, ma niente paura. In quest’altra attività andiamo ancora a verificare la definizione frequentista, facendo ricorso alla somma dei punteggi che si ottengono lanciando due dadi.
Una simulazione come quella appena vista potrebbe anche essere utile con la somma dei punteggi di tre dadi per introdurre il calcolo combinatorio: se il Granduca di Toscana avesse avuto un foglio di calcolo…
E se i dadi venissero lanciati uno alla volta? Beh, ci si può sbizzarrire, per esempio inventando eventi dipendenti. Nell’attività che segue simuliamo il lancio di due dadi, uno a sei e uno a quattro facce, esplorando la probabilità condizionata.
Ma con tre dadi e il software si possono fare meraviglie.
Guardate qui come si può usare la probabilità per introdurre le coordinate cartesiane nello spazio.
Tutto nasce da un quesito Kangourou del $2018$.
Alberta lancia tre dadi equi a sei facce (numerate da $1$ a $6$) e scrive su un foglio il più alto dei numeri che ottiene. Lancia i tre dadi altre due volte, sempre scrivendo il più alto dei numeri ottenuti, e poi somma i tre numeri che ha scritto. Qual è la probabilità che la somma sia $18$?
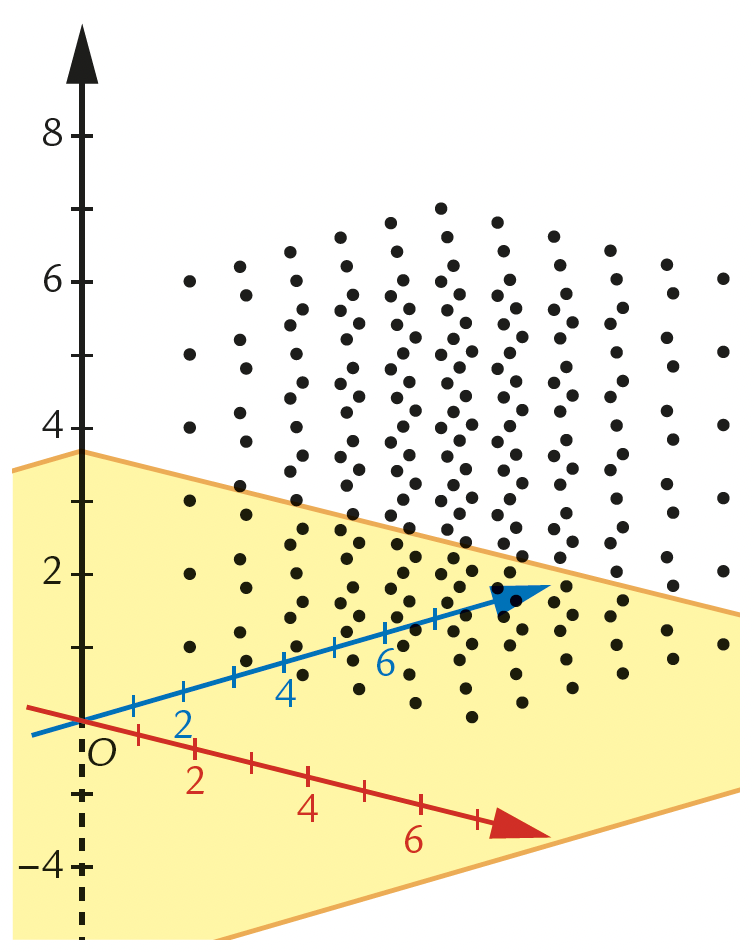
In sintesi, l’attività permette di esplorare in tre dimensioni il lancio di tre dadi a sei facce, costruendo uno spazio campione di forma cubica.
Successivamente si evidenziano con un colore diverso i casi favorevoli, in modo che sia più semplice contarli.
Bene. Terminato il nostro viaggio con la probabilità nello spazio in due e tre dimensioni, non resta che la quarta: il tempo.
Non viaggeremo nel tempo infinito, ma in un tempo finito: quello di un anno solare.
Conoscete il Paradosso del compleanno? Esso fu formalizzato nel $1939$ da Richard von Mises, matematico di origine ucraina, nato in un’epoca in cui l’Ucraina faceva parte dell’Impero Austro – Ungarico, poi naturalizzato statunitense.
La domanda seguente sembra avere una risposta scontata.
Pensi che sia più probabile ottenere «testa» lanciando una moneta equilibrata o che nella tua classe ci siano almeno due persone che hanno la stessa data di compleanno? Prova a rispondere senza rifletterci troppo, affidandoti all’intuito.
Chiunque sia a digiuno di probabilità è sicuramente portato a pensare che sia molto più grande la probabilità di ottenere «testa» rispetto alla probabilità che, in un gruppo di persone, ce ne siano almeno due nate nello stesso giorno dell’anno.
Per questo il problema viene chiamato paradosso anche se paradosso non è. Diciamo piuttosto che la sua risoluzione conduce a un finale del tutto controintuitivo: in un gruppo di persone sufficientemente numeroso, quale quello di una classe di scuola, calcolando la probabilità si arriva a una conclusione stupefacente.
Potete trovare l’attività qui.
Con il calcolo combinatorio si determina la probabilità di trovare due persone nate nello stesso giorno in un gruppo di $25$ persone, dopodiché si costruisce la funzione $p\left( x\right)$ che rappresenta la probabilità di trovare due persone nate nello stesso giorno in un gruppo di $x$ persone. È anche un’occasione per mostrare un’altra volta come l’idea di funzione permei trasversalmente tutti gli argomenti che si affrontano nel quinquennio. E, per di più, in questo caso, si costruisce una funzione del tutto inusuale: $p\left( x\right)=1-\dfrac{365!}{365^{x}\left( 365-x\right) !}$.
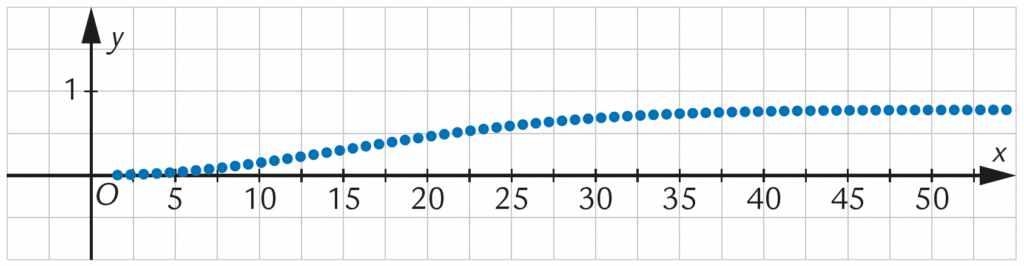
Come non concludere ancora una volta che la matematica è sorprendente?
L’augurio è di sorprendere sempre chi ci ascolta.
Buona probabilità!
Le attività proposte in questo articolo sono tratte da “Nuova Matematica allo specchio edizione Verde” e da “Matematica allo specchio”, i corsi di Matematica editi da Ghisetti & Corvi.



