
Sappiamo che i Pitagorici erano soliti rappresentare i numeri naturali con dei sassolini, che disponevano a formare figure geometriche, quali triangoli, quadrati eccetera.

Queste configurazioni possono dare luogo a figure piane, ma anche a figure tridimensionali, quali piramidi, cubi e così via.
Possiamo quindi parlare di numeri figurati.
Si viene così a creare un interessante collegamento tra i numeri e la geometria, più calato nella realtà di quanto possa sembrare, visto che è molto più usuale trovare attorno a noi configurazioni geometriche che hanno a che fare con i numeri piuttosto che, per esempio, risolvere un’espressione come questa:
$\begin{aligned}\frac{\left\{\left[\left(10+10^2\right):10\right]\cdot121\right\}^4:\left(11^5\right)^2-10^2}{\left(7^9\cdot7^4\right):\left(7^6\right)^2}\end{aligned}+100^{2}:\left( 10^{0}+99\right) ^{2}$
Ma c’è di più. Lo studio di queste configurazioni può essere utile per dare un significato all’algebra, quando viene usata per dimostrare, per ricavare relazioni, e non solo per svolgere calcoli, come per esempio questo:
$\left( \dfrac{1}{x^{3}-1000}+\dfrac{1}{x^{2}+10x+100}\right):\dfrac{x^{3}+x^{2}-90x}{x^{3}+10x^{2}+100x}\begin{aligned}:\frac{1}{x^2-20x+100}\end{aligned}$
Non voglio sminuire l’importanza di far acquisire alle nostre allieve e ai nostri allievi gli strumenti del calcolo, ma è di certo fondamentale spezzarne la monotonia proponendo loro concetti e collegamenti, per far comprendere il significato e l’utilità vera del calcolo stesso.
Molto spesso questi collegamenti vengono proprio dal mondo dei numeri. Quelli figurati, in particolare, offrono uno spunto interessante per mostrare come l’algebra sia uno strumento di generalizzazione e anche per acquisire il ragionamento per induzione, caratteristico dei numeri naturali.
Prendiamo per esempio i numeri triangolari.
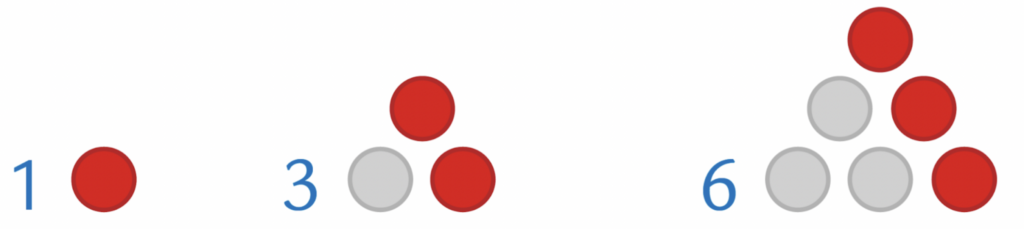
C’è una regolarità? Quale sarà il successivo?
Beh, si parte da $1$, poi si aggiunge $2$ per ottenere $3$, poi $3$ per ottenere $6$. Quindi al passo successivo aggiungeremo $4$, per ottenere $10$. Il gioco è presto capito: ogni volta aggiungiamo il naturale successivo.
$3=1+2$
$6=1+2+3$
$10=1+2+3+4$
C’è sotto il concetto di successione, nella sua rappresentazione con il suo termine generale; l’ennesimo numero triangolare sarà:
$T_{n}=1+2+3+\ldots +n$
E qui ci viene in aiuto il signor Gauss, in barba al suo maestro elementare. Quanto fa questa somma?
Lo sappiamo:
$T_{n}=\dfrac{n\left( n+1\right) }{2}$
Ed ecco comparire l’algebra. La formula si può dimostrare usando le proprietà delle uguaglianze e il calcolo letterale.
Possiamo scrivere:
$T_{n}=1+2+3+\ldots + \left( n-2\right) +\left( n-1\right) +n$
Ma anche:
$T_{n}=n+ \left( n-1\right) +\left( n-2\right)+\ldots+3+2+1$
Ora sommiamo le due uguaglianze membro a membro e otteniamo:
$2T_{n}=\left( n+1\right)+\left( n+1\right)+\left( n+1\right)+…+\left( n+1\right)+\left( n+1\right)+\left( n+1\right)=n\left( n+1\right)$
$n$ volte
Da qui, dividendo per $2$, abbiamo:
$T_{n}=\dfrac{n\left( n+1\right) }{2}$
E Peano? Come dimostrerebbe lui questa formula? Ma per induzione, naturalmente!
- Vediamo se la proprietà è valida per $n=1$: $T_{1}=\dfrac{1\left( 1+1\right) }{2}$. In effetti $1$ è il primo numero triangolare.
- Facciamo ora il fatidico passo induttivo, prestando attenzione a non cadere: supponiamo che la proprietà sia valida per un certo valore di $n$ e dimostriamo che allora vale anche per il suo successivo $n+1$.
Dobbiamo dimostrare che è $T_{n+1}=\dfrac{\left( n+1\right)\left(n+2\right) }{2}$, sapendo che è $T_{n}=\dfrac{n\left(n+1\right) }{2}$.
Sappiamo pure che è $T_{n+1}=T_{n}+\left(n+1\right)$.
Quindi:
$T_{n+1}=\dfrac{n\left( n+1\right) }{2}+\left( n+1\right)=\frac{n^2+n+2n+2}{2}=\frac{n^2+3n+2}{2}=\dfrac{\left( n+1\right) \left( n+2\right) }{2}$
È fatta! Abbiamo la dimostrazione anche per induzione.
Possiamo quindi dire di aver rappresentato la successione dei numeri naturali con il suo termine generale, ragionando sui “sassolini” e mettendo in gioco un po’ di calcolo con i polinomi.
Ma possiamo anche dare la rappresentazione ricorsiva della successione.
Il foglio di calcolo ci viene in aiuto e chiarisce molto bene come si può trovare un termine dal precedente.
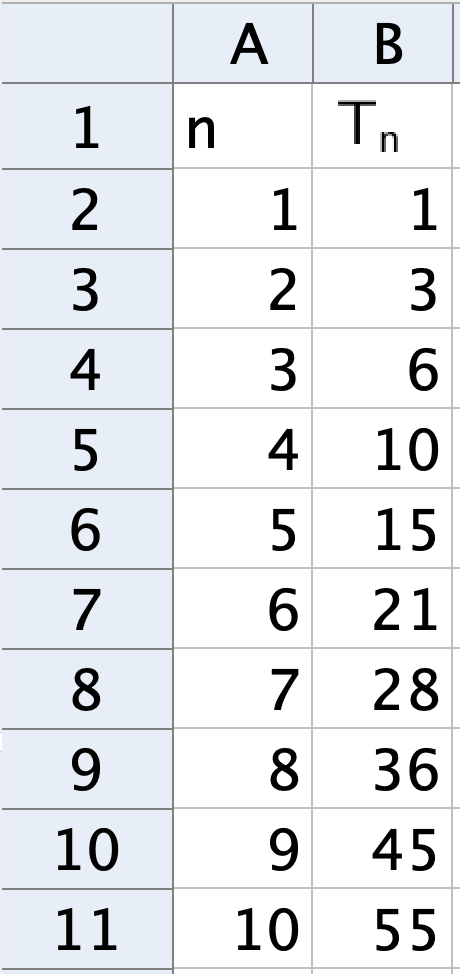
Come calcoliamo il generico numero triangolare $T_{n}$?
A parte il primo numero, $1$, ognuno degli altri si calcola prendendo quello che gli sta sopra e sommandogli il numero a sinistra, cioè $n$.
Nella cella B3, per esempio, dobbiamo scrivere: = B2+A3. Poi basta copiare e incollare.
Ma possiamo spingerci ancora oltre e vedere l’aspetto funzionale di tutta la questione.
Creando una lista di punti dalle coppie di numeri della tabella, possiamo tracciare il grafico della successione (figura 3): se poi abbiamo già gli strumenti, possiamo anche mostrare che i punti stanno su una parabola.
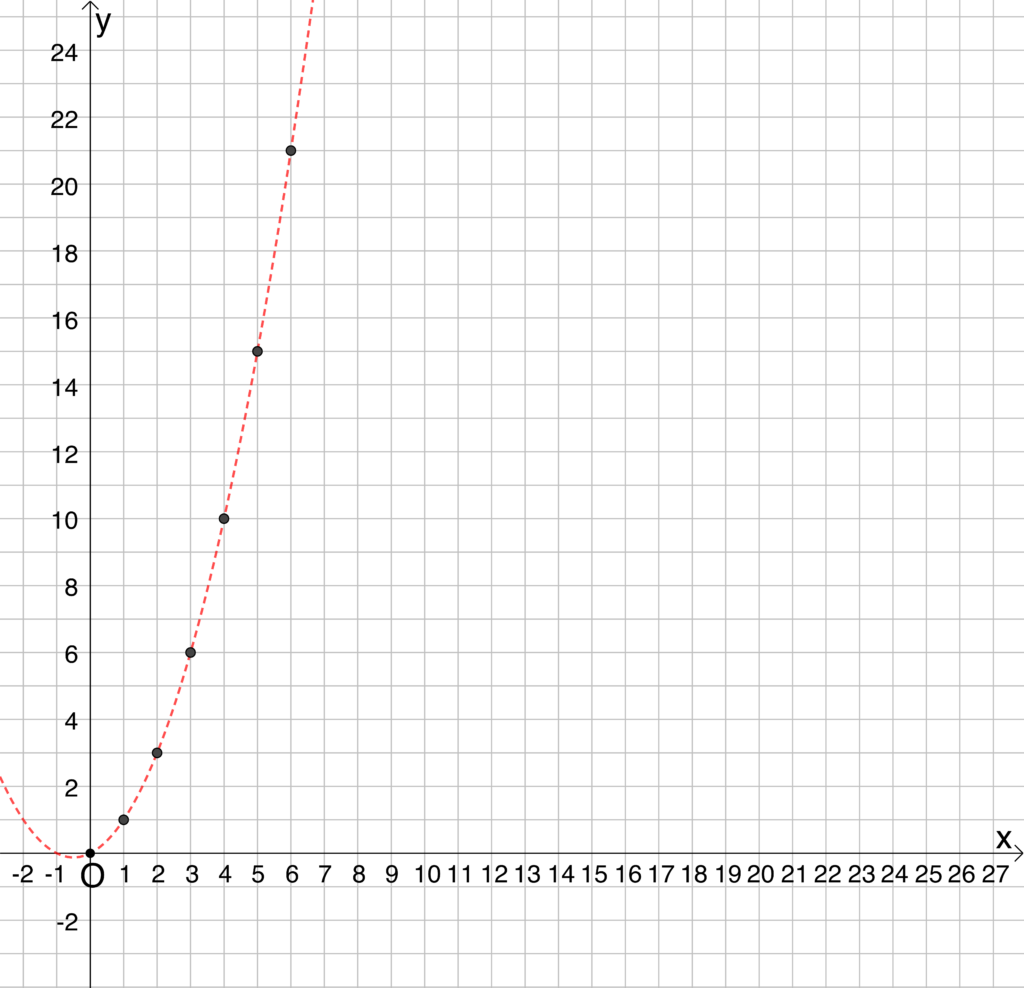
Riassumendo, i numeri triangolari possono accompagnarci negli anni: numeri, calcolo letterale, equazioni, successioni, funzioni…
Dopo ci sono i numeri quadrati, pentagonali eccetera. Non sto a rifare tutto il discorso, ma con i numeri quadrati è pure facile (figura 4).

Ragionando sui sassolini, si vede che, per trovare un numero quadrato, basta sommare al precedente un numero dispari:
$4=1+3$
$9=1+3+5$
$16=1+3+5+7$
Oh bella! Se sommiamo i numeri dispari tra loro otteniamo sempre un quadrato!
Rifacendo tutto possiamo dare:
- il termine generale della successione dei numeri quadrati $Q_{n}=n^{2}$:
- la rappresentazione ricorsiva $Q_{n+1}=Q_{n}+\left( 2n+1\right) $;
- il foglio elettronico e il grafico (che sempre parabola è – figura 5).
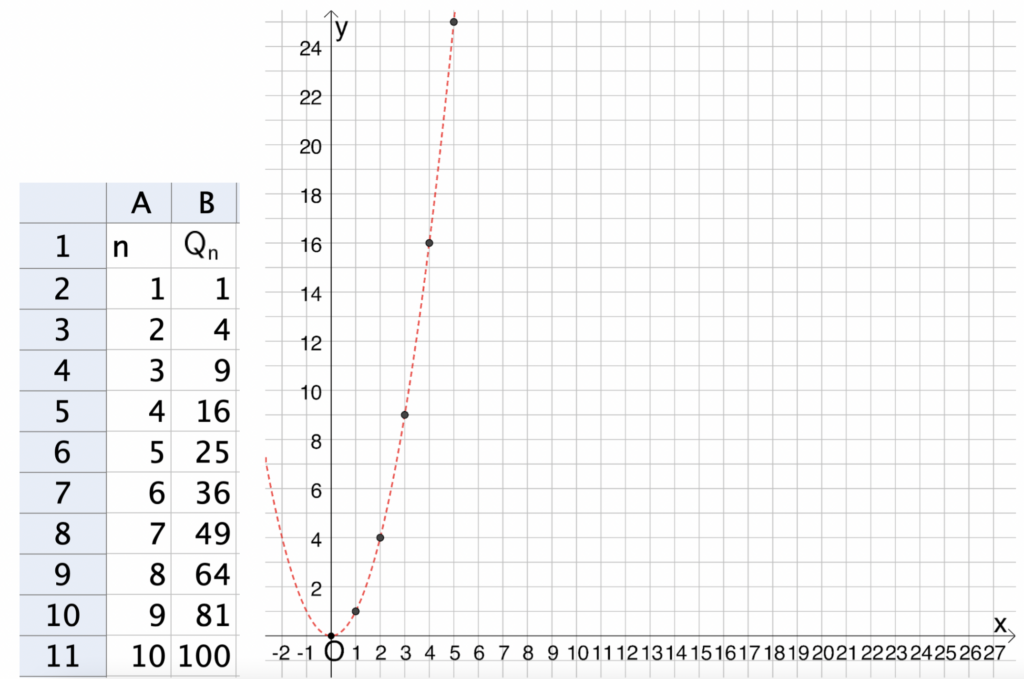
C’è pure una relazione tra numeri triangolari e numeri quadrati:
$Q_{n}=T_{n}+T_{n-1}$
che si può dimostrare alla Gauss e alla Peano; ma si può pure far vedere che una successione è data dalla somma di altre due e ragionare sui grafici e così via.

Sorvolo sui numeri pentagonali e tutti quelli che vengono dopo e vi propongo questo problema, che passa alla terza dimensione, introducendo i numeri piramidali.


Insomma, Antonio deve coordinare tutte le sue conoscenze sui numeri triangolari e quadrati: non è un mestiere semplice quello del pasticciere.
Queste attività sono tratte da “Nuova Matematica allo specchio edizione verde”, il nuovo corso di Matematica per il primo biennio edito da Ghisetti & Corvi.
