
In precedenti articoli abbiamo visto come piegare parabole ed ellissi tramite i loro inviluppi e abbiamo legato la piega alla descrizione della conica in coordinate. Non può allora mancare la terza famiglia di coniche: le iperboli. Anche in questo caso lo schema della lezione sarà lo stesso: piegheremo l’inviluppo delle tangenti dell’iperbole e successivamente passeremo alla descrizione analitica delle sue equazioni.
Gli studenti devono avere definito l’iperbole $\gamma$ come luogo dei punti per i quali è costante la differenza delle distanze da due punti fissi, ${F_1}$ e ${F_2}$, detti fuochi; in formula, fissato un numero reale positivo $r$, si ha:
$\gamma = \left\{ {P \in {\mathbb{R}^2}|\left| {{\rm{dist}}\left( {P,{F_1}} \right) – {\rm{dist}}\left( {P,{F_2}} \right)} \right| = r} \right\}$
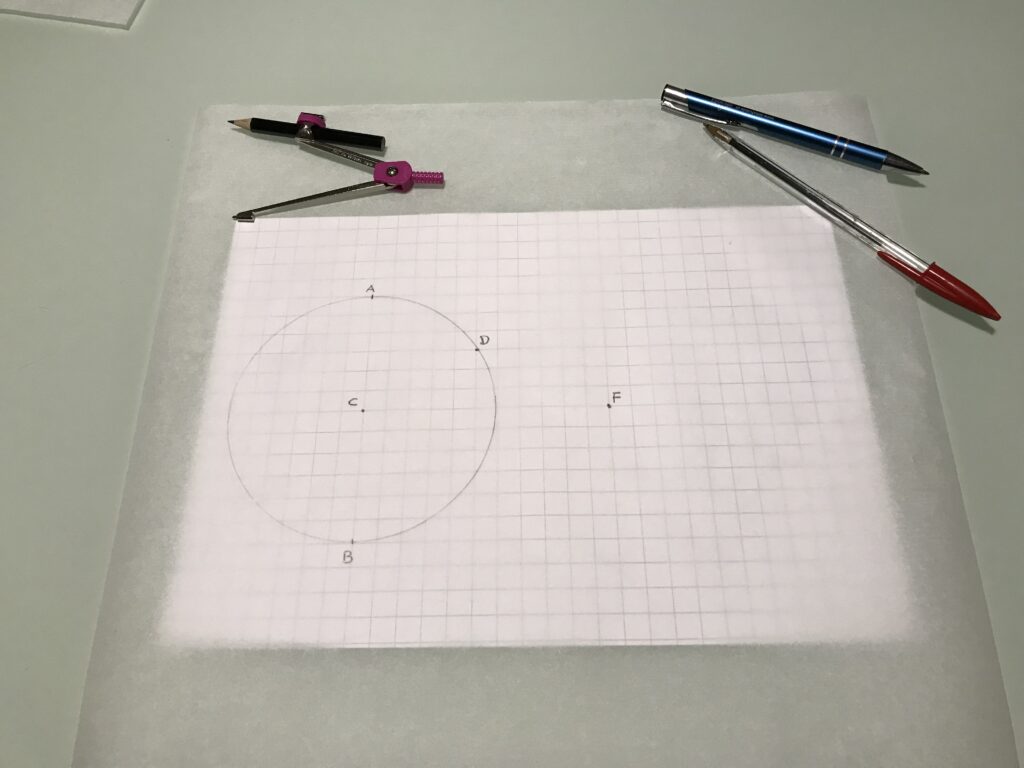
Per l’attività ogni studente avrà a disposizione un foglio di carta da forno (suggerisco di tagliarne dei quadrati con lato pari al lato corto del rotolo) e un foglio a quadretti dove appoggiare quello trasparente, come mostrato in Figura 1.

Pensando il foglio di carta da forno diviso in due dalla mediana del quadrato, ogni studente deve disegnare una circonferenza di raggio di circa $6$ cm in una delle due metà del foglio.
Se avete intenzione di trovare successivamente anche la descrizione algebrica dell’iperbole, invitate gli studenti a centrare il compasso nel vertice di un quadretto del foglio a quadretti. Fate poi fissare un altro punto $F$ nel vertice di un altro quadretto esterno alla circonferenza, come mostrato in Figura 2.

Per aiutarsi a centrare la figura sul foglio a quadretti, potete anche indicare i due punti del diametro perpendicolare alla retta congiungente $C$ con $F$, indicati con $A$ e $B$.
Diamo ora le istruzioni di piegatura.
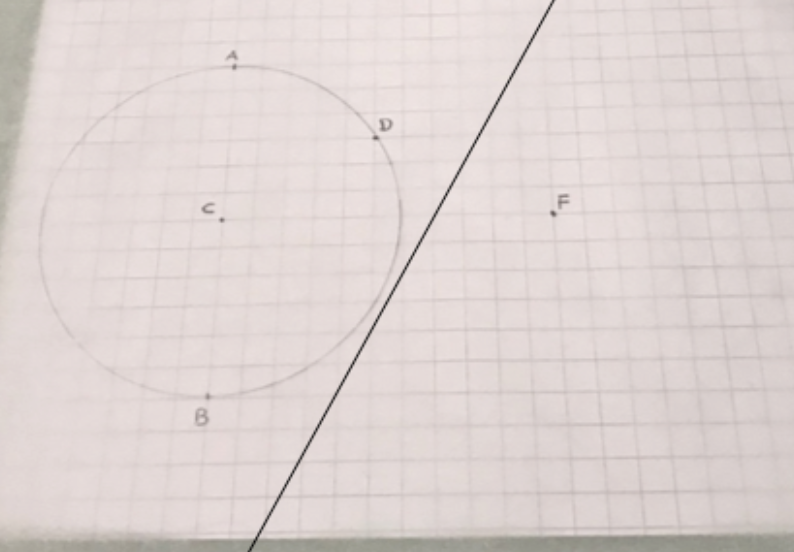

- Scegliere un punto $D$ sulla circonferenza stessa (Figura 3).
- Portare $D$ su $F$ piegando la carta e riaprire. Eventualmente ripassare la piega con la matita (Figura 4). Osservare che la piega è l’asse del segmento $DF$.
- Scegliere almeno un’altra quindicina di punti sulla circonferenza e piegare secondo l’istruzione data al punto precedente (Figura 5).
Cosa sembra apparire?
Le linee di piega si concentreranno tra $C$ ed $F$ e lasceranno libera una parte di piano ricordando un’iperbole. Possiamo mostrare che questo insieme di pieghe è effettivamente l’inviluppo delle tangenti a un’iperbole che ha fuochi in $C$
ed $F$, che corrispondono ai due fuochi chiamati ${F_1}$ e ${F_2}$ nella definizione.
Determiniamo infatti il punto della tangente che appartiene all’iperbole. Per farlo, analizziamo quello che succede quando si piega il punto $D$ su $F$.

In Figura 6, abbiamo ripassato in nero la retta $t$ piegata, che corrisponde alla tangente alla conica. Pieghiamo ora la retta passante per $C$ e per $D$; per semplicità possiamo disegnarla. Tale retta interseca $t$ in un punto $P$ che risulta il punto di tangenza all’iperbole. Infatti, $P$ appartiene alla piega, asse del segmento $DF$; quindi ${\rm{dist}}\left( {P,F} \right) = {\rm{dist}}\left( {P,D} \right)$. Ma, per come è stato costruito, abbiamo anche che $\left| {{\rm{dist}}\left( {P,F} \right) – {\rm{dist}}\left( {P,C} \right)} \right| = \left| {{\rm{dist}}\left( {P,D} \right) – {\rm{dist}}\left( {P,C} \right)} \right| = r$, raggio della circonferenza. Questo varrà per tutti i punti $P$ così costruiti che soddisferanno quindi la condizione $\left| {{\rm{dist}}\left( {P,F} \right) – {\rm{dist}}\left( {P,C} \right)} \right| = r$.
Osservazione 1
La costruzione dell’inviluppo permette di individuare in modo molto preciso alcuni elementi dell’iperbole: i vertici e gli asintoti. Infatti, i vertici si trovano portando $F$ sui punti del diametro che giace sulla retta per $C$ e $F$. Gli asintoti si ottengono in questo modo: tracciate le tangenti alla circonferenza uscenti da $F$ e indicate con ${T_1}$ e ${T_2}$ i punti di tangenza; piegate ora $F$ su ${T_1}$ e successivamente $F$ su ${T_2}$; le pieghe individueranno gli asintoti. Infatti, se ripetessimo il ragionamento della Figura 6 per ottenere il punto della piega che appartiene all’iperbole, dovremmo intersecare la retta $C{T_1}$ (rispettivamente $C{T_2}$) con l’asse di $F{T_1}$ (rispettivamente $F{T_2}$), ma queste sono parallele (perché?). La Figura 7 mostra vertici e asintoti.

Una domanda in più
Gli studenti possono riflettere sul fatto che i punti ${T_1}$ e ${T_2}$ di tangenza dividono la circonferenza in due archi. I punti di ogni arco danno luogo a un ramo dell’iperbole.
Osservazione 2
Si può accostare modello tangibile e virtuale mostrando, parallelamente alle pieghe tracciate, la costruzione geometrica ottenuta con GeoGebra.
Attività in coordinate
Potete proporre agli studenti di determinare l’equazione algebrica dell’iperbole che hanno piegato introducendo un opportuno sistema di riferimento. Per rendere più divertente questa seconda parte potete proporre di lavorare a coppie o in piccoli gruppi.
Gli studenti dovranno incollare il foglio di carta da forno sul foglio a quadretti che hanno inizialmente usato per fissare $C$ e $F$. Vi suggerisco di farlo aderire con il nastro adesivo lungo uno dei lati lunghi in modo che il foglio lucido sia parzialmente mobile.
Per ottenere l’iperbole in forma canonica, fate passare uno degli assi, per esempio l’asse delle ascisse, per i due fuochi ($C$ e $F$) e l’asse delle ordinate per il punto medio $O$ del segmento $CF$. La Figura 8 mostra in rosso il sistema da me scelto.

Relativamente al mio sistema si ha: $C\left( {\frac{-11}{2},0} \right)$ e $F\left( {\frac{11}{2},0} \right)$.
Per determinare l’equazione dell’iperbole possiamo procedere in due modi:
- applicare la definizione di iperbole come luogo di punti
- sfruttare la scelta del sistema di riferimento partendo dal fatto che l’iperbole avrà equazione del tipo:
$\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1$
In questo caso non è difficile ricavare ${a^2}$ e ${b^2}$. Infatti, ${a^2} = 9$ e, ricordando che ${b^2} = {c^2} – {a^2}$ con $2c = d\left( {F,C} \right)$ si ottiene l’equazione di $\gamma :85{x^2} – 36{y^2} = 765$.
