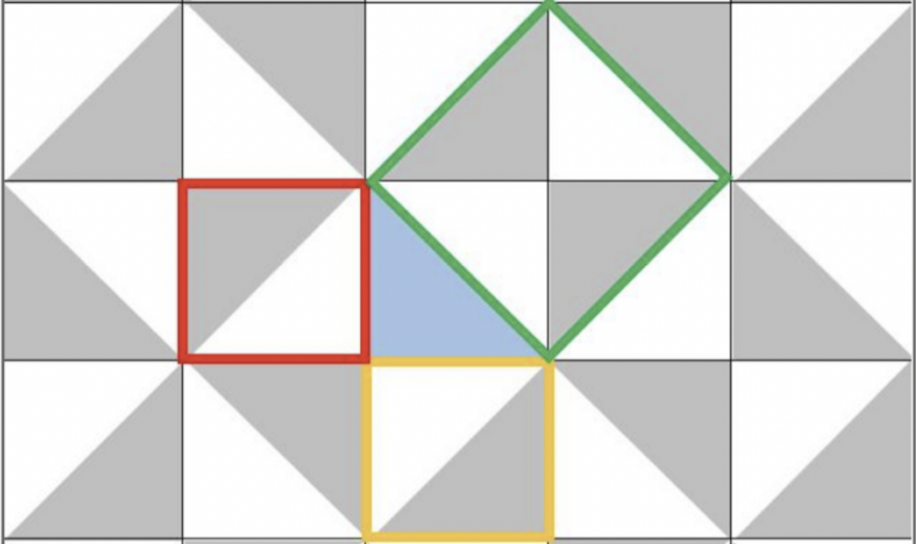
La leggenda narra che Pitagora ebbe l’intuizione per il suo famoso teorema durante una noiosa attesa passata a fissare un pavimento simile a questo, composto da piastrelle triangolari ottenute dalla metà di quadrati.

Osservando una qualsiasi di queste piastrelle, si nota che la pavimentazione stessa disegna su ciascuno dei tre lati un quadrato.
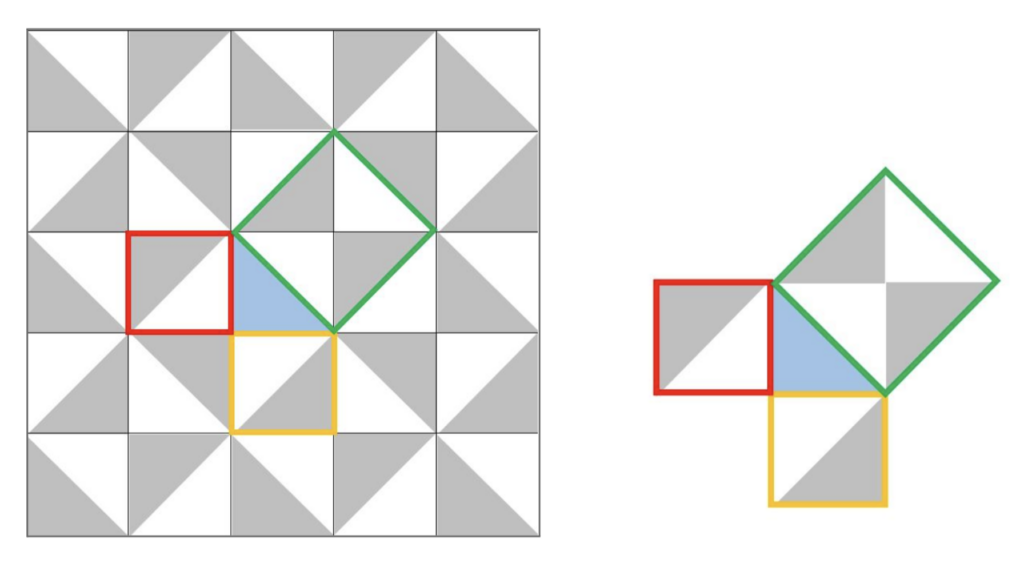
In particolare, i due quadrati costruiti sui cateti (quello giallo e quello rosso) sono entrambi costituiti da una piastrella scura e una chiara; mentre il quadrato costruito sull’ipotenusa (quello verde) contiene due piastrelle chiare e due scure, che sono proprio la somma dei due quadrati precedenti.
Possiamo provare a ricostruire questa situazione sulla quadrettatura dei quaderni e verificare empiricamente se questo tipo di relazione continua a valere per triangoli rettangoli isosceli di altre dimensioni.
Per farlo disegniamo un triangolo rettangolo con entrambi i cateti lunghi $4$ quadretti, tracciamo i tre quadrati e contiamo quanti quadretti sono contenuti in ciascuno, avendo cura di contare bene anche tutti i mezzi quadretti che troveremo in quello dell’ipotenusa.
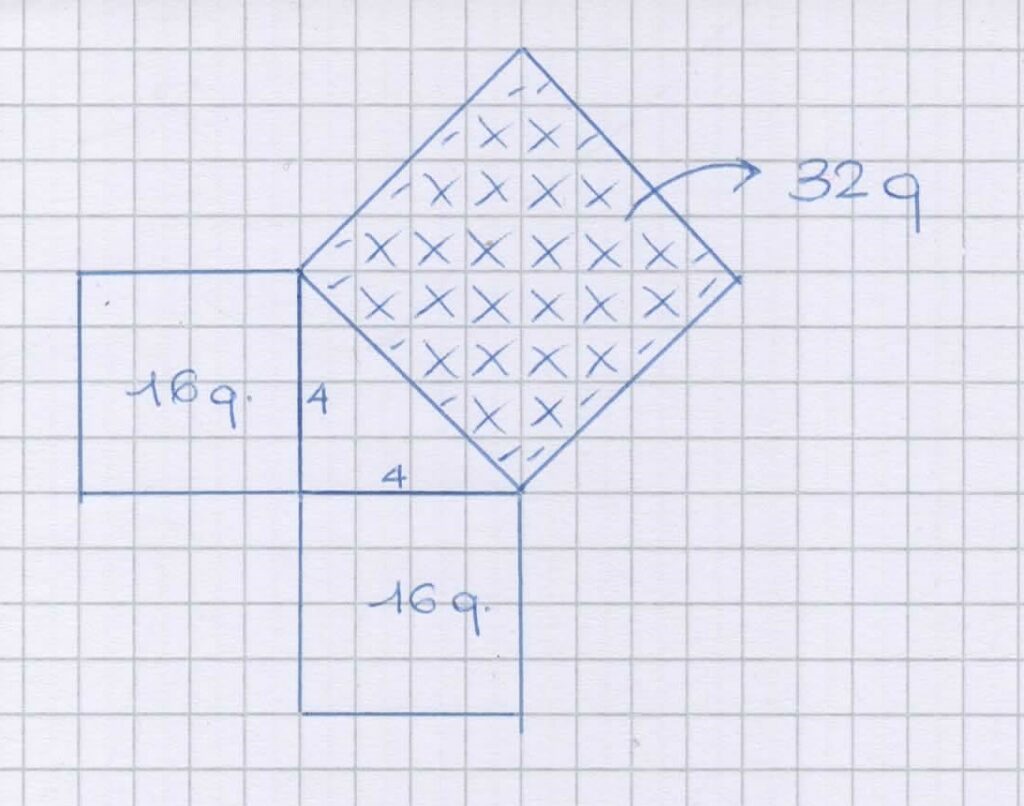
Verificato che vale per questo specifico triangolo, chiediamo alla classe di ripetere questo lavoro per triangoli rettangoli isosceli più grandi o più piccoli. Ben presto sarà chiaro che è valido per qualsiasi tentativo abbiano scelto di affrontare.
Viene quindi il momento di generalizzare ancora un po’: proponiamo di vedere se questa relazione resta valida per triangoli rettangoli qualsiasi.
In questo caso conviene lavorare in centimetri e seguire queste istruzioni:
- disegnare un triangolo rettangolo a piacere
- misurare con il righello tutti i lati e scrivere le misure sulla figura
- disegnare i tre quadrati e calcolare le loro aree
- controllare se la relazione di Pitagora è ancora valida
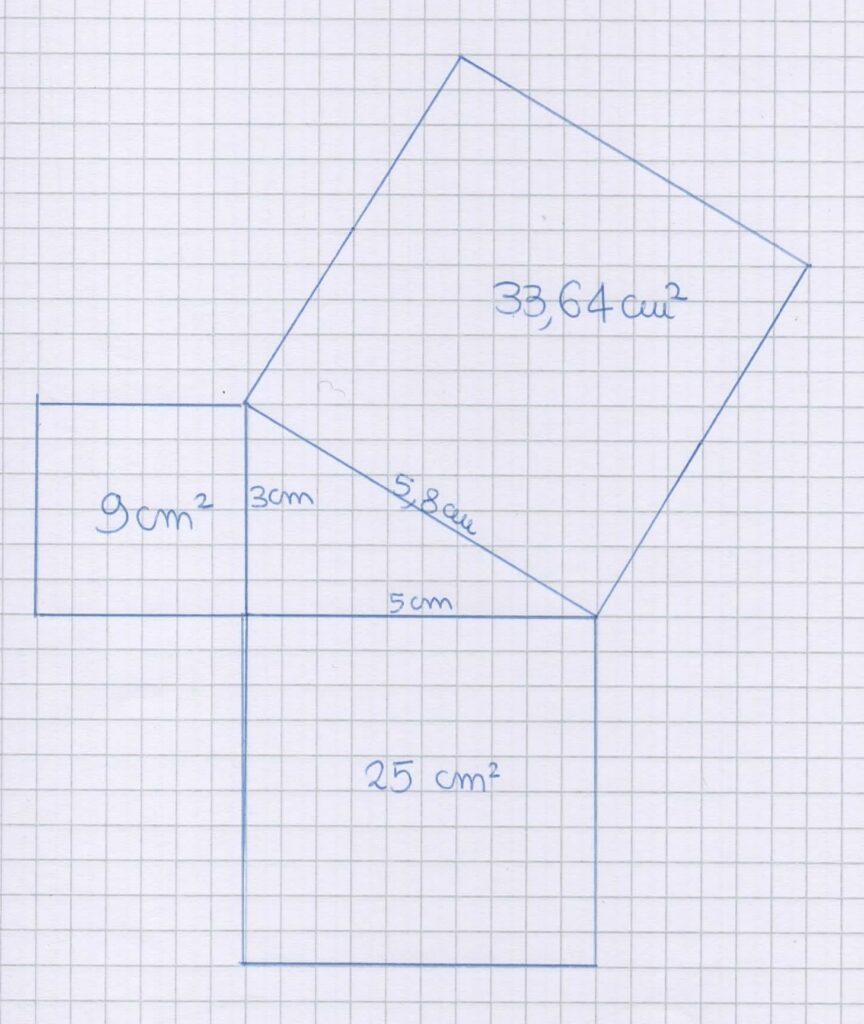
Si osserverà che non è semplice misurare in modo preciso l’ipotenusa e, nonostante si avvicini molto, difficilmente l’area del suo quadrato equivale esattamente alla somma degli altri due.
Questa è una buona occasione per riflettere sull’errore e per affidarci a uno strumento più preciso come GeoGebra. Basterà disegnare un triangolo rettangolo, costruire sui suoi lati i tre quadrati e inserire al loro interno la misura dell’area. Deformando a piacere il triangolo di partenza, si potrà osservare che la relazione di Pitagora continua a verificarsi.
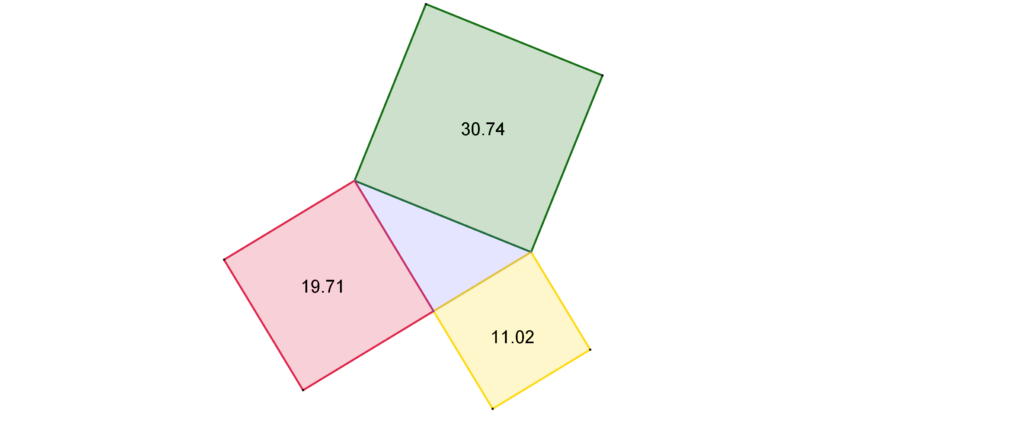
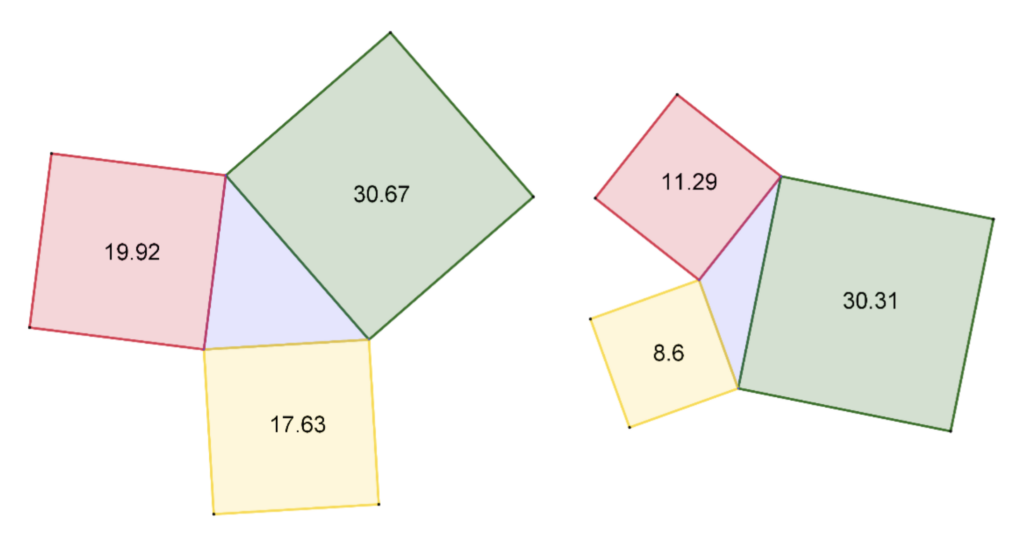
Non resta che provare sia su carta che su GeoGebra con dei triangoli scaleni ottusangoli o acutangoli per osservare con un certo disappunto che questa specie di magia smette di funzionare.
Naturalmente, questo lavoro di verifica non sostituisce una vera e propria dimostrazione, ma GeoGebra viene in nostro soccorso aiutandoci a generalizzare graficamente, per esempio con questa costruzione.
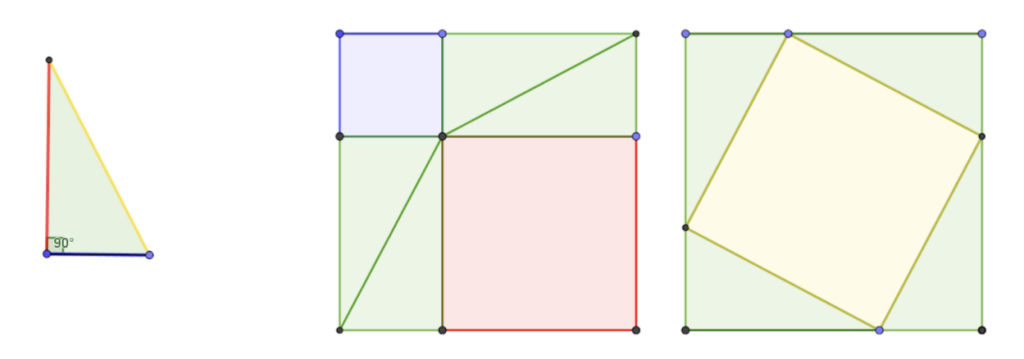
Partiamo da due quadratoni congruenti (il lato è la somma dei cateti) e al loro interno disegniamo quattro triangoli rettangoli congruenti a quelli di partenza in due modi diversi.
Se da due aree uguali si tolgono dei pezzi uguali le aree che avanzano sono uguali: nella prima figura l’area avanzata è la somma dei due quadrati costruiti sui cateti, nella seconda figura l’area avanzata è il quadrato costruito sull’ipotenusa, EUREKA!
Impostare l’azione didattica come scoperta permette alle classi di apprendere in un modo molto motivante. Vi assicuro che anche le alunne e gli alunni più insospettabili si sentiranno dei grandissimi geni vedendo che anche il loro triangolo rettangolo “funziona”; al contempo, il controesempio lascerà interdetti anche le alunne e gli alunni più sicuri di sé e delle proprie capacità matematiche. Entrambe queste reazioni porteranno spontaneamente i nostri ragazzi e le nostre ragazze a fare nuovi tentativi e a cercare un confronto con i compagni, generando una discussione significativa.
