Eccoci alle ultime settimane di scuola dove comincia a essere impegnativo coinvolgere gli studenti ormai vogliosi di meritate vacanze. Voglio allora proporvi un modo diverso di lavorare con le parabole che li impegnerà anche “manualmente”. Il prerequisito è che gli studenti abbiano definito la parabola ? come luogo dei punti equidistanti da un punto fisso F detto fuoco e da una retta d detta direttrice; in formula:
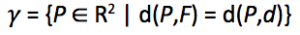
La prima parte dell’attività prevede la piegatura dell’inviluppo delle tangenti della parabola e alcune considerazioni di geometria sintetica; la seconda parte prevede invece di lavorare in coordinate, abbinando alla piegatura fatta l’equazione della parabola.
Distribuite a ogni studente un foglio di carta di dimensioni A4 o A5 (metà A4); se si vuole lavorare poi anche in coordinate meglio utilizzare carta quadrettata.
Cominciamo a “piegare” la parabola seguendo queste istruzioni che fanno riferimento alla figura 1:
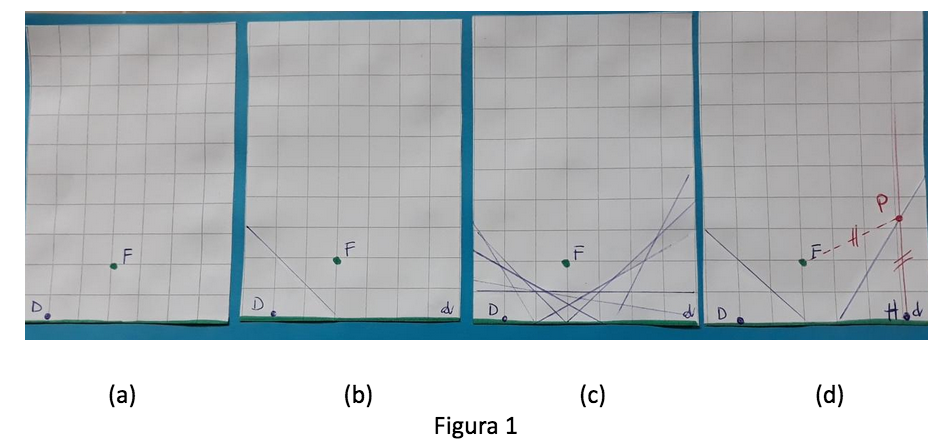
- Scegliere un punto F interno al foglio e un punto D su uno dei lati (d) del foglio stesso (fig. 1a).
- Portare D su F, piegando la carta, e riaprire. Eventualmente ripassare la piega con la matita (fig. 1b). Osservare che la piega è l’asse del segmento FD.
- Scegliere almeno un’altra decina di punti su d e piegare secondo le istruzioni date in 2 (fig. 1c).
Che cosa sembra apparire?
Agli studenti la traccia ricorderà una parabola. Fate però osservare agli studenti che hanno piegato rette (o porzioni di rette) mentre la parabola è una curva. Quello che hanno piegato è l’inviluppo delle tangenti a una parabola.
Possiamo determinare, per ciascuna tangente, il punto che appartiene alla parabola. Per farlo scegliamo un punto qualsiasi H appartenente a d, come in figura 1d, portiamo H su F, ottenendo la “piega tangente” come nel punto 2 e, successivamente, pieghiamo la retta perpendicolare a d e passante per H. Questa retta interseca la piega in P. Proprio P risulta il punto di tangenza alla parabola. Infatti P appartiene alla piega, asse del segmento HF; quindi d(P,F) = d(P,H). Ma, per come è stato costruito, abbiamo anche che d(P,H) = d(P,d). Quindi d(P,F) = d(P,d).
Osservazione: si possono accostare modello tangibile e virtuale mostrando, parallelamente alle pieghe tracciate, la costruzione geometrica ottenuta con GeoGebra.
Possiamo ora proporre agli studenti di fissare un sistema di riferimento e determinare le equazioni della parabola piegata. Per rendere più divertente questa seconda parte potete proporre di lavorare a coppie o in piccoli gruppi.
È interessante far scegliere agli studenti almeno due sistemi di riferimento diversi (in nero e rosso in figura 2), facendoli disegnare sul foglio a quadretti. La figura 2 mostra i due sistemi da me scelti.
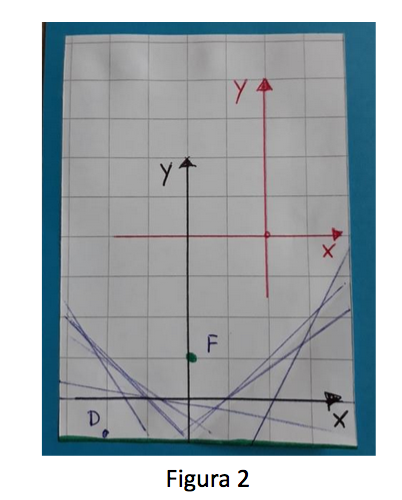
Per entrambi i sistemi di riferimento ho scelto il lato del quadretto della carta come unità di misura.
Nel sistema disegnato in nero, l’asse delle ordinate contiene il fuoco e l’asse delle ascisse passa per il vertice della parabola. Si ha dunque: F(0,1) e d: y = –1. Applicando la definizione di luogo di punti, dopo brevi conti si ottiene l’equazione di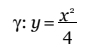 
Nel sistema disegnato in rosso si ha F(–2,–3) e d: y = –5. In questo caso l’equazione della parabola è
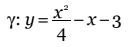
Questo esercizio permette di mostrare come lo stesso oggetto geometrico possa avere scritture differenti, di introdurre il concetto di forma canonica e di osservare alcuni invarianti della nostra parabola (per esempio, il coefficiente di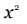 
legato all’apertura della parabola stessa).
Un’idea in più: gli studenti più coraggiosi possono cimentarsi nella scelta di un sistema di riferimento in cui nessuno dei due assi sia parallelo a d.