
Come è noto, le coniche non degeneri si suddividono in tre grandi famiglie: le parabole, le ellissi e le iperboli. In un precedente articolo vi ho proposto la piegatura della parabola tramite l’inviluppo delle tangenti e il suo successivo studio in coordinate. Proseguiamo allora con la costruzione origami dell’ellisse.
Il prerequisito è che gli studenti abbiano definito l’ellisse $\beta$ come luogo dei punti per i quali è costante la somma delle distanze da due punti fissi, ${F_1}$ e ${F_2}$, detti fuochi; in formula:
$\beta = \left\lbrace {P \in {\mathbb{R}^2}|{\text{dist} }\left( {P,{F_1}} \right) + {\text{dist}}\left( {P,{F_2}} \right) = r} \right\rbrace$
Analogamente a quanto fatto per la parabola, nella prima parte dell’attività vi propongo la piegatura dell’inviluppo delle tangenti dell’ellisse con considerazioni di geometria sintetica. Nella seconda parte vi suggerisco come lavorare in coordinate, abbinando alla piegatura fatta l’equazione dell’ellisse.
Ogni studente dovrà tracciare con il compasso, su carta a quadretti (meglio quella con quadretti da $1$ cm di lato), una circonferenza di raggio circa $6$ cm e ritagliare il cerchio per rendere più agevole la piegatura. Le istruzioni che darò nel seguito fanno riferimento alla Figura 1.




- Segnare il centro $C$ della circonferenza e un punto $F$ interno al cerchio. Scegliere poi un punto $D$ sulla circonferenza stessa (Figura 1(a)).
- Portare $D$ su $F$ piegando la carta e riaprire. Eventualmente ripassare la piega con la matita (Figura 1(b)). Osservare che la piega è l’asse del segmento $FD$.
- Scegliere almeno un’altra quindicina di punti sulla circonferenza e piegare secondo l’istruzione data al punto precedente (Figura 1(c)).
Cosa sembra apparire?
Le linee di piega limiteranno una regione ricordando un’ellisse. Possiamo mostrare che questo insieme di pieghe è effettivamente l’inviluppo delle tangenti a un’ellisse che ha fuochi in $C$ e in $F$, che corrispondono ai due fuochi chiamati ${F_1}$ e ${F_2}$ nella definizione.
Per mostrare questo, determiniamo il punto della tangente che appartiene all’ellisse. Analizziamo quello che succede quando si piega il punto $D$ su $F$. In Figura 1(d) ho ripassato in nero la linea $d$ piegata, che corrisponde alla tangente alla conica. Pieghiamo ora la retta passante per $C$ e per $D$ che lascerà come traccia il diametro per $D$. Per semplicità possiamo disegnare solo il raggio $CD$. Il raggio interseca $d$ in un punto $P$. Proprio $P$ risulta il punto di tangenza all’ellisse. Infatti $P$ appartiene alla piega, asse del segmento $DF$; quindi ${\rm{dist}}\left( {P,F} \right) = {\rm{dist}}\left( {P,D} \right)$. Ma, per come è stato costruito, abbiamo anche che ${\rm{dist}}\left( {P,C} \right) + {\rm{dist}}\left( {P,F} \right) = {\rm{dist}}\left( {P,C} \right) + {\rm{dist}}\left( {P,D} \right) = r$, raggio della circonferenza. Questo varrà per tutti i punti $P$ così costruiti che soddisferanno quindi la condizione ${\rm{dist}}\left( {P,C} \right) + {\rm{dist}}\left( {P,F} \right) = r$.
Si può accostare modello tangibile e modello virtuale mostrando, parallelamente alle pieghe tracciate, la costruzione geometrica ottenuta con GeoGebra.
Altri spunti di lavoro:
- Potete far tracciare l’ellisse di cui i ragazzi hanno piegato l’inviluppo con il metodo del giardiniere. Magari lavorando a coppie, gli studenti possono prendere un cordino lungo quanto il raggio della circonferenza. Uno studente terrà gli estremi in $C$ e $F$ e l’altro, tendendo il cordino, con l’aiuto di una matita traccerà l’ellisse. Questa attività riscuote sempre successo!
- Potete analizzare con gli studenti che cosa succede spostando $F$ all’interno del cerchio e ripetendo le istruzioni di piegatura. In particolare: che cosa succede se $F = C$? E se $F$ finisce sulla circonferenza? Nel primo caso, si otterrà l’inviluppo di una circonferenza concentrica alla precedente e di raggio $\frac{r}{2}$. Nel secondo caso, per la costruzione fatta che tiene fissa la somma $r$ delle distanze del punto dai fuochi, si otterrà solo il centro $C$ della circonferenza.
- Potete proporre agli studenti di determinare l’equazione algebrica dell’ellisse che hanno piegato introducendo un opportuno sistema di riferimento. Per rendere più divertente questa seconda parte potete proporre di lavorare a coppie o in piccoli gruppi. Inizialmente potete suggerire di fare passare uno degli assi, per esempio l’asse delle ascisse, per i due fuochi ($C$ e $F$) e l’asse delle ordinate per il punto medio $O$ del segmento $CF$. La Figura 2 mostra in verde il sistema da me scelto.
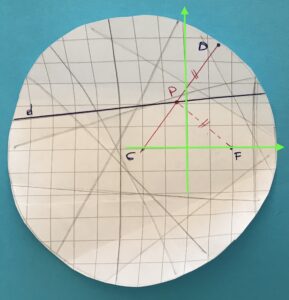
Relativamente al mio sistema si ha: $C\left( { – 2,0} \right)$ e $F\left( {2,0} \right)$ e $r = 6$. Applicando la definizione di luogo di punti, dopo brevi conti otteniamo l’equazione di $\beta :5{x^2} + 9{y^2} = 45$.
Si può ripetere l’esercizio con sistemi di riferimento differenti, scoprendo cosa resta invariato nell’equazione dell’ellisse.
