
Il gioco che vi propongo ha come obiettivo quello di ripassare il teorema di Pitagora, migliorando al tempo stesso la consapevolezza geometrica e la capacità di osservazione dei vostri studenti, che si dovranno confrontare con triangoli invisibili e distanze nascoste.
Dividete la classe in squadre (di tre o quattro studenti) e nominate un capitano per ogni squadra, che sarà l’unico studente della squadra autorizzato a muoversi per la classe. Proiettate sulla LIM una tavola di volo (per esempio quella mostrata in figura 1) e lanciate due dadi, comunicando agli studenti la coppia di valori ottenuti.
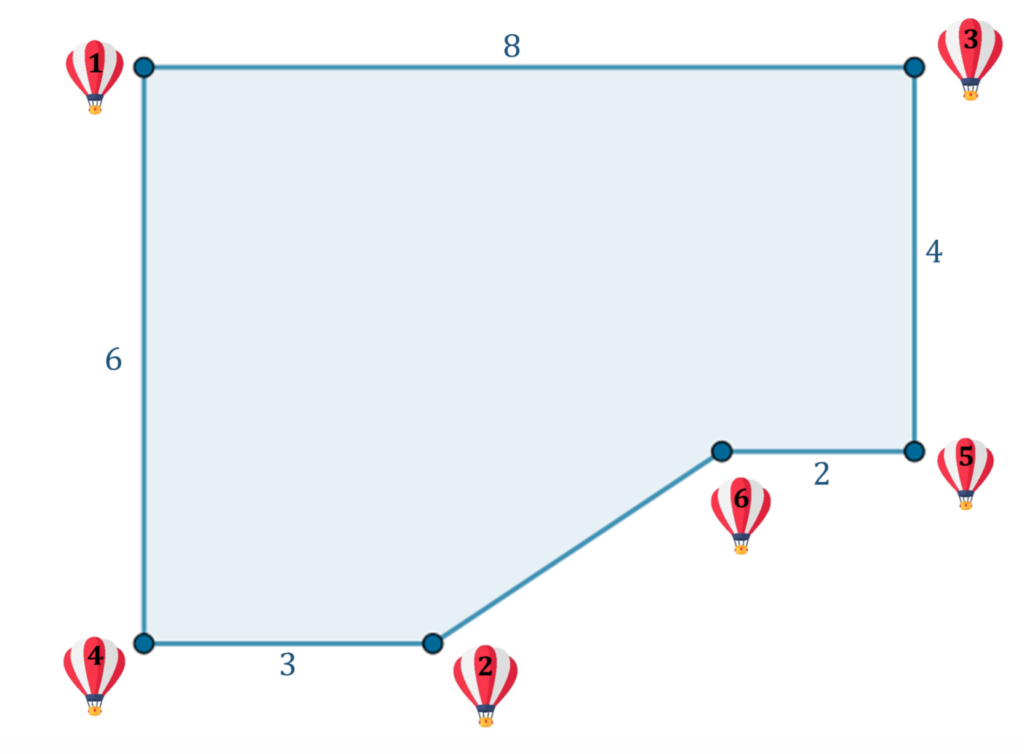
Lo scopo del gioco è quello di identificare nella tavola di volo la posizione delle due mongolfiere che corrispondono ai due numeri ottenuti con i dadi e calcolarne la distanza nel minor tempo possibile. Nel caso in cui, per calcolare la distanza, sia necessario utilizzare il teorema di Pitagora, sarà sufficiente indicare il risultato come la radice di un opportuno numero intero.
Quando la squadra ha calcolato la distanza tra le due mongolfiere, il capitano ne trascrive il valore su un foglietto che consegna all’insegnante. Il punteggio viene calcolato nel modo seguente: se la prima squadra che consegna ha indicato un valore corretto guadagna un punto, mentre in caso contrario gli viene tolto un punto. In questo secondo caso, l’insegnante procede a verificare i valori proposti dalle squadre che hanno consegnato dopo (seguendo l’ordine di consegna). Il punteggio viene assegnato come già spiegato e si procede in questo modo fino a quando si arriva a una squadra che ha dato la risposta corretta. A quel punto le consegne successive non vengono più considerate.
Una volta assegnato il punteggio il gioco procede cambiando tavola di volo e tirando nuovamente i dadi. Vince la squadra che alla fine della partita ha ottenuto il punteggio più alto.
Il gioco è stato progettato, oltre che per ripassare il teorema di Pitagora, per fare in modo che gli studenti imparino ad avvicinarsi ai problemi di geometria in maniera più critica e consapevole.
Per esempio, una volta identificate le due mongolfiere nella tavola di volo, è necessario che gli studenti riescano a vedere il triangolo rettangolo che ha come ipotenusa il segmento che le unisce (come in figura 2, in cui i valori ottenuti lanciando i dadi sono $4$ e $6$).
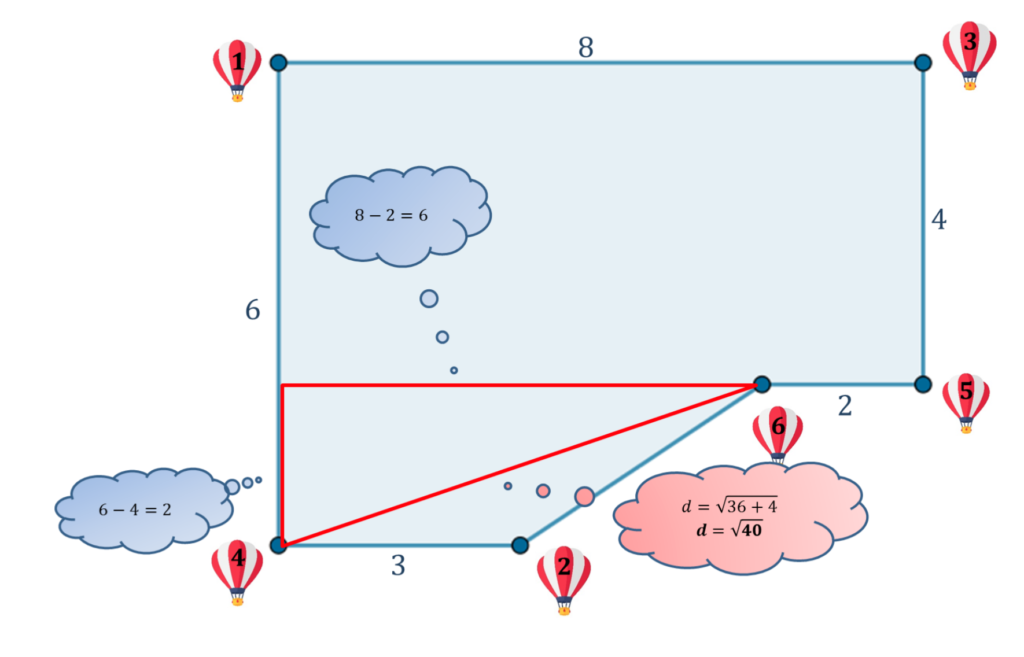
Nel caso in cui questa operazione risultasse troppo difficile per alcuni studenti, è possibile aiutarli fornendo loro le stampe delle tavole di volo insieme a degli stuzzicadenti, da utilizzare per visualizzare i triangoli in maniera tangibile.
Inoltre, le mongolfiere sono state posizionate in modo tale che le misure di alcuni segmenti non siano indicate esplicitamente, ma debbano essere ricavate osservando con attenzione la figura. Questo fa sì che lo studente impari, prima di affrontare un problema di geometria, a guardare con attenzione la figura, ricavando da essa il maggior numero possibile di informazioni.
Infine, il fatto di prevedere una penalizzazione per le risposte errate responsabilizza gli studenti, i quali saranno stimolati a riflettere e a discutere con i compagni di squadra prima di proporre la propria soluzione all’insegnante. In particolare, la scelta di premiare anche le consegne successive (in caso di errore nella prima consegna) spinge gli studenti a riflettere sulla gestione del tempo. Meglio prendersi qualche minuto in più ma consegnare una risposta corretta piuttosto che consegnare per primi rischiando di sbagliare!
In Zona Matematica, nell’area dedicata al gioco, potete trovare le tavole di volo e le soluzioni.
Vai all’area “Gioco” del I grado
Vai all’area “Gioco” del II grado – I biennio
