Questa settimana abbiamo lavorato in modo creativo sul teorema di Pitagora.

Dopo aver mostrato manualmente, con i cartoncini colorati come si può vedere in queste fotografie, che la somma dei quadrati costruiti sui cateti di un triangolo rettangolo è equivalente al quadrato costruito sull’ipotenusa, siamo passati a chiederci in quali situazioni nei contesti quotidiani è necessario conoscere il Teorema di Pitagora.
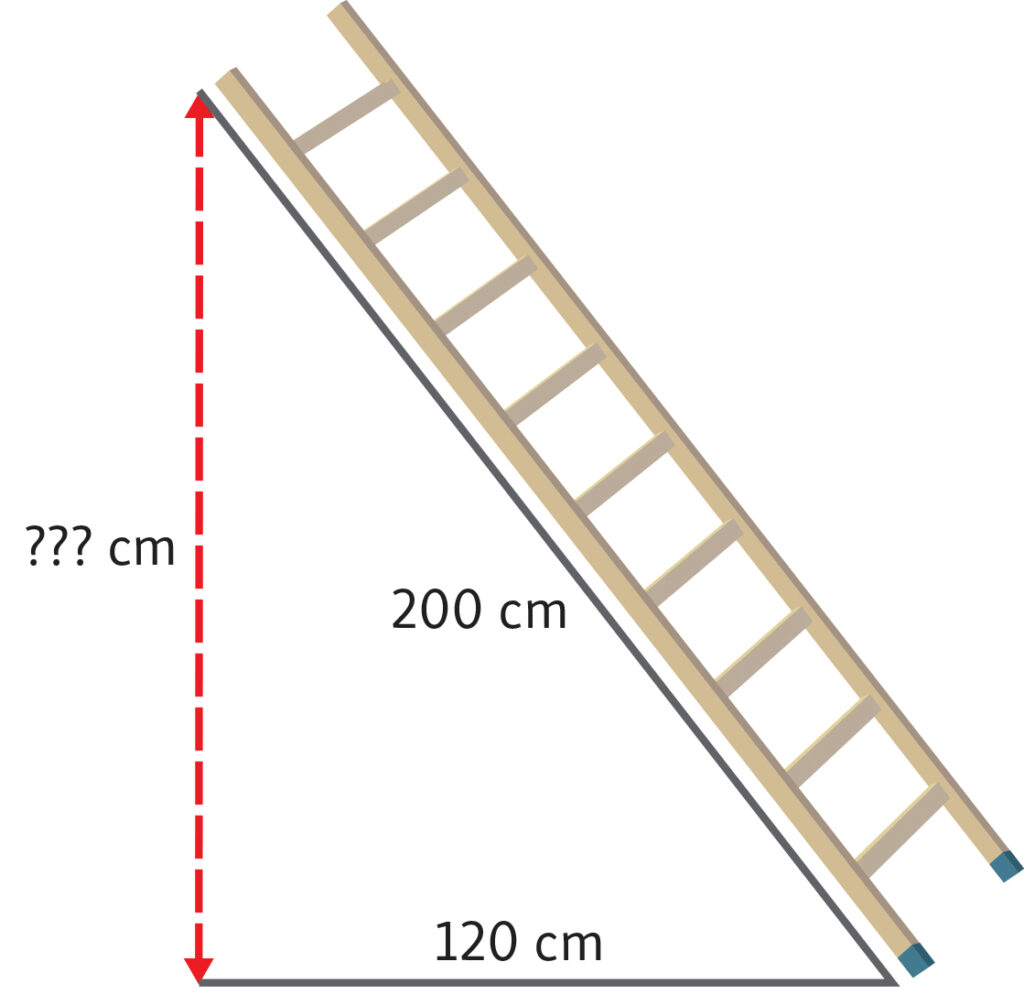
Osservando ciò che succedeva attorno a noi, abbiamo individuato un operaio che saliva su una scala appoggiata al muro. La scala rappresenta l’ipotenusa di un triangolo rettangolo con i cateti posti sul muro e sul pavimento e quindi ci siamo chiesti a che altezza la scala può essere appoggiata al muro, dato il punto in cui viene poggiata sul pavimento.

Sempre pensando alle scale, un alunno ha proposto la scala doppia, che può essere considerata il modello di un triangolo isoscele nel quale tracciare l’altezza che lo divide in due triangoli rettangoli. Quindi è possibile calcolare l’altezza a cui arriva la scala aperta conoscendo la sua lunghezza da chiusa e lo spazio tra i piedi quando è aperta.
Alcuni alunni hanno individuato triangoli rettangoli nei tiranti che reggono pali molto alti, in particolare uno studente ha descritto la sua antenna televisiva sul tetto, che era stata fissata con molti tiranti perché potesse raggiungere un’altezza sufficiente a consentire una migliore ricezione del segnale.
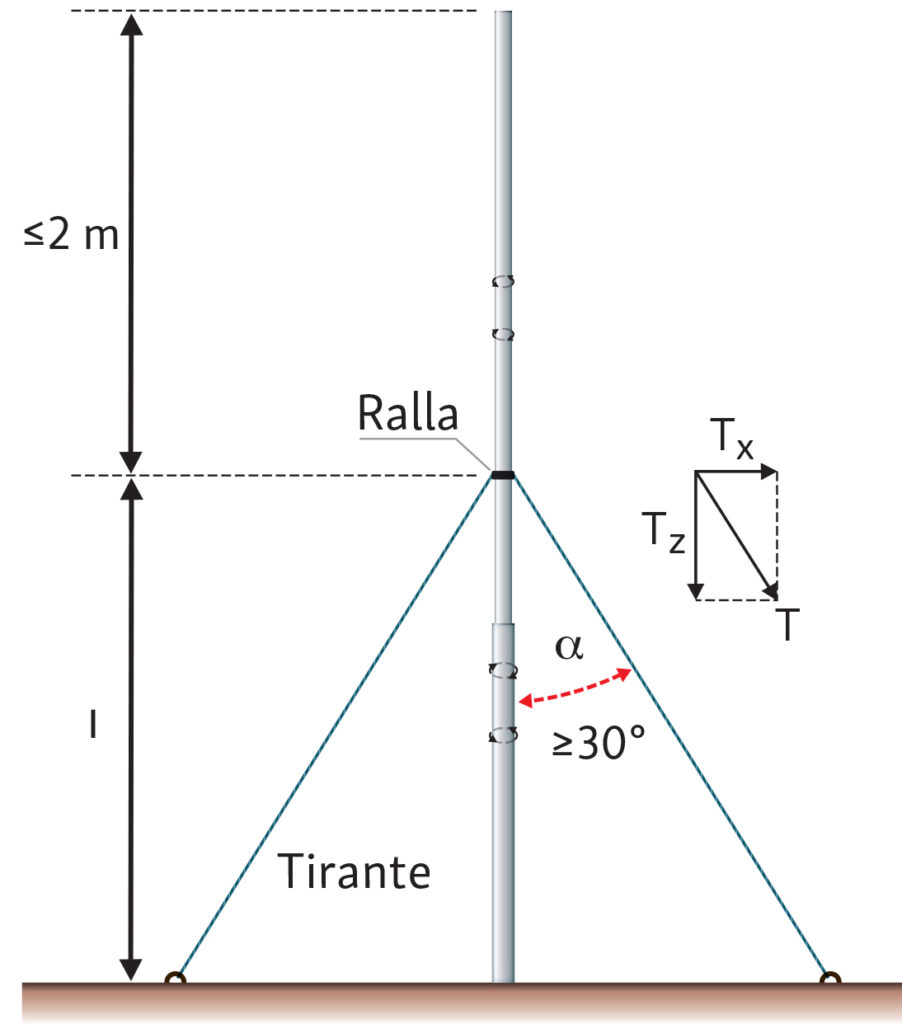
Cercando in rete una modellizzazione che permettesse a tutta la classe di interpretare nel modo corretto la situazione, abbiamo riconosciuto la particolarità della presenza nel triangolo rettangolo di un angolo acuto di $30^{\circ}$. Questo ci ha permesso di utilizzare le regole studiate per i triangoli rettangoli ottenuti dalla metà di un triangolo equilatero e quindi di utilizzare l’operazione di estrazione di radice.
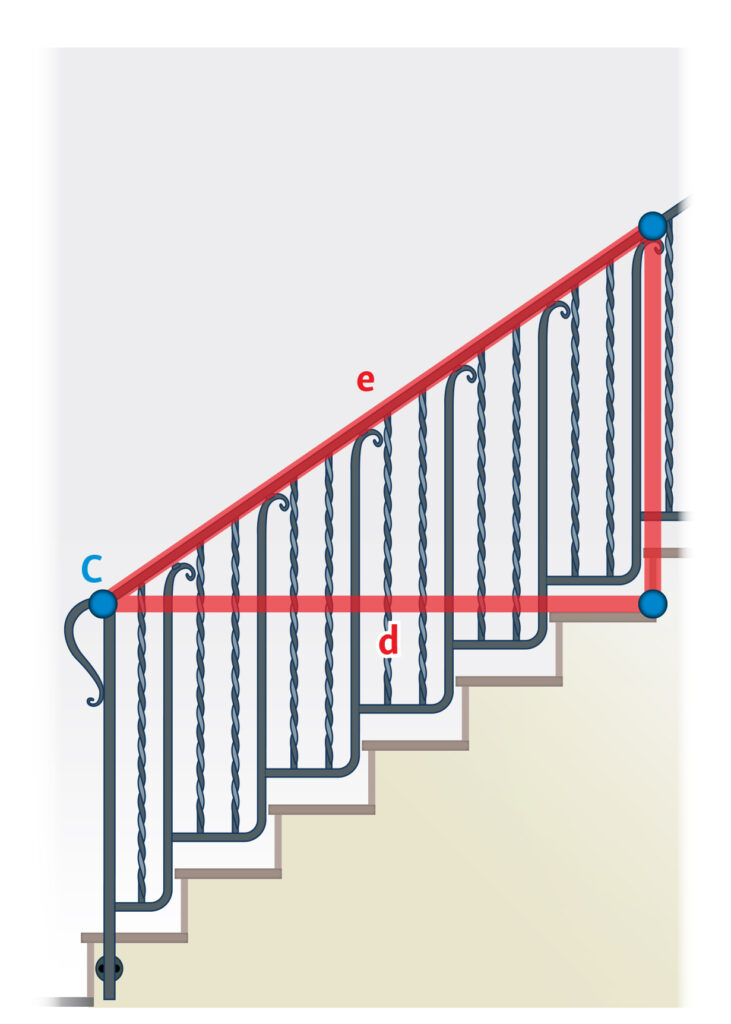
Un alunno, osservando le scale interne all’edificio scolastico, ha proposto di misurare la lunghezza del corrimano e la sua altezza da terra per calcolare la lunghezza della scala e, contando il numero dei gradini, determinare la misura della “pedata” di ciascun gradino.
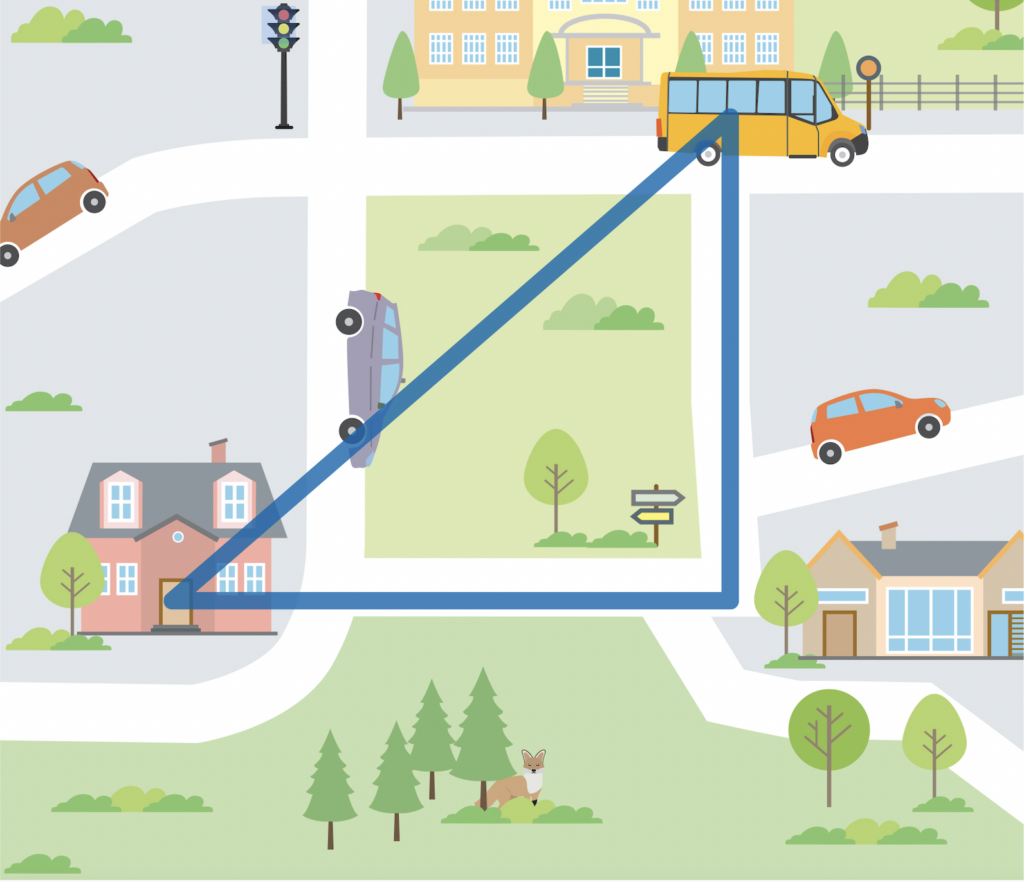
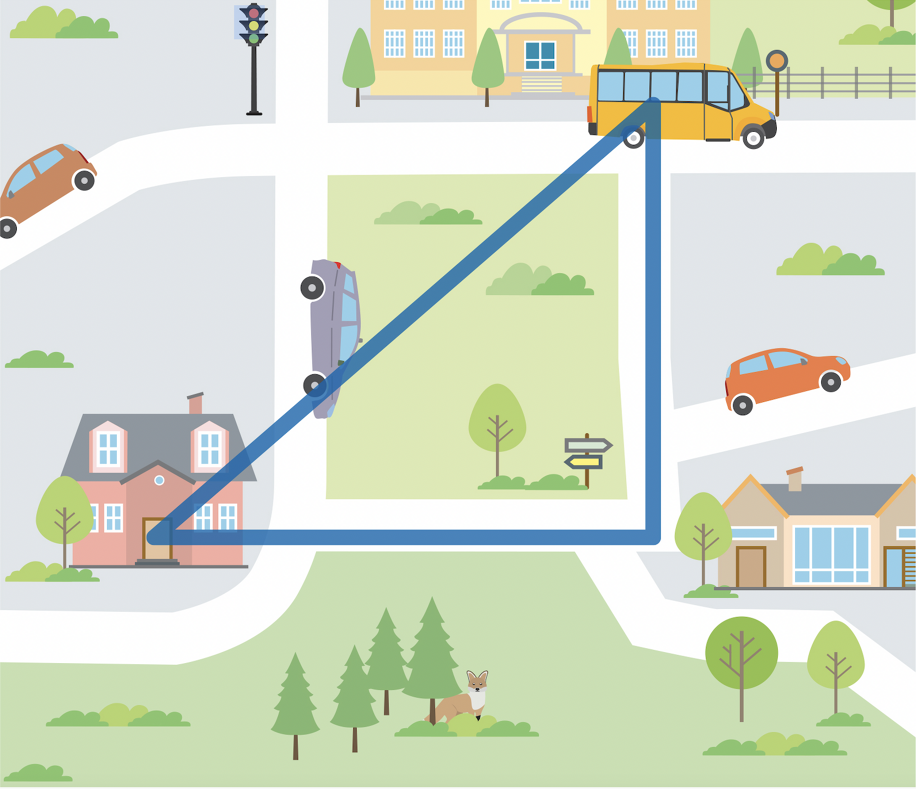
Altri ragazzi, guardandosi intorno in aula, hanno pensato alle carte geografiche e hanno semplificato la situazione utilizzando la geometria: determinare la distanza in linea d’aria tra la casa e la fermata del bus rispetto al percorso fatto abitualmente in cui è necessario passare sui marciapiedi che costeggiano le strade.

Qualcuno ha pensato alle mensole della propria stanza e ha scoperto che le staffe che le reggono hanno proprio la forma di un triangolo rettangolo.
Abbiamo proseguito la nostra ricerca pensando di dover appendere un festone con gli auguri di compleanno sulla diagonale del soffitto della stanza. Per determinare la lunghezza minima dell’addobbo è necessario conoscere le dimensioni del soffitto e utilizzare le lunghezze dei lati per determinare la misura della diagonale.
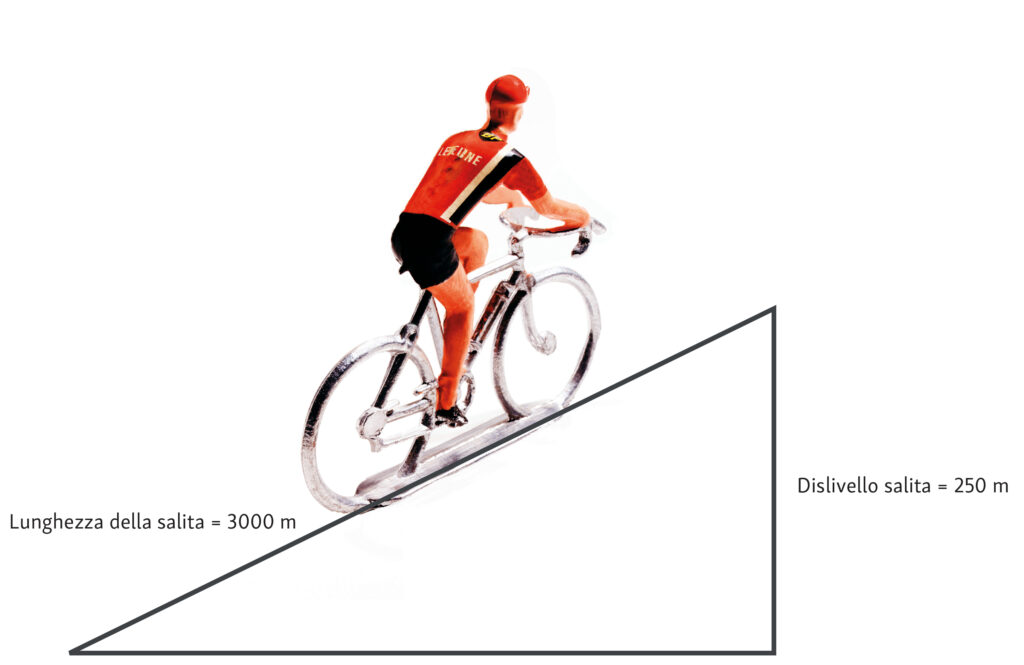
Infine, un ragazzo appassionato di bicicletta ha posto la seguente domanda: “Io per allenarmi percorro abitualmente una salita lunga $3000$ m con un dislivello di $250$ m, so che la pendenza delle salite viene espressa in percentuale, come posso fare per calcolare la pendenza di quella salita? Il teorema di Pitagora mi può aiutare?”
Per rispondere abbiamo schematizzato la situazione costruendo un triangolo rettangolo in cui l’ipotenusa corrisponde alla lunghezza della salita percorsa in bicicletta e il cateto minore corrisponde al dislivello della salita. La pendenza in percentuale corrisponde al rapporto fra il cateto minore e il maggiore del nostro triangolo e pertanto è necessario utilizzare il teorema di Pitagora per determinare la lunghezza del cateto maggiore.
Cercare i triangoli rettangoli che possiamo incontrare nel quotidiano è stato importante perché ha permesso, ancora una volta, di comprendere che la Matematica ha un riscontro nella realtà quotidiana e non sempre è necessario conoscere tutte le misure degli oggetti, ma alcune le possiamo calcolare!
