
Riuscire a creare un collegamento tra i programmi scolastici e le passioni degli studenti può essere un’ottima strategia per stimolare l’attenzione e l’interesse nei confronti di un argomento.
I videogiochi sono molto diffusi tra gli studenti della scuola secondaria e si può sfruttare questa passione per far capire come sotto al cofano di un qualsiasi videogioco ci sia molta matematica.
Immaginiamo esista un videogioco dal nome di fantasia Wizard Fight nel quale ciascun giocatore guida il proprio personaggio, un potente stregone, all’interno di un mondo virtuale combattendo contro gli altri giocatori a colpi di magie. In un gioco di questo tipo l’applicazione tiene traccia della posizione di tutti i giocatori sulla mappa tramite delle coordinate cartesiane. Ogni volta che un giocatore si sposta le coordinate vengono aggiornate come se il punto avesse effettuato una traslazione.
Ipotizziamo che un giocatore si trovi inizialmente nel punto (-5, 3) della mappa e che nel punto (4, 7) ci sia una pozione magica da raccogliere. Se il giocatore ha la possibilità di percorrere il tragitto più breve, dovrà effettuare una traslazione descritta dal vettore di componenti (9, 4) per raggiungere la pozione.
In Wizard Fight i diversi incantesimi utilizzabili in un duello hanno effetto solamente se l’avversario si trova entro una certa distanza. Quando un giocatore lancia un sortilegio l’applicazione, in base alla distanza tra i due personaggi e alla portata dell’incantesimo, deve stabilire se la magia avrà effetto o no. Immaginiamo per esempio che Alice si trovi nel punto (-20, -15) della mappa e Bruno si trovi nel punto (16, 12). Alice lancia un incantesimo che ha una portata di 50: riuscirà Alice a colpire Bruno?
Date le posizioni dei due giocatori si può calcolare la loro distanza tramite la formula della distanza:
Nel nostro caso il risultato del calcolo fornisce il valore di 45, per cui Bruno subirà gli effetti dell’incantesimo. Questi elementi si possono combinare tra loro per creare degli esercizi con traslazioni e calcoli di distanze ispirati all’ambientazione di un videogioco.
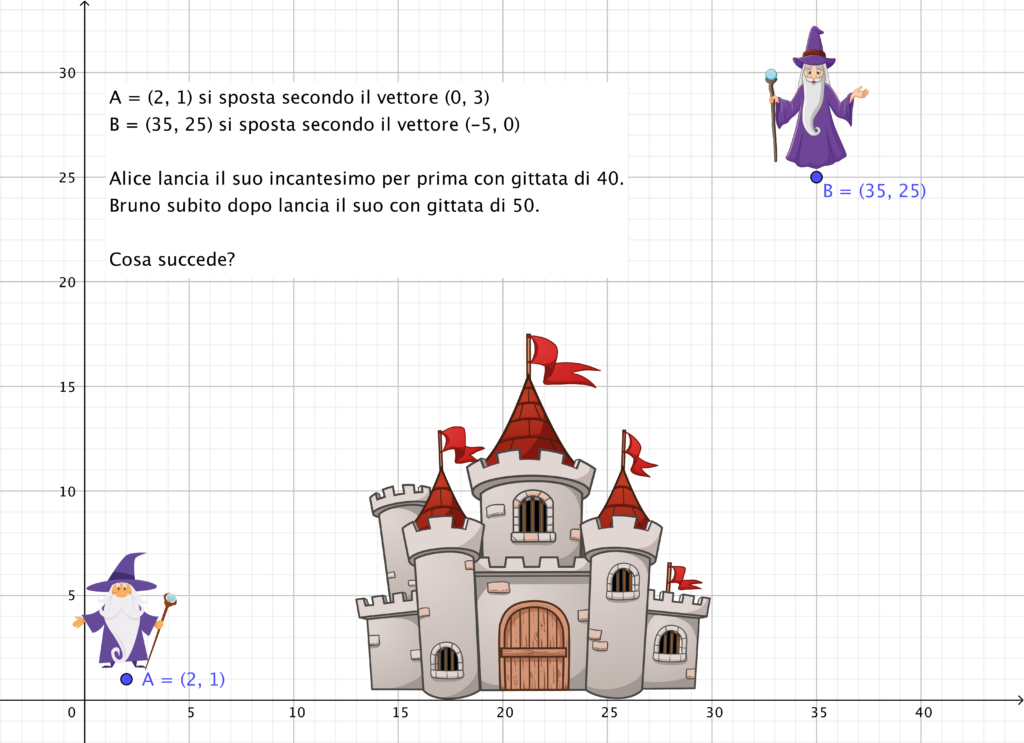
Per esempio, potreste proporre una situazione in cui Alice si trova nel punto (2, 1) e Bruno nel punto (35, 25) e non possono vedersi per la presenza di un castello. Entrambi i giocatori effettuano uno spostamento, Alice con una traslazione definita dal vettore (0, 3) e Bruno con una traslazione definita dal vettore (-5, 0).
A questo punto i due giocatori si vedono, Alice lancia un incantesimo che per Bruno sarebbe fatale e che ha portata di 40, Bruno cerca di rispondere con un altro incantesimo che ha portata di 50. Che esito avrà questo duello?
Ci sono tre possibili risultati:
- Se la distanza tra Alice e Bruno è minore di 40 allora Bruno verrà eliminato prima di riuscire a lanciare il suo incantesimo.
- Se la distanza tra Alice e Bruno è compresa tra 40 e 50 allora Bruno non subirà gli effetti della magia e riuscirà invece a colpire Alice.
- Se la distanza tra Alice e Bruno è maggiore di 50 allora nessuno dei due sortilegi andrà a segno.
Prendendo spunto da questo esempio ci si può sbizzarrire creando situazioni con più giocatori, oppure con ostacoli di diverso tipo da aggirare con diverse traslazioni, o anche inserendo delle probabilità che l’incantesimo abbia effetto o no.
