
Si avvicina la fine dell’anno scolastico, uno dei momenti più impegnativi per noi insegnanti: tocca tirare le somme del nostro lavoro, compilare una marea di scartoffie e pensare alle prove d’esame per le classi terze.
Ho dunque pensato di lanciarvi un “salvagente” proponendovi alcuni esercizi da sfruttare come simulazione in classe o da usare come spunto per costruire la “Prova di competenze logico-matematiche”.
Sono costruiti in modo da verificare l’acquisizione di conoscenze e abilità nei vari ambiti previsti dalla normativa, ma anche da poter dimostrare il livello di competenza raggiunto nell’affrontare situazioni realistiche e aperte, che si possono risolvere creativamente in tanti modi diversi.
Approfitto per augurarvi una buona sopravvivenza a queste ultime intensissime settimane di scuola. Teniamo duro, l’estate si avvicina e presto sentiremo la mancanza delle nostre caotiche e meravigliose classi!
ESERCIZIO 1 – Geometria solida
Il comitato genitori ha deciso di festeggiare la vittoria della squadra di calcio della scuola ai campionati studenteschi offrendo a $140$ alunni un buon gelato artigianale.
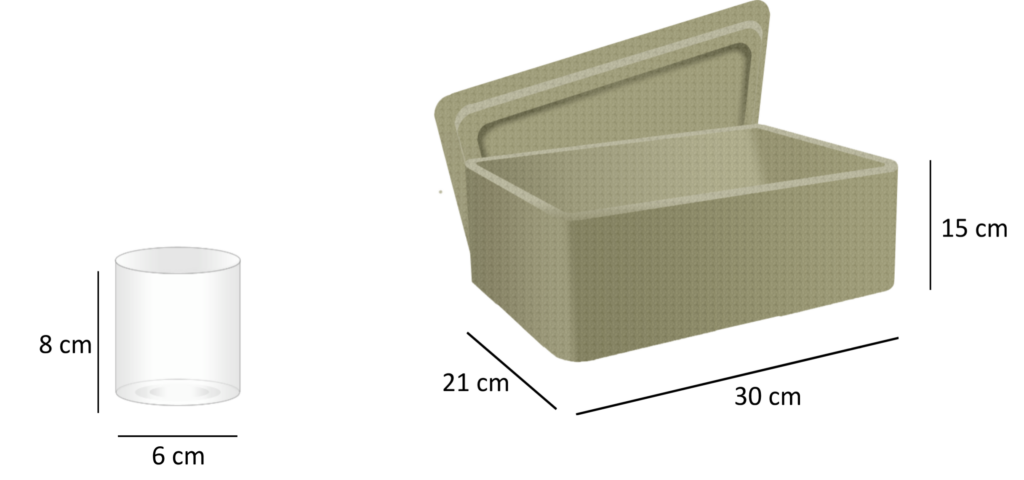
Il gelato viene acquistato in vaschette e servito in bicchieri come rappresentato nella figura.
- Quanti bicchieri si possono riempire con il contenuto di una vaschetta?
- Ogni vaschetta costa $80$ € e il comitato genitori ha a disposizione $250$ €, si riesce a comprare il gelato per tutti?
- Se non riescono, come potrebbero risolvere il problema?
ESERCIZIO 2 – Geometria nel piano cartesiano
Una famosa boy band vuole realizzare una coreografia particolare sul palcoscenico durante l’esecuzione di un brano. Il coreografo fornisce questa lista degli spostamenti:
- Partite dal punto $A\left( 4;6\right)$
- Indietreggiate di $11$ passi (punto $B$)
- Spostatevi a sinistra di $7$ passi (punto $C$)
- Avanzate di $4$ passi (punto $D$).
- Traccia il percorso immaginando sul palcoscenico un piano cartesiano con l’origine al centro. La freccia dell’asse $y$ indica la posizione del pubblico e i ragazzi si spostano tenendo il viso sempre rivolto in quella direzione.
- Scrivi le coordinate dei punti $B$, $C$, $D$.
- Descrivi l’istruzione che permetterà ai ragazzi di tornare direttamente al punto di partenza (quanti passi e in quale direzione).
- Sul palcoscenico è presente un grande pupazzo gonfiabile con la base quadrata di lato circa due passi centrato nel punto $P\left( -2;1\right)$. I ragazzi rischiano di andarci a sbattere nel loro percorso? Eventualmente trova una soluzione.
ESERCIZIO 3 – Numeri
Luisa è appassionata di fotografia analogica e sta organizzando un viaggio di dieci giorni in Islanda durante il quale ha intenzione di scattare almeno un centinaio di fotografie; quindi, deve procurarsi un buon numero di rullini e trova queste offerte:
- su “Tutto Fotografia”: rullini da $24$ pose a $4,50$ €, la spedizione costa 8 €
- su “Photo-Dettaglio”: rullini da $36$ pose a € $8,00$ €, la spedizione costa 7 €
Sulla base di queste informazioni:
- Quanti rullini dovrebbe comprare su “Tutto Fotografia”?
- Quanti rullini dovrebbe comprare su “Photo-Dettaglio”?
- Da quale sito le conviene comprarli?
Una volta tornata dal suo viaggio dovrà far sviluppare le sue pellicole; si fida del lavoro di due fotografi di sua conoscenza ai quali si è rivolta in passato:
- il fotografo vicino a casa ha ancora un laboratorio, chiede $1$ € a stampa, ma sopra le $100$ stampe ha il $30\%$ di sconto;
- il sito “Analogic” chiede $0,60$ € a stampa, ma in più ci sono le spese di spedizione di $7$ €.
Sulla base di queste informazioni:
4. dove le conviene stampare?
5. quanto ha speso in tutto per le sue fotografie finora?
Luisa sa che circa il $25\%$ delle fotografie che scatta poi non vengono bene e le deve scartare.
6. Quante fotografie belle le rimangono?
7. Quanto incide la spesa su ognuna?
ESERCIZIO 4 – Relazioni e funzioni
Alcuni ragazzi vogliono organizzare una vendita di biscotti per raccogliere fondi per le divise nuove della squadra di calcio. Prepareranno loro stessi delle belle confezioni con i colori della squadra, ma acquisteranno i biscotti già pronti, cosa per la quale hanno due possibilità:
- la pasticceria vicina al campo, che li vende a $3,00$ €/kg;
- la fabbrica di dolci del paese vicino, dove costano $2,50$ €/kg.
Per andare alla fabbrica però devono prendere il bus; il biglietto costa $2,00$ € ogni viaggio e per prenderli devono andare due ragazzi.
- Costruisci una tabella ponendo nella prima colonna le seguenti quantità di biscotti: $1$ kg, $5$ kg, $10$ kg, $15$ kg, $20$ kg; nella seconda colonna metti il prezzo della pasticceria e nella terza il prezzo della fabbrica (tieni conto anche del bus).
- Prepara un piano cartesiano in cui $x$ rappresenta la quantità di biscotti e $y$ il loro costo complessivo ($1$ quadretto $=2$ €).
- Usa i dati della tabella per tracciare le due rette corrispondenti ai costi della pasticceria ($p$) e della fabbrica ($f$).
- Le rette $p$ ed $f$ si incontrano in un punto, chiamalo $A$. Quali informazioni puoi ricavare osservandole?
ESERCIZIO 5 – Dati e previsioni
Arianna, Giorgio e Paola frequentano una scuola di equitazione con $18$ cavalli: $7$ sono arabi, $6$ sono Hannover e $5$ Quarter Horse. Per abituare gli allievi a cavalcare ogni cavallo, a ogni lezione viene fatta un’estrazione.
- Per ciascuna razza, calcola la probabilità di estrazione. Indica il risultato in frazione e in percentuale.
- Il mercoledì Arianna e Giorgio cavalcano alla stessa ora. Se Giorgio ha estratto un arabo, qual è la probabilità che Arianna estragga un Hannover?
- Paola arriva per la lezione successiva e non può estrarre gli stessi cavalli perché devono risposare. Qual è la probabilità che estragga anche lei un Hannover?
- Le estrazioni che i tre amici hanno fatto questo mercoledì influenzano quelle che faranno mercoledì prossimo?
- Un giorno Arianna cambia orario di lezione e sono già stati impiegati $5$ cavalli. La sua probabilità di estrarre un Quarter Horse è circa del $23\%$, quanti cavalli della stessa razza erano già stati estratti?
