
Durante l’estate è importante non dimenticarsi di quanto fatto durante l’anno e prendersi magari del tempo per un ripasso diverso che faccia gustare gli argomenti affrontati.
Ecco allora una proposta per l’estate: lasciate ai ragazzi il compito di piegare (più volte) un semplice modulo origami, il tradizionale modulo di Sonobe. Potete anche piegare tutti insieme un modulo durante una delle ultime lezioni, quando sarà sempre più difficile tenere desta l’attenzione con l’aria di vacanza che serpeggia nella classe. In questo modo gli studenti, con l’eventuale aiuto del diagramma, dovrebbero essere poi in grado di riprodurre il modello.
Utilizzerete la piegatura del modulo di Sonobe per “lanciare” quattro attività che potranno essere svolte in settimane diverse: le prime tre attività avranno come obiettivo il ripasso e l’ultima l’esplorazione e la scoperta matematica. Ovviamente potete anche scegliere di proporne solo alcune, essendo esse indipendenti, o di aggiungerne altre.
Le attività sono pensate per la secondaria di primo grado ma possono essere facilmente semplificate per la primaria o rielaborate per il biennio della secondaria di secondo grado.
I ragazzi dovranno avere a disposizione almeno $4$ fogli quadrati della stessa misura (circa $15$ cm di lato); per l’attività finale il numero può arrivare a $12$ (o anche $30$), a seconda del desiderio creativo dei ragazzi. Se non avete la possibilità di distribuire carta origami fate pure ritagliare fogli a quadretti da colorare eventualmente da una parte.
Ecco il diagramma di piegatura, con istruzioni relative agli ultimi passaggi. Se state usando fogli a quadretti, la piegatura inizia con l’eventuale parte bianca del foglio rivolta verso l’alto.
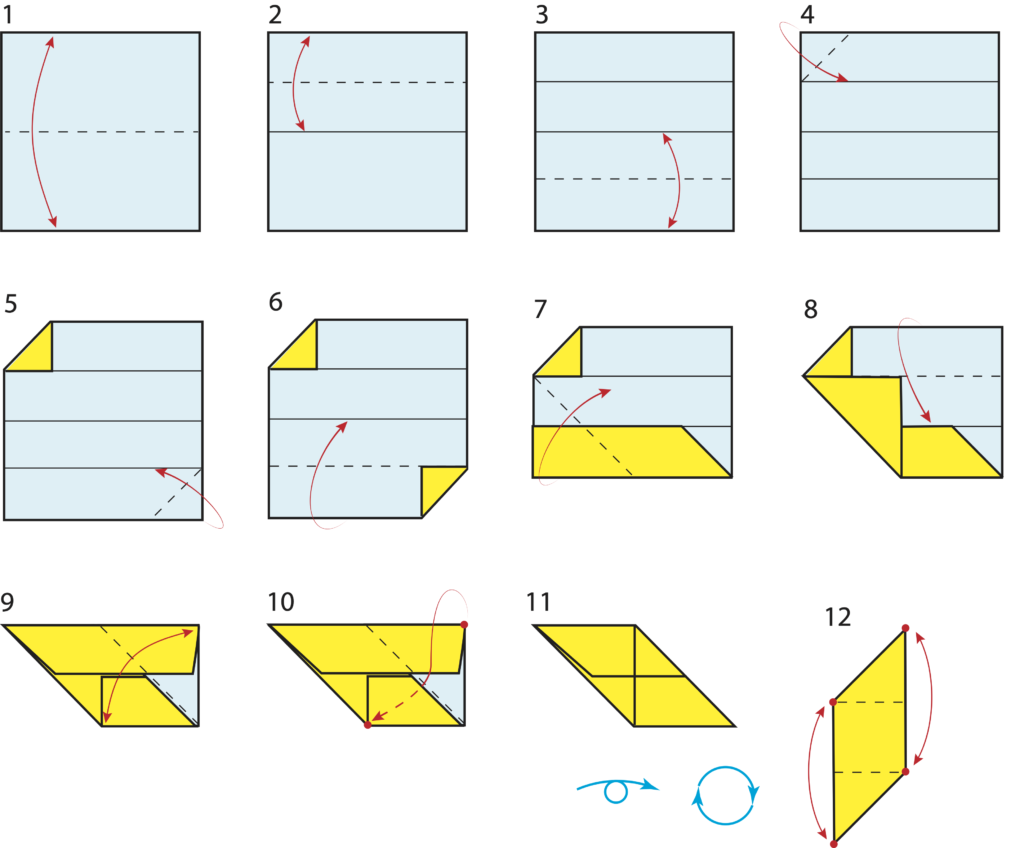
I passaggi fino al 6 non presentano particolari problemi; ecco le istruzioni per i passi successivi.
7. In questo passaggio, il lato bicolore a sinistra del pentagono va portato sul segmento dove poggia il cateto orizzontale del triangolo colorato in alto a sinistra.
8. Piega ora sul segmento orizzontale più lungo.
9. Porta il lato corto bicolore del trapezio rettangolo sulla base minore del trapezio stesso e riapri.
10. Ripiega la piega precedente, intascando sotto lo strato di carta colorato: si ottiene la figura 11. Ribalta ora la figura sul piano di appoggio.
11. La figura rappresenta un parallelogramma. Considerando ognuno dei lati più lunghi, porta un suo vertice sul suo vertice opposto, piega e riapri.
Ecco in breve le quattro attività che potete proporre. Trovate le schede pronte da assegnare in Zona Matematica.
_______________
Attività 1: riconoscere poligoni e descrivere alcune loro caratteristiche.
Obiettivo: utilizzare una corretta terminologia e precisione di linguaggio.
Nei vari passaggi di piegatura chiedete ai vostri studenti di descrivere la figura globale che si forma e le sue caratteristiche (quali, per esempio, eventuali centro e assi di simmetria). Chiedete anche di descrivere almeno una sua scomposizione in poligoni più semplici aiutandosi anche con quelli comparsi naturalmente con le pieghe.
Per esempio, nel passaggio 6 la figura è un esagono con due assi e un centro di simmetria. La figura può essere scomposta in due triangoli rettangoli isosceli e due coppie di rettangoli congruenti.
_______________
Attività 2: calcolare perimetri e aree.
Obiettivo: ripassare le formule per calcolare aree e perimetri di quadrilateri e triangoli e applicarle utilizzando la scomposizione di figure complesse in poligoni più semplici.
Alcuni consigli:
- potete qui scegliere, a seconda della classe e del lavoro che avete svolto in precedenza, di attribuire un valore numerico o simbolico (per esempio $a$) al lato $l$ del quadrato iniziale. Potrebbe essere comodo porre $l=4$ unità nel caso numerico;
- se la classe non conosce ancora $\sqrt{2}$, potete usare due misure di base: $a$ per il lato e $b$ per la misura della diagonale del quadrato (le altre diagonali che si formeranno saranno sottomultiple di questa).
Per esempio, la figura rappresentata nel passaggio 8 è un pentagono, di perimetro $2p$ e area $A$ dati rispettivamente da:
$2p=2\cdot \dfrac{3}{4}a+\dfrac{a}{2}+\dfrac{a}{2}\sqrt{2}+\dfrac{a}{4}\sqrt{2}$
$A=\dfrac{19}{32}a^{2}$
Per calcolare l’area ci sono tantissime modalità. Per esempio:
- si può vedere la figura come unione di due trapezi rettangoli, con la base maggiore comune (che poggia sul segmento tratteggiato in figura);
- si può considerare la figura come ottenuta dal rettangolo di lati $a$ e $\dfrac{3}{4}a$ meno le aree di due triangoli equivalenti a quelli disegnati in figura;
- si può prendere come unità di misura l’area del triangolino colorato più piccolo.
_______________
Attività 3: progettare un parco con il crease pattern (CP).
Obiettivo: risolvere problemi di realtà.
Per questa attività i ragazzi dovranno piegare fino a effettuare la piega del passaggio 9 e poi riaprire il modello. Lavoreranno sull’insieme (crease pattern) delle pieghe evidenziate.
Possono, se vogliono, colorare il loro CP, come nella seconda figura che segue, dove ho immaginato una strada che taglia un parco, con evidenziate due aiuole (i triangoli rettangoli isosceli), un bosco e un laghetto.


I problemi da risolvere sono: calcolare l’area della strada, delle aiuole, del bosco e del laghetto e progettare un nuovo parco.
_______________
Attività 4: sperimentare l’incastro dei moduli per creare differenti poliedri,
Obiettivo: sperimentare le proprie idee e dare spazio al creative thinking.
Per questa attività potete decidere se mostrare prima delle vacanze l’incastro fondamentale o dare semplicemente l’istruzione scritta (magari dicendo che in rete ci sono molti video sia di piegatura del modulo, sia della costruzione di poliedri).
I ragazzi potranno costruire vari poliedri e descriverli (numero di vertici, spigoli, facce). Eventualmente possono provare a valutare la superficie laterale.
_______________
Buone vacanze a tutti!
In Zona Matematica, nell’area dedicata agli origami, potete trovare i materiali di supporto all’attività.
Vai all’area “Origami” del I grado
Vai all’area “Origami” del II grado – I biennio
Vai all’area “Origami” del II grado – II biennio e V anno
