
La surfista non rimane a guardare il mare passivamente, come a volte le studentesse vivono la matematica procedurale, ma si immerge fra le onde, studiandone le potenzialità di elevazione e traslazione, potenzialità che cerca di padroneggiare, sfruttando le proprie personali capacità. Offriamo alle studentesse maggiori possibilità di conoscere queste capacità!
Il problema della Gender Inequalities in Matematica e in generale in ambito STEAM è certamente uno dei problemi più significativi nel contesto educativo italiano attuale, come ben sottolineato dagli ultimi risultati dell’indagine OCSE-PISA $2022$, che rivelano come in Italia sia stata registrata la differenza a favore del rendimento dei maschi più elevata in assoluto tra tutti gli $81$ Paesi partecipanti alla rilevazione.
I risultati fanno riflettere sugli stili di insegnamento e apprendimento della Matematica. Alcuni studi mettono in luce come le studentesse nell’individuare la risoluzione di un problema cerchino più dei maschi di ritrovare cosa è stato fatto in classe in situazioni simili e cosa l’insegnante si aspetti da loro. I problemi non standard sembrano quelli in cui le studentesse dimostrano maggiori difficoltà; inoltre, sembra che le femmine abbiano un maggiore livello di ansia matematica e una minore self-efficacy.
Forse anche la caratteristica di essere mediamente più riflessive dei maschi impatta negativamente sulla prestazione: spesso le femmine non hanno il tempo di completare tutti gli item richiesti dalla prova.
Per migliorare la situazione attuale, potrebbe forse aiutare quindi inserire nella pratica didattica più attività laboratoriali in cui si debbano risolvere problemi inusuali, problemi a più soluzioni o che, cambiando i dati, mostrino una soluzione ottimale diversa da quella utilizzata nella normale prassi didattica. Si potrebbe osservare mediante indicatori opportuni l’atteggiamento delle ragazze in situazioni più rilassate rispetto a una prova strutturata, a tempo, e vedere se i tempi di attivazione delle singole ragazze per iniziare a tentare una strategia risolutiva si riducono.
Oltre al problema della torta parzialmente ghiacciata proposto in un precedente articolo, vi propongo altri due semplici problemi che potrebbero favorire un’autonomia di pensiero matematico.
Il primo è un problema a risposta aperta che offre molteplici procedimenti risolutivi, fra cui anche quello algebrico dopo un’opportuna matematizzazione.
Devi spedire della cioccolata, delle biglie e alcune macchinine a Luca in un pacco che non deve pesare più di $1$ kg. La scatola per spedirlo pesa $80$ grammi, ogni biglia pesa $40$ gr, la tavoletta di cioccolata pesa $100$ g e ciascuna macchinina pesa $70$ g.
Come puoi riempire il pacco in modo che il suo peso si avvicini il più possibile a $1$ kg così da spedire a Luca più oggetti?
Il secondo problema si basa su situazioni problematiche che sembrano simili ma che vengono risolte con procedimenti ottimali diversi. Proporre queste situazioni in modo sequenziale rientra nelle tecniche per evitare il mindless-thinking.
Hai a disposizione dei contenitori non graduati $A$, $B$ e $C$ che pieni contengono rispettivamente $99$ dl, $23$ dl e $3$ dl. Hai acqua a volontà per riempirli. Puoi riempire un contenitore, svuotarne il contenuto in un altro, svuotare il contenuto per terra: puoi fare quello che vuoi. Alla fine devi ottenere un contenitore che contenga $70$ dl.
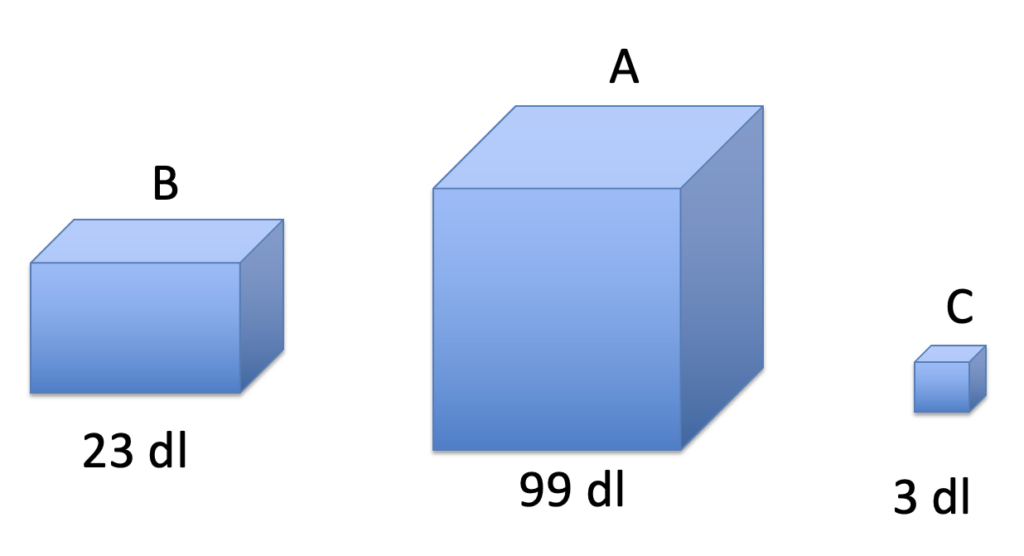
L’unico modo per esser certi che un secchio contenga esattamente $70$ dl è riempire completamente il contenitore $A$, svuotare poi parte del contenuto di $A$ nel contenitore $B$ fino a riempire quest’ultimo, versare poi parte dell’acqua contenuta in $A$ nel contenitore $C$, svuotare il contenitore $C$ (gettando l’acqua per terra) e riempire nuovamente $C$ con altri $3$ dl dal contenitore $A$:
$99$ dl $-23$ dl $-3$ dl $-3$ dl $=70$ dl
$A-B-2C$
Si ripropone poi la stessa situazione problematica variando le capacità dei secchi e la richiesta, in modo che comunque la strategia risolutiva sia sempre la stessa.
Hai a disposizione dei contenitori non graduati $A$, $B$ e $C$ che pieni contengono rispettivamente $169$ dl, $43$ dl e $3$ dl. Hai acqua a volontà per riempirli. Puoi riempire un contenitore, svuotarne il contenuto in un altro, svuotare il contenuto per terra: puoi fare quello che vuoi. Alla fine devi ottenere un contenitore che contenga $120$ dl.
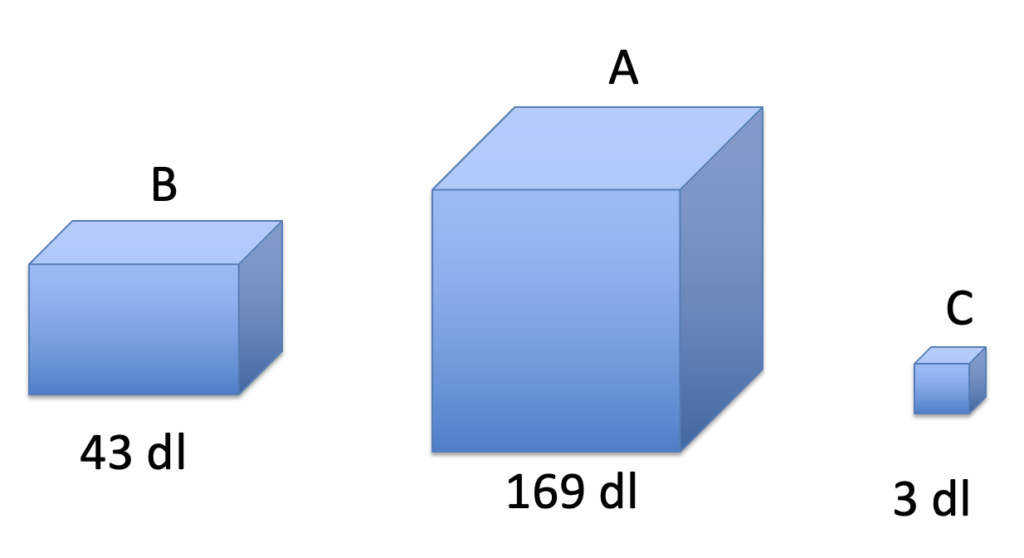
In questo caso si potrebbe anche riempire $C$ e svuotarne il contenuto in $A$ ripetendo questi due passaggi per $43$ volte. Ma nelle $43$ operazioni si perderebbero troppe gocce d’acqua che renderebbero meno precisa la quantità d’acqua contenuta alla fine nel contenitore $A$ (non è una strategia ottimale, ci sono troppe operazioni).
Subito di seguito, dopo aver commentato la soluzione precedente, si propone alla classe la stessa situazione con dati ancora diversi.
Hai a disposizione dei contenitori non graduati $A$, $B$ e $C$ che pieni contengono rispettivamente $49$ dl, $23$ dl e $3$ dl. Hai acqua a volontà per riempirli. Puoi riempire un contenitore, svuotarne il contenuto in un altro, svuotare il contenuto per terra: puoi fare quello che vuoi. Alla fine devi ottenere un contenitore che contenga $20$ dl.
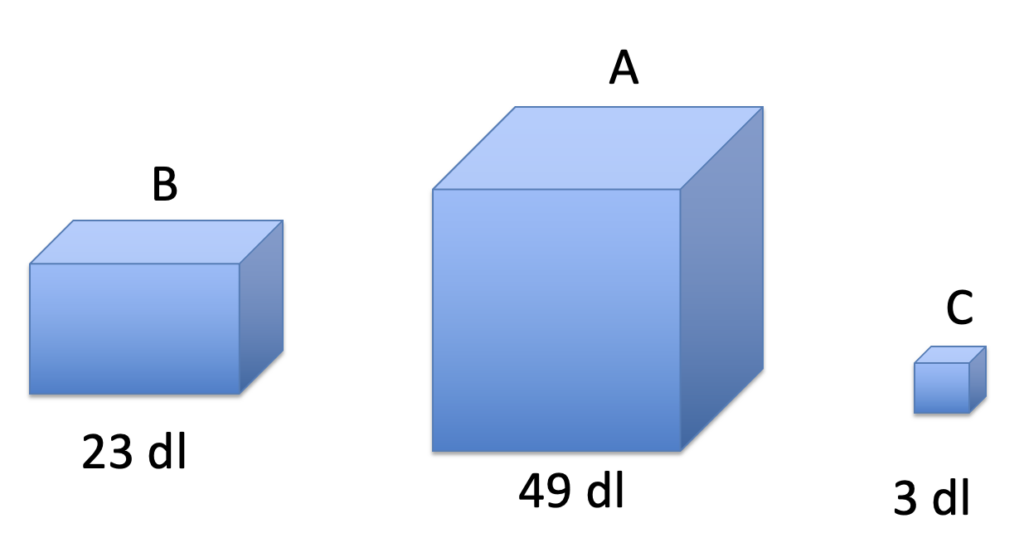
La soluzione $A-B-2C$ funziona ancora e tutti la provano subito; è però più efficace la soluzione $B-C$, ma pochissimi in genere la individuano e la propongono come soluzione.
Questo tipo di esercitazioni aiuta a far osservare a studentesse e studenti che è bene sempre cercare una soluzione personale che più si adatti alla situazione problematica anziché cercare di ricordare qualcosa di già svolto e applicarlo meccanicamente.
All’inizio dell’articolo ho parlato di alcuni opportuni indicatori di osservazione da utilizzare durante questo tipo di attività di problem-solving.
Qui di seguito alcuni esempi:
- tempo intercorso dalla lettura del testo al primo tentativo autonomo di risoluzione
- numero di soluzioni originali adottate
- quante volte studentesse e studenti ascoltano e cercano di capire strategie alternative proposte da altri
- quante volte studentesse e studenti verificano personalmente la procedura di risoluzione di un problema prima di sottoporlo ad altre persone
Offriamo dunque alle studentesse maggiori possibilità di conoscere le proprie personali capacità matematiche, con uno sguardo particolare che cerchi di cogliere lo sviluppo delle loro reazioni: magari cercando di far ciò scopriamo anche alcune nostre sconosciute capacità didattiche!
