
Voi insegnanti sapete bene come in matematica sia fondamentale la padronanza della gestione di più linguaggi, da quello verbale a quello simbolico o a quello grafico pittorico e come sia essenziale, di conseguenza, anche la flessibilità nel passaggio da uno di essi a un altro. La molteplicità dei linguaggi non solo favorisce una migliore comprensione delle situazioni problematiche che si possono incontrare, a scuola o nella vita, ma può suggerire strategie differenziate di soluzione, collegabili ad aree diverse di sapere, da utilizzare opportunamente o comunque da rivedere o sistemare in modo funzionale ai casi considerati.
Come già è avvenuto in mie precedenti proposte, anche l’attività didattica che vi descrivo qui riguarda proprio questo aspetto, perché il testo del problema è da interpretare adeguatamente, è suscettibile di strategie risolutive differenti e si presta a interessanti riflessioni sui linguaggi utilizzabili. Come vedrete, l’attività potrebbe essere adatta a una seconda o terza classe di secondaria di primo grado ma anche a una prima classe di secondaria di secondo grado, come occasione per rivedere e consolidare insieme, in situazione, alcune proprietà elementari delle operazioni con le potenze.
Lo svolgimento dell’attività risolutiva in collaborazione sarebbe, a mio parere, preferibile a un’attività individuale, soprattutto perché i possibili fraintendimenti potrebbero essere utilmente discussi tra gli alunni stessi, dando loro la possibilità di esprimersi liberamente su proprietà aritmetiche di base, come quelle legate alle proprietà delle potenze e sulla loro espressione simbolica.
Ecco il testo del problema:
Un vascello spaziale parte dalla Terra verso un pianeta situato a $2^{20}$ km. Dopo aver percorso un quarto del tragitto perde il contatto radio con la Terra. Quando il contatto viene ristabilito, il vascello si trova a $2^{19}$ km dalla Terra. Quanti km ha percorso il vascello spaziale senza contatto radio?
Si può notare che nella formulazione del testo si mescolano linguaggio verbale e notazioni simboliche delle potenze, che si intrecciano sia nella fase di interpretazione del contesto che in quella di ricerca del procedimento risolutivo.
Anzitutto è necessario comprendere che la dicitura “un quarto del tragitto” vuol dire dividere per $4$ i $2^{20}$ km totali da percorrere, ossia moltiplicarli per $\dfrac{1}{4}=\dfrac{1}{2^{2}}$.
Quindi i kilometri percorsi nel momento in cui il vascello spaziale perde il contatto radio risultano essere:
$2^{20}:4=2^{20}:2^{2}=2^{20-2}=2^{18}$
oppure, in modo equivalente:
$2^{20}\cdot \dfrac{1}{2^{2}}=\dfrac{2^{20}}{2^{2}}=2^{20-2}=2^{18}$
Il contatto viene ristabilito quando il vascello si trova a $2^{19}$ km dalla Terra, quindi il tratto percorso senza contatto radio è dato dai kilometri tra $2^{18}$ e $2^{19}$ e tale valore si può trovare ovviamente come differenza:
$2^{19}-2^{18}=2^{18}\cdot 2-2^{18}=2^{18}$ km
Si può anche procedere diversamente, osservando che $2^{19}=2^{18+1}=2^{18}\cdot 2$ e da ciò si conclude che il vascello, senza contatto radio, ha percorso esattamente lo stesso numero di kilometri del primo tratto, ossia $2^{18}$ km.
In un altro modo ancora, se si osserva che $2^{19}=2^{20-1}=2^{20}\cdot \dfrac{1}{2}$, risulta evidente che il vascello ristabilisce il contatto quando si trova esattamente a metà del tragitto totale. Quindi, ancora, senza contatto radio il vascello ha percorso un quarto del tragitto $( \dfrac{1}{2}-\dfrac{1}{4}= \dfrac{1}{4}) $, cioè $2^{18}$ km.
Senza dubbio potrebbe essere utile, nell’interpretazione della situazione e delle scritture simboliche adottate, appoggiarsi a una rappresentazione grafica, come la seguente:
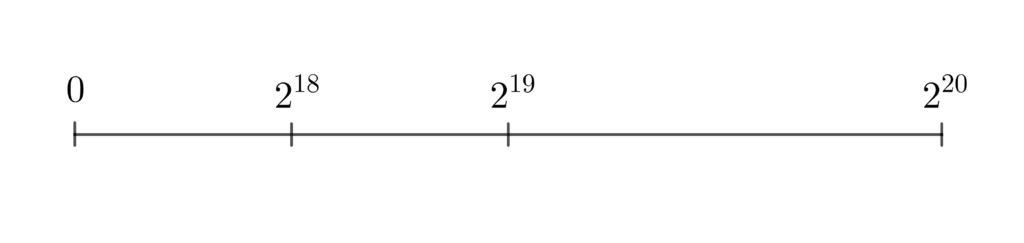
È evidente, tuttavia, che una rappresentazione grafica scorretta, in cui per esempio la collocazione di $2^{19}$ risulti molto vicina a $2^{20}$, potrebbe costituire un ostacolo decisamente fuorviante: sarebbe tuttavia occasione di discussione sulla notevole differenza tra una rappresentazione lineare e una esponenziale. Un opportuno collegamento, in questo senso, potrebbe essere anche il confronto tra i grafici delle funzioni $y=2n$ e $y=2^{n}$, proprio come previsto dalle Indicazioni Nazionali.
Un’ulteriore strategia di risoluzione, a cui gli alunni spesso ricorrono, potrebbe essere quella di utilizzare una calcolatrice per il calcolo delle potenze presenti nel problema, procedendo dunque così:
$2^{20}=1048576$
$\dfrac{1}{4}$ del tragitto $=262144=2^{18}$
$2^{19}=524288$
$2^{19}-2^{18}=262144=2^{18}$
È interessante osservare, a proposito di quest’ultima soluzione, che nelle esperienze in classe essa ha spesso destato molte perplessità: coloro che l’avevano proposta pensavano di avere sbagliato il calcolo perché non erano convinti del fatto che $2^{19}-2^{18}$ desse $262144$, lo stesso numero che avevano calcolato in corrispondenza di $2^{18}$.
Non accettavano dunque l’uguaglianza $2^{19}-2^{18}=2^{18}$, cioè, quindi, che $2^{18}$ è la metà di $2^{19}$.
Questa perplessità è sempre stata oggetto di discussioni molto articolate in cui si sono accostati calcolo, scritture con potenze, proprietà delle potenze e rappresentazioni grafiche opportune, con l’esigenza di concordare l’evidenza dei calcoli con le proprietà delle potenze note e le loro interpretazioni nel contesto assegnato.
Ciò che si può concludere, dunque, è che spesso le proprietà aritmetiche di base, come quelle legate alle potenze, sono recitate e anche applicate in modo meccanico, senza la dovuta padronanza dei significati che esse comportano. Un problema come quello presentato, semplice ma allo stesso tempo fonte di fraintendimenti ed errori su cui discutere, può dunque contribuire a potenziare la consapevolezza sul significato del simbolismo e delle procedure messe in gioco, a favore di una progressiva autonomia nel ricorso alle idee e agli strumenti della matematica.
