
Quando si propone un problema a studentesse e studenti, è bene sottolineare che spesso non esiste un solo modo per risolverlo, se è un vero problema. Proporre problemi con diverse strategie risolutive e impegnare tempo per confrontare queste strategie valutando un’eventuale ottimizzazione dei procedimenti risolutivi (meno calcoli, meno risorse – mentali, temporali – impiegate, meno probabilità di errore) costituisce un approccio che può essere funzionale a sviluppare competenze di problem solving, soprattutto quando le diverse strategie riguardano ambiti diversi (algebrico, grafico, geometrico) o meglio interessano ambiti diversi anche all’interno della stessa strategia. Potrebbe essere, inoltre, un modo bellissimo per far intuire a studentesse e studenti che tutto torna in matematica, come questa meravigliosa disciplina offra vari modi, anche molto diversi fra loro, per verificare la correttezza di una strategia risolutiva o per risolvere un dubbio su una formula.
Di seguito vi propongo un esempio che offre anche la possibilità di generalizzare la strategia risolutiva seguendo un approccio di modellizzazione matematica (matematizzazione della situazione reale, ricerca della relazione diretta tra dati iniziali e finali del problema) introducendo così in modo fattibile per le studentesse e gli studenti questo particolare, potente, strumento matematico.
È preferibile descrivere il problema sempre attraverso un approccio di storytelling che simuli una situazione reale. Questa tecnica, oltre a motivare la classe, aiuta anche a sviluppare la capacità di selezionare da un testo articolato le informazioni necessarie per rispondere a una determinata domanda posta.
La mamma di Silvia organizza la festa di compleanno per la figlia comprando varie cose da mangiare e la torta. Arrivata a casa inizia a predisporre il cibo, i tavoli, le sedie e si dimentica di mettere in frigo la torta come le era stato raccomandato. Cerca di rimediare mettendo la torta in freezer appoggiata su un vassoio, ma la lascia per troppo tempo. Quando è arrivato il momento di servirla si accorge che la parte superiore della torta e tutta quella laterale sono ghiacciate.
La torta è a forma di parallelepipedo ed era già stata divisa in porzioni corrispondenti a dei cubetti. Le porzioni che hanno anche solo una faccia ghiacciata non sono commestibili. Se la torta è larga $30$ cm, profonda $15$ cm e alta $9$ cm e lo spigolo delle porzioni è di $3$ cm, aiuti la mamma di Silvia a capire quante porzioni commestibili ha a disposizione per la festa?
Normalmente in ogni classe le studentesse e gli studenti (preferisco sempre farli lavorare in piccoli gruppi) utilizzano strategie diverse per calcolare quante porzioni rimangono commestibili. Di seguito alcuni esempi.
Primo tipo di strategia
Dei gruppi iniziano calcolando il volume della torta e quella della singola porzione e dal loro rapporto individuano il numero totale di porzioni. È interessante notare chi effettua il calcolo nel seguente modo:
Volume torta: $30\cdot 9\cdot 15=4050$ cm$^{3}$
Volume di ogni porzione: $3^{3}=27$cm$^{3}$
e chi direttamente considera il rapporto fra i due volumi semplificando i vari termini del numeratore con il denominatore:
n. porzioni totali: $\dfrac{30\cdot 15\cdot 9}{3^{3}}=150$
Questi gruppi calcolano poi le porzioni parzialmente congelate (non commestibili) e per sottrazione arrivano a definire quelle commestibili. Spesso nel calcolare quelle parzialmente congelate contano le porzioni che fanno parte di ogni singola faccia ghiacciata della torta finendo per considerare, nel calcolo, due, tre volte la stessa porzione che, appartenendo a due o più facce esterne, ha più di una parte congelata. Raramente deducono il numero corretto di porzioni non commestibili.
n. porzioni parzialmente congelate: $102$
n. porzioni commestibili: $150-102=48$
Secondo tipo di strategia
Altri gruppi dividono la torta a strati orizzontali e verticali (di altezza e larghezza, rispettivamente, pari alla dimensione della porzione) e cercano di capire in modo empirico, intuitivo, quasi senza effettuare operazioni, le porzioni corrispondenti agli strati completamente interni. Generalmente non arrivano mai a calcolare il numero corretto di porzioni commestibili.
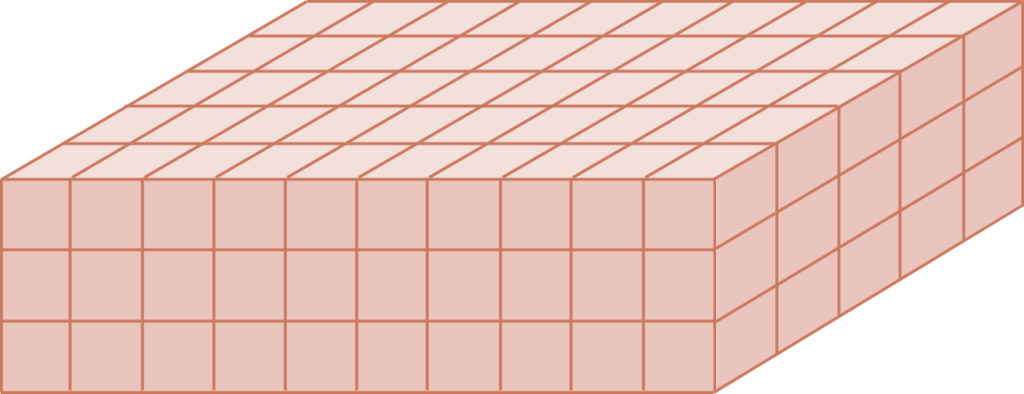
Terzo tipo di strategia
Altri gruppi considerano prima la torta a strati orizzontali, deducono che lo strato superiore non deve essere conteggiato nel computo delle porzioni commestibili, mentre per gli strati rimanenti intuiscono che le porzioni commestibili sono le stesse per ogni strato. Si limitano quindi a conteggiare le porzioni interne in uno strato che non abbiano alcuna faccia congelata.
n. di strati orizzontali (altezza della torta diviso dimensione spigolo porzione): $9:3=3$
n. di strati aventi porzioni commestibili (n. strati totali meno $1$, lo strato superiore): $3-1=2$
n. porzioni commestibili per ogni strato: $3\cdot 8=24$ (solo le porzioni totalmente interne)
n. porzioni totali commestibili (n. strati per numero porzioni commestibili per ogni strato): $2\cdot 24=48$
Confrontate le varie strategie utilizzate generalmente tutta la classe concorda che la terza strategia è la più semplice dal punto di vista del calcolo, offre meno probabilità di compiere errori e si dimostra essere anche la più rapida.
Nonostante questa strategia venga spiegata nel dettaglio a tutta la classe, spesso si verifica che se poi si ripropone lo stesso problema aumentando le misure della torta e delle porzioni, le studentesse e gli studenti si immergano nuovamente in molteplici calcoli. C’è chi ripercorre l’intero procedimento, chi ripete in sequenza le stesse operazioni con numeri differenti e chi cerca nuovamente strategie alternative, in modo empirico, impegnando molto tempo per poi dedurre un numero di porzioni commestibili errato.
Per esempio, in un secondo momento possiamo invitare a risolvere il problema della torta indicando alla classe le seguenti dimensioni:
$60$ cm, $30$ cm, $15$ cm per la torta
$5$ cm per lo spigolo della porzione
Si può registrare il tempo che studentesse e studenti impiegano a trovare il numero di porzioni commestibili in questo secondo caso, facendo loro osservare come, nonostante l’avessero già risolto, cambiando i dati non sia comunque rapido ripercorrere tutta la strategia risolutiva applicata nel caso precedente, per quanto simile.
Dalla mia esperienza, ho notato che per far capire l’importanza e l’efficacia dei modelli matematici è bene che studentesse e studenti sperimentino questo strumento dopo aver individuato autonomamente strategie risolutive alternative.
Dopo aver provato nuovamente a risolvere il problema con dimensioni diverse possiamo mostrare a studentesse e studenti come modellizzare la situazione: associamo alle caratteristiche della torta delle variabili matematiche indicando con $l$, $p$, $h$ e $d$ rispettivamente larghezza, profondità, altezza della torta e dimensione della porzione di torta.
Indichiamo inoltre con $n$ il numero delle porzioni commestibili.
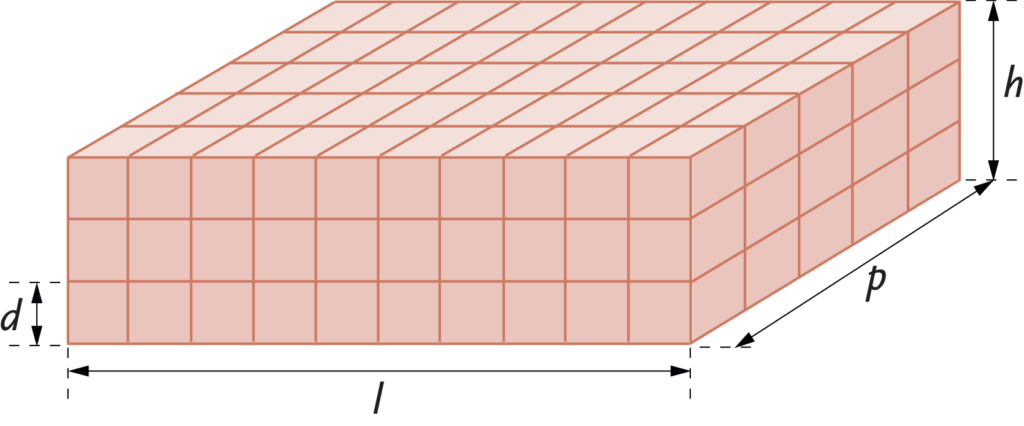
Cerchiamo con la classe di individuare una relazione diretta fra le porzioni commestibili totali e queste variabili.
n. strati orizzontali con porzioni commestibili: $h:d-1$
n. porzioni commestibili per ogni strato orizzontale: $\left( l:d- 2\right) \left( p:d-2\right)$
porzioni commestibili totali: n. strati $\times$ numero porzioni commestibili per ogni strato
porzioni commestibili: $n=\left( h:d-1\right) \left( l:d-2\right) \left( p:d-2\right)$
Qualsiasi siano le dimensioni della torta e delle porzioni, il calcolo delle porzioni commestibili è così immediato.
Inoltre, la relazione permette anche di decidere, date le dimensioni della torta e il numero di porzioni commestibili necessarie, quanto deve essere la dimensione delle porzioni.
Quello proposto è solo un semplice esempio di come la stessa situazione problematica possa essere ampiamente sfruttata, spero sia stata da stimolo per tante altre idee valide e interessanti da condividere fra colleghi.
