
L’attività che vi propongo riguarda un problema geometrico molto classico ed è collegato ad esperienze didattiche che sono state svolte più volte con insegnanti di scuola secondaria nell’ottica di continuare a sviluppare un insegnamento per problemi che promuova negli alunni alcune importanti competenze: saper ricorrere alle conoscenze più adeguate alla situazione che si sta affrontando, saper scegliere strategie, saper prendere opportune decisioni e riuscire poi a controllare gli esiti ottenuti, con ulteriori eventuali riflessioni più generali.
L’attività dovrebbe essere svolta preferibilmente a gruppi, soprattutto se si discosta abbastanza dalle situazioni problematiche cui i vostri alunni sono abituati, perché in questo caso è preferibile che siano disponibili più risorse cognitive, come appunto accade se si lavora insieme e si affronta in collaborazione la novità del compito. Se invece siete già abituati a proporre in classe situazioni piuttosto aperte, che richiedono l’iniziativa dei vostri studenti, l’attività potrebbe essere anche svolta individualmente, senza il pericolo che si scoraggino o si blocchino. In entrambi i casi sarà comunque cruciale il momento del confronto e della discussione degli esiti, che voi insegnanti saprete coordinare e sintetizzare in base agli interventi di tutti, arrivando così a una versione condivisa delle proposte e delle considerazioni emerse.
Ecco il testo del compito:
Utilizzando solo riga non graduata e compasso costruite due triangoli isosceli con procedimenti differenti e completate le figure ottenute descrivendo i passi e le motivazioni delle costruzioni eseguite.
La richiesta di produrre due triangoli isosceli con procedimenti grafici diversi vuole sollecitare l’inventiva degli alunni, per evitare che si riducano eventualmente a proporre la sola costruzione grafica già nota, perché vista in attività didattiche precedenti, durante l’ora di Matematica o di Tecnologia. L’attività prevede dunque che le uniche operazioni di costruzione siano quelle realizzabili con riga non graduata e compasso, cioè il tracciamento di rette, semirette o segmenti (senza misurazioni) e il tracciamento di circonferenze1: questo potrebbe essere già noto agli alunni e dunque essere richiamato prima di dare avvio al lavoro, oppure potrebbe essere un momento di riflessione collettivo, così da comprendere bene e condividere insieme queste regole del gioco.
Il compito proposto potrebbe sembrare troppo libero, perché non fa riferimento ad alcun calcolo o formula e inoltre richiede di verbalizzare i passi che si scelgono per le costruzioni: questo potrebbe essere un ostacolo se la classe non è abituata ad argomentare costruzioni grafiche, tuttavia questa fase è importante perché favorisce la riflessione sulla scelta delle proprietà che caratterizzano un triangolo isoscele e da tradurre in opportune costruzioni, sviluppando la consapevolezza di come gli strumenti considerati possano essere collegati alle proprietà geometriche scelte.
Poiché il triangolo isoscele è una figura familiare fin dalla scuola primaria, il problema può essere proposto a partire dalla conclusione della scuola primaria fino alle prime classi della scuola secondaria di secondo grado: ovviamente con la richiesta, per ogni costruzione proposta, di argomentazioni geometriche, più consapevoli e mature per gli alunni più grandi.
La possibilità di utilizzare carta quadrettata può ovviamente facilitare il compito e dunque potrete optare per questa scelta oppure richiedere costruzioni su fogli non quadrettati a seconda del livello della classe o lasciando agli alunni stessi la possibilità di scegliere la modalità che preferiscono: in quest’ultimo caso risulterà poi interessante confrontare e far emergere vantaggi e svantaggi di costruzioni fatte su carta quadrettata oppure no.
Le strategie possibili per costruire un triangolo isoscele con tali strumenti sono numerose e ovviamente ne potreste reperire altre in rete, anche per iniziativa degli alunni. Qui vi presento le più semplici, con osservazioni che potrete ampliare come riterrete più adeguato per la vostra classe.
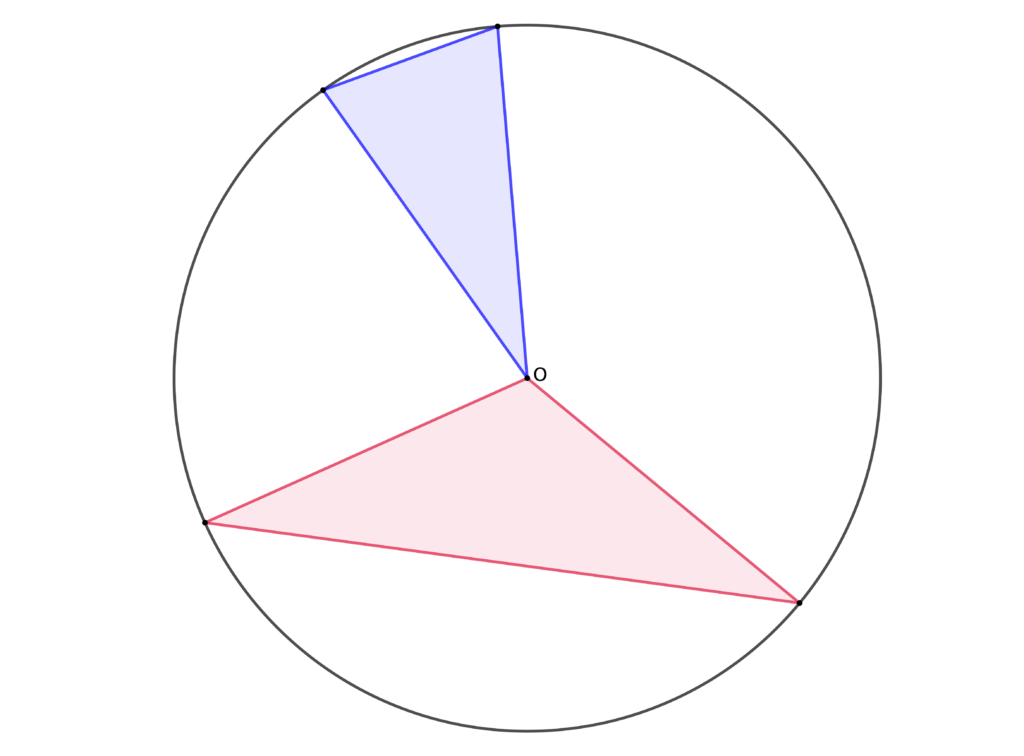
Una prima costruzione, molto semplice, potrebbe essere collegata alla proprietà di ogni triangolo isoscele di avere due lati fra loro congruenti e alla riflessione su ciò che produce un compasso: una circonferenza, che individua infiniti segmenti congruenti fra loro, cioè i raggi. Ecco allora che tracciata col compasso una generica circonferenza, è sufficiente unire il centro $O$ della circonferenza con due qualsiasi altri punti della stessa per ottenere i lati di un triangolo isoscele, che proprio perché sono raggi della medesima circonferenza hanno uguale misura. La figura si completa ovviamente unendo i due punti individuati sulla circonferenza. Ecco due esempi di triangoli isosceli così costruiti:
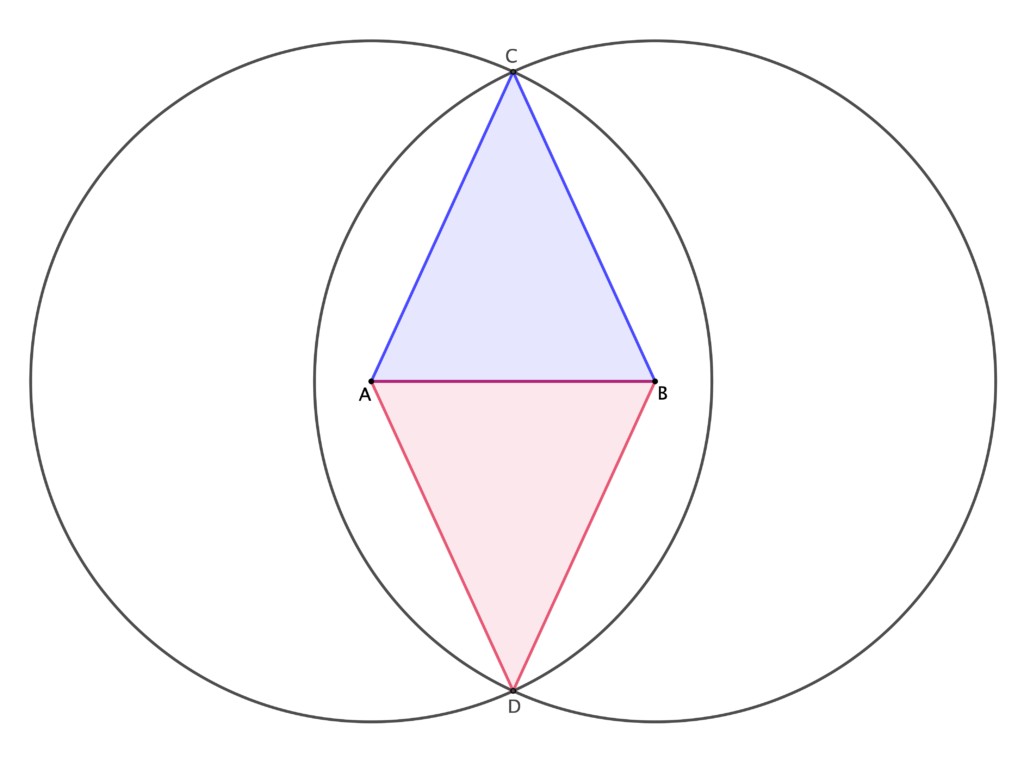
Una seconda costruzione, più usuale, potrebbe essere proposta dagli alunni che ricordano eventualmente quella già vista con l’insegnante di Tecnologia, a partire da un segmento come base del triangolo isoscele che si vuole costruire. Tracciato quindi un segmento qualsiasi $AB$ con l’utilizzo della riga, si disegna una circonferenza centrata in $A$ con apertura del compasso opportuna2 (…si può scoprire in seguito, in sede di discussione e giustificazione di questo passaggio costruttivo, cosa significhi apertura del compasso opportuna, arrivando a dire che l’apertura del compasso deve essere superiore alla metà del segmento $AB$, altrimenti le due circonferenze non si intersecano e i punti $C$ e $D$ non si formano!). Si ripete la medesima operazione centrando in $B$. Ciascuno dei due punti di intersezione delle due circonferenze rappresenta il vertice di un triangolo isoscele. Se ne completa uno per esempio nel modo seguente (e si nota che in effetti se ne ottengono due, simmetrici rispetto ad $AB$).
Una terza costruzione, che potrebbe emergere dai ragazzi oppure offerta loro da voi insegnanti attraverso il solo disegno da interpretare, si ricava a partire dall’individuazione dell’asse di simmetria, procedendo come nella seconda costruzione. Ecco dunque la figura che potreste proporre, nel caso che non emerga già nella vostra classe, da interpretare in funzione del compito assegnato:
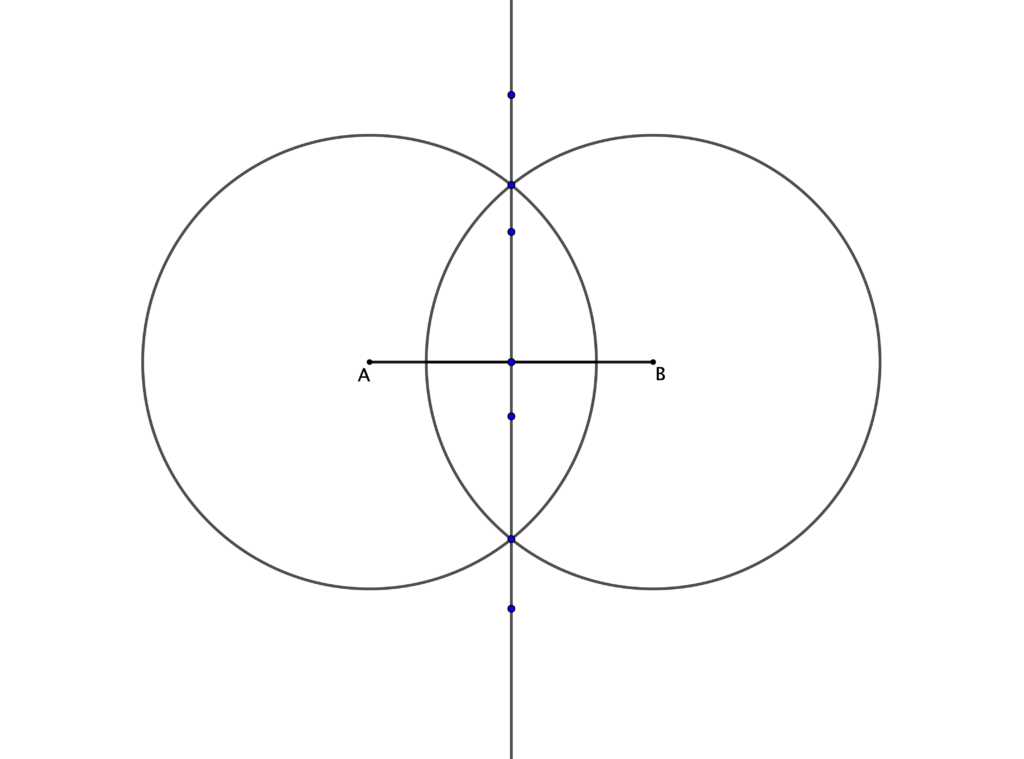
È evidente che, costruito l’asse di simmetria del segmento $AB$, la figura dovrebbe suggerire che qualsiasi punto dell’asse, unito ad $A$ e $B$, genera un triangolo isoscele: la proprietà cui si fa ricorso è quella dell’asse di simmetria di un segmento come luogo dei punti del piano equidistanti dagli estremi del segmento, cioè l’asse è l’insieme di tutti e soli i punti del piano con questa proprietà. Si tratta di qualcosa che risulta familiare fin dalla scuola primaria e che nella scuola secondaria può essere ripreso ed argomentato in più occasioni, a partire dall’evidenza concreta offerta da attività sulle piegature, che già mette in evidenza che segmenti simmetrici sono congruenti, fino ad argomentazioni più mature e comunque coerenti con l’impostazione geometrica condivisa con la classe (per esempio, se si caratterizza l’asse di simmetria di un segmento come perpendicolare nel suo punto medio, la congruenza dei due lati obliqui sarà conseguenza della congruenza dei due triangoli rettangoli che hanno i lati obliqui come ipotenusa).
Da questa costruzione si ricava dunque facilmente che ogni punto dell’asse di simmetria può essere definito come vertice $C$ del triangolo isoscele $ABC$, di lati obliqui congruenti $CA$ e $CB$ e dunque la strategia permette di ottenere infiniti triangoli isosceli.
In conclusione, l’attività proposta risulta molto aperta, suscettibile quindi di potersi adeguare facilmente alla situazione cognitiva dei vostri alunni, con opportuni ampliamenti o riduzioni a seconda della loro reazione al compito. La scelta delle strategie costruttive e soprattutto le motivazioni collegate ai procedimenti scelti (che è sempre bene far tradurre in verbalizzazioni scritte da condividere e su cui riflettere) fanno emergere ciò che gli studenti riescono a mettere in gioco non solo sulle loro conoscenze geometriche di base ma anche sulle modalità argomentative e sulle capacità decisionali che hanno maturato, offrendo a voi insegnanti la possibilità di valutare il grado di sviluppo di tali loro competenze, anche al fine di progettare al meglio i momenti didattici successivi.
1 Come è noto, il problema di quali costruzioni geometriche siano possibili con riga non graduata e compasso è classico e qualora non sia ancora stato affrontato potrebbe essere questa un’occasione per avviarlo, soprattutto a conclusione della scuola secondaria di primo grado o meglio alla scuola secondaria di secondo grado. La situazione potrebbe essere anche collegata all’utilizzo di un software geometrico come GeoGebra, tuttavia qui ho scelto di riferirmi agli strumenti concreti, di cui mi sembra utile che gli alunni abbiano comunque un’esperienza diretta.
2 A proposito di apertura del compasso è utile ricordare che i classici problemi di costruzioni con riga e compasso, collegati analiticamente alla risolubilità di un’equazione di secondo grado, prevedono, oltre alla riga non graduata, un compasso “molle”, cioè che non possa conservare l’apertura. Tuttavia si può dimostrare che con l’utilizzo della riga non graduata e di un compasso “molle” si può simulare l’utilizzo di un compasso rigido, cioè che mantenga l’apertura e dunque è comunque possibile, come si è soliti fare pensando alle caratteristiche di un usuale compasso, fare riferimento al compasso rigido, come nella costruzione proposta.
