
Aria di vacanze e voglia di partire. Allora costruiamoci una barca di carta e… mettiamola in coordinate!
La barca può essere piegata dai vostri studenti e poi voi potrete lasciare un “compito” per le vacanze.
Ecco le istruzioni. Si parte da un triangolo rettangolo isoscele, bianco da un lato e colorato dall’altro, oppure di due colori diversi sulle due facce, come nell’esempio in figura. Se avete carta origami quadrata in classe, basterà tagliare i fogli lungo la diagonale. Altrimenti potete usare fogli bianchi che i ragazzi personalizzeranno una volta piegato il modello.
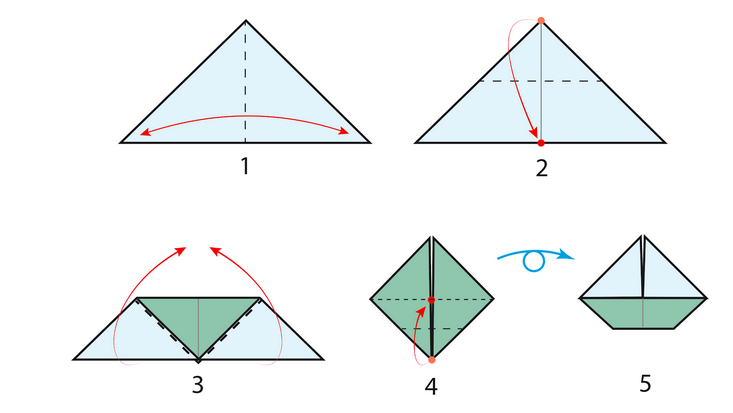
- Partiamo da un triangolo rettangolo isoscele. Pieghiamo l’altezza relativa all’ipotenusa e riapriamo.
- Portiamo ora il vertice dell’angolo retto sul piede dell’altezza. Notiamo che la figura resta divisa in tre triangoli congruenti: due azzurri e uno verde.
- Pieghiamo lungo le linee di cambio colore, portando i triangoli azzurri verso l’alto. Apparirà un quadrato verde.
- Pieghiamo il vertice in basso del quadrato (dove ci sono più strati di carta) fino al centro del quadrato stesso.
- Voltiamo la frittata: ecco la barca a vela.
Incolliamo la barca su un foglio, meglio se bianco. Potrebbe essere utile avere anche un’altra barchetta da riaprire per considerazioni geometriche.
Attività 1. Inizialmente, insieme agli studenti fissate un sistema di riferimento (origine, asse x e asse y) e un’unità di misura. La foto illustra la mia scelta degli assi e la notazione dei punti; per l’unità di misura ho posto 1 la distanza del punto A dall’origine.
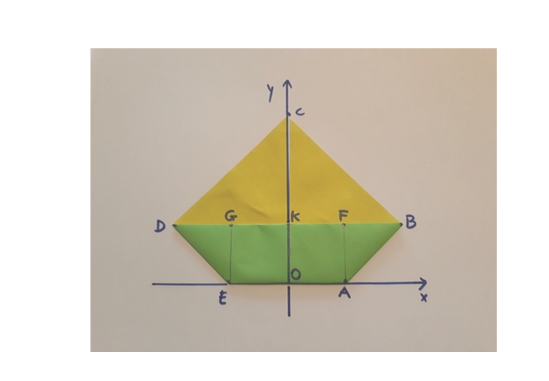
Ecco una serie di domande tra le quali potete scegliere per l’esercizio delle vacanze, aggiungendone poi altre a vostro piacere.
i) Posto A(1,0), calcolare le coordinate dei punti B, C, D, E, F, G, K.
Invitate i ragazzi a utilizzare le simmetrie della figura per velocizzare l’esercizio.
Suggerimento: per calcolare le coordinate di B, osservate che OA ≅ FA (lo si può controllare sovrapponendo i lati oppure con semplici considerazioni, anche riaprendo parzialmente un modello identico che non avete incollato) e FB ≅ FA (lo si può controllare sia sovrapponendo i due segmenti sia mostrando che il triangolo ABF è metà quadrato).
ii) Calcolare (anche in più modi) l’area dello scafo e l’area delle vele.
Questo punto è interessante perché può essere risolto usando le coordinate o, più velocemente, con osservazioni di geometria sintetica.
Per esempio, il trapezio dello scafo si può scomporre in 2 quadratini di area 1 più due triangolini, ognuno dei quali vale metà quadrato. Quindi l’area è 3.
L’osservazione è importante perché a volte, dopo aver introdotto le coordinate, gli studenti tendono a “opporsi” a ragionamenti sintetici. Ovviamente si può utilizzare anche la formula dell’area del trapezio.
Le vele formano un quadrato di lato KB, ed è quindi immediato il calcolo della loro area.
Per il perimetro bisognerà sapere che in un quadrato si ha
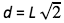
se d è la diagonale ed L è il lato del quadrato.
iii) Calcolare le equazioni di alcune rette formate dalle pieghe della barca.
Per esempio, potete chiedere le equazioni delle rette per le seguenti coppie di punti: D e B, A e B, D ed E, O e C.
Si può chiedere ai ragazzi anche di fare alcune riflessioni sui coefficienti delle equazioni di coppie di rette simmetriche rispetto all’asse delle ordinate.
iv) Verificare la posizione reciproca di alcune coppie di rette (parallelismo e perpendicolarità).
v) Calcolare i punti di intersezione di alcune coppie di rette (per esempio le due rette su cui poggiano i lati obliqui dello scafo) o verificare che alcuni punti appartengano o no a una data retta.
Attività 2. Potete chiedere agli studenti di rifare l’esercizio con una barca identica ma con una scelta diversa del sistema di riferimento e/o dell’unità di misura. Per esempio, la foto che segue illustra una possibilità.
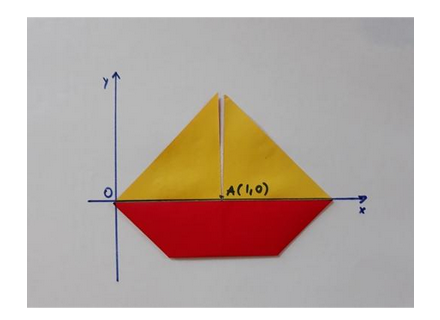
Attività 3. Potete suggerire agli studenti di piegare un modello a loro scelta e ripetere l’esercizio, introducendolo in un sistema di riferimento e calcolando coordinate di punti, rette, perimetri e aree.
