
Siamo tutti chiusi nelle nostre case, costretti a improvvisare una didattica a distanza che non conosciamo e che non abbiamo mai sperimentato e, tra mille dubbi e perplessità, ci domandiamo se sia meglio registrare le lezioni e invitare gli studenti a guardarle, fare lezione in streaming, assegnare esercizi guidati o mandare link a videolezioni già presenti in rete.
Tutte queste alternative presentano vantaggi e svantaggi, ma quello che è certo è che, qualunque scelta si faccia, una lezione di matematica a distanza è persino meno coinvolgente di una fatta in classe!
E allora, perché non approfittare di questa situazione per sperimentare forme veramente alternative di didattica, per esempio proponendo, invece di una lezione, un gioco didattico per ripassare le coordinate nel piano cartesiano, i concetti di parallelismo e perpendicolarità e molto altro?
Per iniziare a giocare inviate ai vostri studenti il tabellone che trovate in allegato e l’immagine della barchetta qui sotto (quest’ultima vi servirà per condividere con loro la nomenclatura).
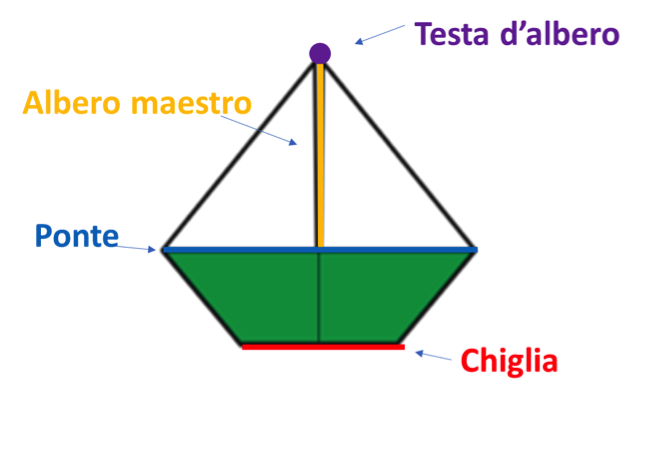
A questo punto, utilizzando un qualsiasi strumento per didattica a distanza che abbia una chat, comunicate a tutta la classe uno degli “ordini del capitano” che trovate nel file allegato. Ogni ordine contiene una lista di istruzioni che identificano la posizione di una (e una sola) delle barche le cui sagome sono presenti sul tabellone. Per vostra comodità (e per rapidità di correzione!), di fianco a ogni ordine ho inserito il numero della barca che gli corrisponde.
Il primo degli studenti che riesce a decodificare le informazioni e a identificare la barca corrispondente scrive sulla chat il numero della barca. Se la barca scelta corrisponde all’ordine dato, lo studente vince un punto, mentre se la barca scelta è errata, allo studente viene assegnato un punto di penalità.
Il gioco termina quando gli ordini sono esauriti. Il punteggio si calcola sommando il numero di ordini eseguiti correttamente e sottraendo le eventuali penalità dovute a ordini errati. Vince lo studente che totalizza il punteggio maggiore.
Potete anche proporre una modalità di gioco a squadre (due o tre studenti per squadra), suggerendo agli studenti di telefonarsi o di creare dei mini gruppi WhatsApp per discutere i diversi ordini in tempo reale.
Il gioco, che naturalmente potete ripetere e variare, sia inventando nuovi ordini che disegnando nuovi tabelloni, aiuterà gli studenti a imparare a muoversi con disinvoltura nel piano cartesiano, rafforzando gli automatismi sul riconoscimento di rette parallele e perpendicolari agli assi cartesiani.
Inoltre gli studenti impareranno a leggere con attenzione una consegna e a tradurre correttamente gli ordini ricevuti.
Per esempio, per comprendere il significato dell’ordine: «ll prodotto delle ordinate degli estremi del ponte è negativo» gli studenti dovranno tradurlo in «le ordinate degli estremi del ponte hanno segno opposto tra loro» ovvero «il ponte interseca l’asse delle ascisse».
Analogamente, per identificare la barca che corrisponde all’ordine: «Il prodotto dell’ordinata di tutti i punti della chiglia con l’ordinata della testa d’albero vale zero» è necessario ricordare la regola di annullamento del prodotto, traducendo quindi l’ordine precedente nell’informazione «o la testa d’albero ha ordinata nulla, oppure la chiglia sta sull’asse delle ascisse».
Sarà di grande soddisfazione vedere come, dopo un po’ di ordini decodificati con fatica, diventerà facile per i ragazzi capire che, quando il capitano dice: «L’ordinata della testa d’albero è minore dell’ordinata di tutti i punti della chiglia», la barca che stanno cercando sarà certamente tra quelle a testa in giù!
