
Si ricomincia. Ci eravamo lasciati l’anno scorso con un accenno al fatto che la matematica è un ponte tra fantasia e realtà e quest’anno forse vale la pena di approfondire un po’ la questione.
Prendiamo i numeri, per esempio.
Conosciamo i numeri naturali: 0, 1, 2, 3, 4 e così via.
A che cosa servono? Di sicuro a contare gli oggetti che abbiamo intorno: diciamo che su un albero ci sono 153 mele, o che per fare la bagna cauda per 15 persone servono 15 spicchi d’aglio.
Qui la matematica è realtà: serve per fare qualcosa. Poi se uno la applica alla lettera nel cucinare la bagna cauda potrebbe avere difficoltà a intrattenere relazioni con altre persone, ma non è certo questo il motivo principale per cui i matematici talvolta faticano a instaurare rapporti sociali.
Passiamo ai numeri interi: …, –5, –4, –3, –2, –1, 0, 1, 2, 3 e così via.
Leggiamo ad alta voce i numeri della sequenza e fermiamoci allo 0. Non è un conto alla rovescia? Se pronunciamo un numero ogni secondo, il nostro elenco può significare “mancano 5 secondi”, “mancano 4 secondi”, “mancano 3 secondi”, … Allo stesso modo, se ci dicono che il conto in banca è a –1000 euro, significa che siamo nei guai, perché mancano 1000 euro. Così, mentre i numeri positivi ci dicono quello che c’è, i numeri negativi ci dicono quello che manca. Lo zero ci dice che non c’è nulla.
Siamo di nuovo alla realtà: i numeri interi servono pure loro a qualcosa.
Ecco, se adesso provassimo ad addentrarci in qualche passaggio per vedere come, matematicamente, si passa dai numeri naturali alla costruzione dei numeri interi (perché i matematici l’hanno fatto eh – mica possiamo definire i numeri interi dicendo che servono per contare quello che c’è e quello che manca), allora sembrerebbe pura fantasia e probabilmente avremmo un’idea del perché talvolta i matematici faticano a instaurare rapporti interpersonali.
Ma non è finita: ci sono i numeri razionali. Detto così uno potrebbe pensare che questi numeri, così razionali, siano tipi un po’ noiosi, che non sgarrano mai. Invece il termine “razionale” viene dal latino (uh ecco, il latino, a proposito, sembra essere una di quelle altre cose che non servono a niente, come la matematica): in latino la parola “ratio” significa “rapporto”. Quindi i numeri razionali sono quelli che si scrivono come rapporti, cioè, per farla breve, le frazioni.
E sarebbe un guaio non averli, perché sarebbe impossibile, per esempio, dire “mi sono mangiato mezza tavoletta di cioccolato”.
Ma ci sono anche motivi più nobili: immaginiamo di misurare la lunghezza di un tavolo. A spanne potrebbe essere, per esempio, 16 e mezza: numero razionale. Poi, prendendo il metro, potremmo scoprire che il tavolo è lungo 3,16 m: altro numero razionale.
I numeri razionali, per dirne una, ci servono a esprimere le misure.
Certo che su un tavolo lungo 3,16 m si potrebbe comodamente mangiare la bagna cauda in 15…
Anche in questo caso i matematici hanno lavorato di fantasia per dare un senso, appunto, “matematico” ai numeri razionali.
Se poi consideriamo (una delle attività che piacciono di più ai matematici è “considerare”) un quadrato di lato lungo 1 m, quanto è lunga la sua diagonale? Per il teorema di Pitagora possiamo dire che è lunga
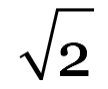
Adesso supponiamo di prendere un metro da sarto e vediamo un po’ se riusciamo a tirare fuori questo numero. Se c’è una tacca ogni millimetro, il massimo che potremo dire è che la diagonale è lunga 1,414 m. Ora: 1,414 è un numero razionale, mentre si dice che
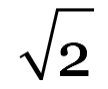
è un numero irrazionale.
A cosa servono i numeri irrazionali? Difficile dirlo, sembrano numeri completamente inaffidabili: hanno infinite cifre dopo la virgola e per di più piazzate a casaccio.
Si potrebbe andare avanti ancora, perché i razionali e gli irrazionali, presi insieme, formano i numeri reali: questa volta il nome ci dà una sensazione di sicurezza, andiamo tranquilli.
Ma poi ci sono gli immaginari (mamma mia…) e i complessi (già il nome è tutto un programma).
Pura fantasia? Macché: i numeri complessi servono a descrivere i circuiti elettrici e sono utili nella meccanica quantistica. È realtà.
Dunque dove sta la matematica tra realtà e fantasia? Sta a cavallo. A volte la matematica nasce da una necessità per poi prendere il volo nella fantasia. Ma molte altre volte accade che il frutto della fantasia sia utile per risolvere una nuova necessità, e così via. Quindi la matematica serve ed è bella: è un’invenzione continua che il più delle volte trova applicazione in un nuovo problema.
L’importante è andarci piano con l’aglio, che farà pure bene, ma ostacola molto le relazioni umane: la matematica invece non dovrebbe nuocere, se solo i matematici non andassero in giro a raccontare che cosa fanno…
Buon anno scolastico!
