
In questo articolo e nel successivo mi soffermerò su una particolare schematizzazione grafica, il grafo ad albero, che dalla scuola primaria alla scuola secondaria di secondo grado si può collocare molto utilmente in ambito probabilistico, anche se ovviamente può essere efficace in altri contesti, per esempio in aritmetica per visualizzare la scomposizione di un numero naturale in fattori primi o per rappresentare situazioni come quella della prima attività che vi descrivo di seguito.
Dunque, il grafo ad albero si aggiunge alle schematizzazioni (cioè tabelle, schemi a frecce e grafici cartesiani) che ho già commentato nei miei due precedenti articoli (Disegni, simboli, parole: collegare e interpretare rappresentazioni differenti e Dal linguaggio verbale di un problema alle differenti rappresentazioni dei suoi dati), con l’obiettivo generale di incrementare la vostra attenzione di insegnanti ma anche quella dei vostri alunni sulla consapevolezza di quanto un codice non verbale come quello grafico possa essere centrale nella conquista del pensiero matematico.
Ecco una semplice situazione che potete presentare ai vostri alunni per avviarli all’interpretazione di un grafo ad albero o per richiamarne il significato oppure per esplorare, dal vostro punto di vista, la consapevolezza degli studenti nell’utilizzo di questo tipo di schema.
Alla ricerca di strategie
In una scuola secondaria di primo grado i $\dfrac{12}{25}$ dei ragazzi frequentano le prime, $\dfrac{1}{3}$ le seconde e $70$ ragazzi le terze. La situazione può essere rappresentata così:
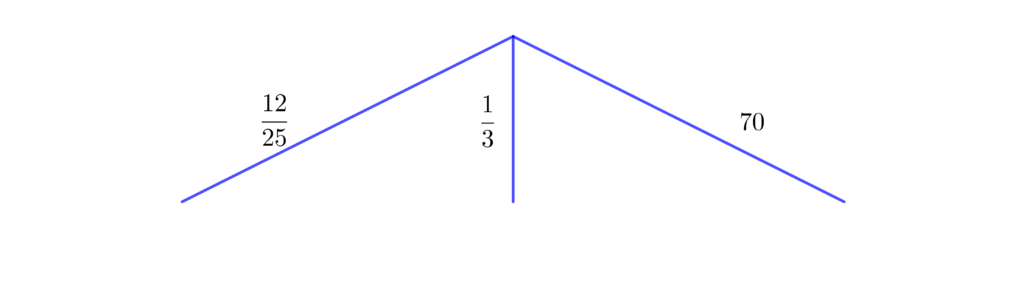
Quanti alunni frequentano le prime? Quanti le seconde?
Il grafo ad albero proposto non è certo indispensabile per rispondere ai due quesiti del problema, tuttavia è evidente che questa rappresentazione, da interpretare, descrive efficacemente il contesto proposto: ogni ramo rappresenta la numerosità di una classe e i dati lungo i rami sono dettati dal testo. È anche evidente che i dati sono espressi in modo diverso: i primi due sono impliciti, perché si riferiscono a numerosità non ancora note; il terzo dato, $70$, è esplicito e si riferisce alla numerosità dei ragazzi di terza.
Il problema, proposto in collaborazione a gruppi di alunni, in presenza ma anche a distanza, potrebbe essere particolarmente efficace per promuovere strategie risolutive differenti, oltre che per sollecitare discussioni sull’adeguata interpretazione dello schema proposto.
Le soluzioni potrebbero essere le seguenti: la prima non ricorre a un’equazione, dunque è adatta anche a inizio della scuola secondaria di primo grado; la seconda vi ricorre in parte e la terza utilizza (in modi diversi) un’equazione.
Prima soluzione. Riconosciuto che $1-\left( \dfrac{12}{25}+\dfrac{1}{3}\right) =\dfrac{14}{75}$ corrisponde a $70$ ragazzi, si ottiene subito che il numero totale dei ragazzi è $70\cdot \dfrac{75}{14}=375$, dunque il numero dei ragazzi che frequentano la seconda è $\dfrac{1}{3}\cdot 375=125$ e i ragazzi delle prime sono $375-70-125=180$, o in modo equivalente $\dfrac{12}{25}\cdot375=180$.
Seconda soluzione. Ricorrendo invece a una scrittura più compatta in equazione e indicando con $x$ il numero totale dei ragazzi della scuola, si ottiene (pensando al totale dei ragazzi come somma dei ragazzi di prima, seconda e terza), l’equazione:
$\dfrac{12}{25}x+\dfrac{1}{3}x+70=x$
oppure l’equazione equivalente (pensando che i $70$ ragazzi di terza sono dati dal totale meno i ragazzi di prima e seconda):
$x-\dfrac{12}{25}x-\dfrac{1}{3}x=70$
Si ottiene $x=375$, da cui poi si ricavano le numerosità richieste, come nel caso precedente.
Terza soluzione. Con una strategia intermedia rispetto alle due proposte, osservato che $1-\left( \dfrac{12}{25}+\dfrac{1}{3}\right) =\dfrac{14}{75}$ corrisponde a $70$ ragazzi e indicato con $x$ il numero totale degli alunni, si può scrivere $\dfrac{14}{75}x=70$ e trovare così $x=375$.
Il contesto della probabilità è forse il più interessante, a mio parere, per un utilizzo significativo di grafi ad albero, perché potrebbe consentire il trattamento di eventi casuali composti senza che siano proposti agli alunni né il concetto di eventi indipendenti né quello di probabilità condizionata1, anche se le probabilità condizionate sono tacitamente utilizzate lungo i rami del grafo, ovviamente in modo opportuno ma del tutto intuitivo. Le situazioni problematiche in questo contesto sono spesso assimilabili a estrazioni successive da un’urna, con o senza reimbussolamento: costruito un grafo ad albero adeguato si è di solito nella possibilità di associare le probabilità (condizionate) ai vari rami e la regola di moltiplicare lungo i rami scaturisce spontaneamente dal concetto di frazione di frazione. Vediamo un esempio di attività di questo tipo, che chiarisce quanto ho descritto e potrebbe essere affrontata in collaborazione, condividendo il significato e l’efficacia del simbolismo proposto.
Estrazioni da un sacchetto di palline
In un sacchetto ci sono $12$ palline: $2$ bianche, $3$ rosse e $7$ nere.
Se estraggo a caso una pallina:
a) Qual è la probabilità che sia nera?
b) Qual è la probabilità che sia bianca o rossa?
Se estraggo due palline, senza reimmettere la prima estratta nel sacchetto:
c) Qual è la probabilità che siano entrambe nere?
In questo caso gli eventi possibili, alla prima estrazione, sono tre: estraggo una pallina bianca ($B$), oppure rossa ($R$), oppure nera ($N$). La prima parte del grafo potrebbe essere questa, dove alla fine di ogni ramo è utile denotare l’evento rappresentato ($B$, $R$ o $N$) e su ogni ramo scrivere la probabilità che si verifichi quell’evento.
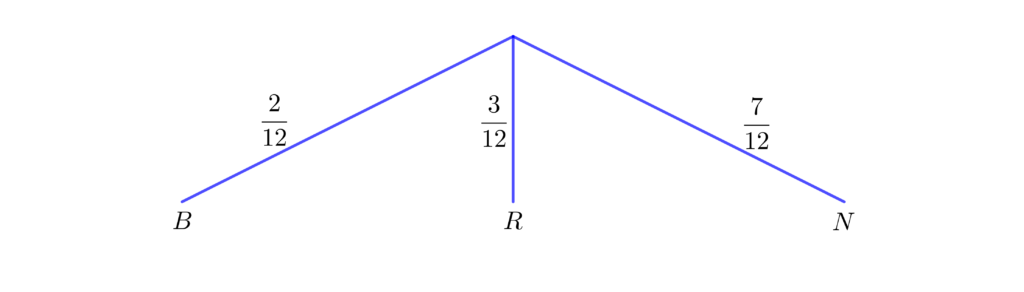
È evidente che la probabilità di estrarre una pallina nera è $p\left( N\right) =\dfrac{7}{12}$; la probabilità di estrarre una pallina bianca o rossa, cioè $p\left( B\cup R\right) $, si può vedere sia come $p\left( B\right) +p\left( R\right)$, cioè $p\left( B\cup R\right) =\dfrac{2}{12}+\dfrac{3}{12}=\dfrac{5}{12}$, oppure come l’evento “complementare” di $N$ con probabilità, dunque, $1-\dfrac{7}{12}=\dfrac{5}{12}$.
Osservo subito che la nomenclatura di tipo insiemistico, nel caso della probabilità, risulta molto spontanea e funzionale, senza che necessiti di essere introdotta prima in modo specifico.
Aggiungo inoltre che per rispondere alle prime due domande del testo il grafo ad albero non è certo necessario: basta osservare i dati per rispondere immediatamente, con il semplice rapporto fra “numero dei casi favorevoli” e “numero dei casi possibili”. È tuttavia interessante avere sotto gli occhi la schematizzazione proposta, che risulta ben più utile per la successiva domanda.
Poiché si prevede una seconda estrazione senza reimmettere la pallina estratta nel sacchetto (cioè senza reimbussolamento), la situazione può essere facilmente schematizzata così:
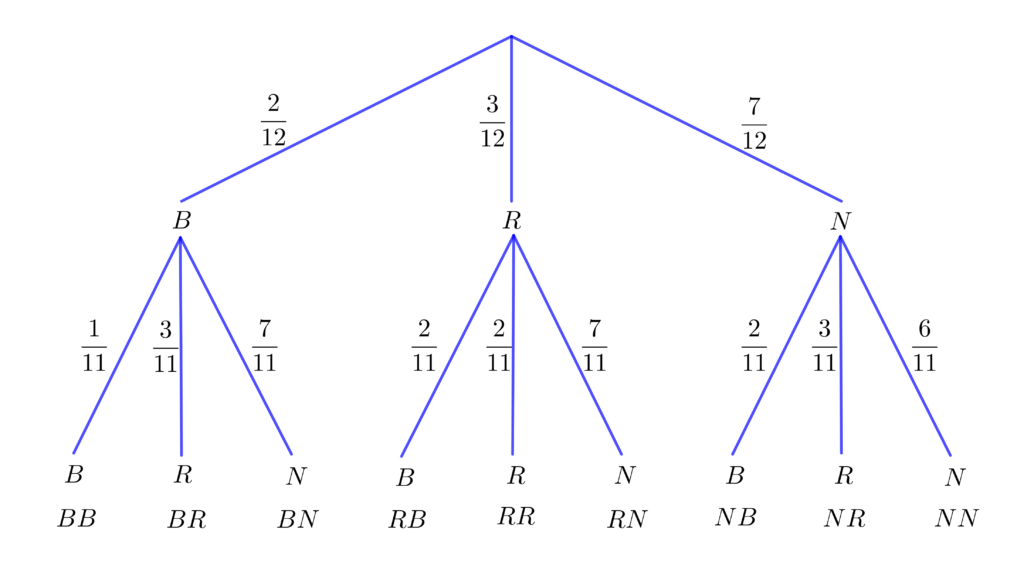
Questa volta i rami del grafo diventano $9$, ciascuno dei quali formati da tre rami “più piccoli”, sui quali è scritta la probabilità dell’evento elementare rappresentato; alla fine di ciascuno di essi si può scrivere, in simboli, l’evento che quel ramo rappresenta: $BB$, per esempio, significa che alla prima estrazione si è avuta una pallina bianca e anche alla seconda estrazione si è pescata ancora una pallina bianca (si tratta dell’evento $B\cap B$). Ma perché moltiplicare le due frazioni scritte lungo i rami per calcolare $p\left( BB\right)$? Si tratta di un tipo di ragionamento che gli alunni hanno già incontrato in più occasioni e di cui è importante renderli consapevoli, cioè il seguente: alla prima estrazione, dire che $p\left( B\right) =\dfrac{1}{12}$ significa che in quella percentuale di casi si ha l’estrazione della pallina bianca; alla seconda estrazione, ammesso che la prima pallina sia bianca, si ha che $p\left( B\right) =\dfrac{1}{11}$ ma questa volta la percentuale dei casi non è sulla totalità dei casi, ma solo sui $\dfrac{2}{12}$ dei casi, dunque l’uscita di questa seconda pallina bianca avviene in una percentuale di casi data da $\dfrac{1}{11}\cdot \dfrac{2}{12}=\dfrac{2}{132}$. E analogamente si calcolano le probabilità degli altri eventi. Si tratta dunque dello stesso tipo di ragionamento che si incontra quando occorre calcolare la frazione di una frazione, o la percentuale di una percentuale ed è importante che gli alunni colgano questa analogia.
È evidente, quindi, per rispondere alla domanda c) del problema, che $p\left( NN\right) =p\left( N\cap N\right) =\dfrac{42}{132}$ e il grafo proposto può suggerire a voi insegnanti di aggiungere altre domande, anche più complesse, cui rispondere facilmente in base alla comprensione e all’utilizzo dello schema costruito.
Nel mio successivo intervento vedremo ancora una situazione schematizzabile con un grafo ad albero, con il commento ad alcuni errori che potrebbero mettere in luce fraintendimenti su cui discutere, nell’ottica di offrire agli alunni occasioni e strumenti che possano arricchire il loro pensiero critico.
1Anche se non è necessario per il problema che propongo qui, ricordo che se $A$ e $B$ sono due eventi, e $B$ è un evento con probabilità maggiore di $0$, cioè con $p\left( B\right) >0$, si dice probabilità condizionata di $A$ dato l’evento $B$, e si scrive $p\left( A| B\right)$, il rapporto: $p\left( A| B\right) =\dfrac{p\left( A\cap B\right) }{p\left( B\right) }$. Ricordo che l’evento $A\cap B$ indica che gli eventi $A$ e $B$ si verificano contemporaneamente.
$A$ e $B$ si dicono eventi indipendenti se $p\left( A\cap B\right) =p\left( A\right) \cdot p\left( B\right) $ e in questo caso si ha $p\left( A| B\right) =p\left( A\right)$ e $p\left( B| A\right) =p\left( B\right)$; intuitivamente, ciò accade se il verificarsi di uno di essi non influenza il verificarsi o meno dell’altro. Nel problema che propongo qui, e in molti altri analoghi, il contesto chiarisce subito se si tratta di eventi indipendenti oppure no.
