
Ciò che vi propongo in questo articolo è un problema piuttosto usuale, analogo a quesiti presenti in Prove INVALSI o nei testi scolastici, tuttavia ve lo presento qui con l’obiettivo di esplorare tutta la sua potenzialità nel promuovere nei ragazzi la ricerca di differenti rappresentazioni di dati, per scoprire dunque quanto possa essere utile sia saper scegliere che saper gestire tali rappresentazioni.
Ricordiamoci quanto sia importante, per sviluppare un atteggiamento consapevole e non meccanico nei ragazzi, riuscire a spostare la loro attenzione dalla semplice ricerca della soluzione corretta di un problema alla capacità di schematizzarne i dati in modi differenti, facilmente collegabili, poi, a strategie risolutive differenti. Avere a disposizione più rappresentazioni, generative di più procedure risolutive per i problemi, consente di arricchire le strategie di pensiero dei nostri alunni e questo, ovviamente, non solo a favore della Matematica ma più in generale per una loro educazione ad ampio raggio.
Ecco dunque il testo dell’attività, che come al solito vi consiglierei di assegnare in collaborazione tra pari, a coppie o a piccoli gruppi, e che si adatta sia all’attività in presenza che a quella a distanza. La raccolta che poi farete, insieme, delle differenti schematizzazioni e procedure risolutive diventerà oggetto di discussione collettiva (se a distanza durante la modalità sincrona), da condividere come esito finale di tutta l’attività.
Un confronto di tariffe
Andrea e Bruno frequentano la stessa palestra ma con modalità di pagamento diverse:
- Andrea paga una quota fissa mensile di $12$ euro più $2,50$ euro per ogni presenza;
- Bruno ritiene sia più conveniente pagare $3$ euro per ogni presenza effettiva.
Entrambi frequentano assiduamente la palestra e giungono alla conclusione che, per un determinato numero di presenze, la scelta della modalità di pagamento è del tutto indifferente.
Siete d’accordo? Giustificate in dettaglio la vostra risposta, descrivendo come avete ragionato e aggiungendo anche vostre osservazioni.
Come è evidente, il problema è espresso solo verbalmente e il ricorso a eventuali schematizzazioni dei suoi dati non è esplicitamente richiesto. Tuttavia di solito per descrivere in dettaglio il ragionamento svolto per argomentare la risposta e per proporre osservazioni gli studenti utilizzano schemi, tabelle o grafici che possano mettere in evidenza lo svolgimento della loro procedura. Se preferite, potreste richiedere esplicitamente agli alunni di schematizzare i dati nel modo che ritengono più opportuno per giustificare meglio la loro risposta, così da potervi assicurare una raccolta significativa di rappresentazioni.
Vediamo dunque quali strategie risolutive potrebbero scaturire dalla considerazione dei dati forniti dal testo per il confronto delle due tariffe.
È chiaro che se il problema è proposto in una classe terza della secondaria di primo grado, quando gli alunni hanno già un po’ di familiarità con equazioni di primo grado, o nel biennio del secondo grado, può essere immediato indicare, per $n$ ingressi in palestra, con $12+2,5n$ la spesa in euro di Andrea e con $3n$ quella di Bruno. È evidente che se l’equazione $12+2,5n=3n$ ha soluzione intera, allora si può rispondere positivamente alla domanda del testo. In effetti la soluzione è $n=24$ e dunque per $24$ ingressi la scelta di una delle due modalità di pagamento è indifferente: entrambi pagano infatti $72$ euro.
Un altro modo di ragionare e che porta ovviamente alla stessa soluzione è il seguente: se prescindiamo dai $12$ euro iniziali previsti dalla tariffa di Andrea, a ogni ingresso Bruno paga $50$ centesimi più di Andrea e dunque quando questi centesimi raggiungeranno i $12$ euro pagati da Andrea, i loro costi saranno uguali: dunque $0,50n=12$, cioè con $n=24$ ingressi le due modalità di pagamento risultano indifferenti (e la soluzione $n=24$ è immediata, al di là del saper gestire un’equazione!)
Eventuali osservazioni sulle due modalità di pagamento proposte emergono però più facilmente se si procede per esempio con una strategia più ingenua, elencando passo passo i costi che devono sostenere Andrea e Bruno, rispettivamente, all’aumentare del numero di ingressi. Si potrebbe dunque costruire una tabella di questo tipo:
| N° ingressi | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | … |
| Costo per Andrea (in euro) | $12+2,5=14,5$ | $17$ | $19,5$ | $22$ | $24,5$ | $27$ | … |
| Costo per Bruno (in euro) | $3$ | $6$ | $9$ | $12$ | $15$ | $18$ | … |
Nel compilare la tabella emergono subito alcune osservazioni, per esempio che Bruno paga in ogni caso un numero intero di euro, mentre Andrea paga un numero intero di euro solo per un numero pari di ingressi, dunque se si vuole scoprire se le due modalità di pagamento sono indifferenti, si potrà considerare solo il caso di un numero pari di ingressi. Inoltre, procedendo per tentativi, si può provare a calcolare i costi nei casi di $10$, $20$ o $30$ ingressi, per poter vedere quando i due costi sono più vicini:
| N° ingressi | $10$ | $20$ | $30$ | … |
| Costo per Andrea (in euro) | $37$ | $62$ | $87$ | … |
| Costo per Bruno (in euro) | $30$ | $60$ | $90$ | … |
Un’altra osservazione risulta ora evidente: fino a $20$ ingressi Andrea paga sempre più di Bruno ma per $30$ ingressi è Bruno che paga di più, dunque occorre esplorare meglio la situazione tra $20$ e $30$ ingressi e si arriva in breve a scoprire che per $24$ ingressi entrambi i ragazzi pagano $72$ euro.
Un’ulteriore strategia risolutiva è quella che ricorre alla rappresentazione, nel piano cartesiano, delle due rette che rappresentano i costi delle due tariffe.
Se sull’asse $x$ si rappresenta il numero degli ingressi in palestra e sull’asse $y$ il costo, in euro, delle rispettive tariffe, si ha
- per Andrea, la retta $f$, di equazione $y=2,5x+12$;
- per Bruno la retta $g$, di equazione $y=3x$.
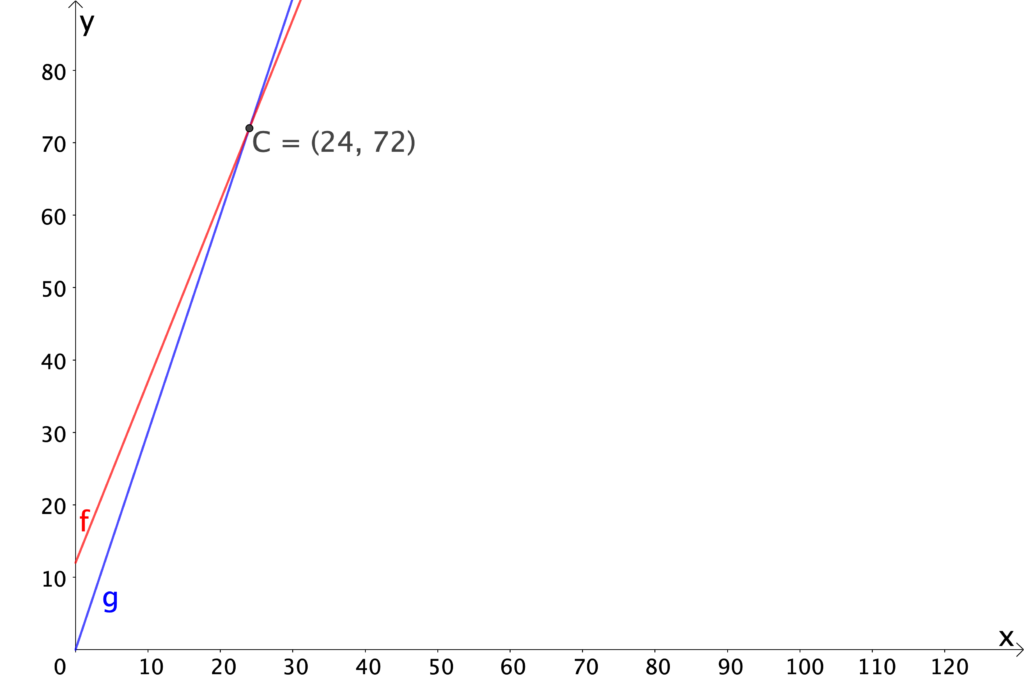
Il punto di intersezione tra le due rette identifica quando queste tariffe “si incontrano”, cioè quando Andrea e Bruno pagano la stessa somma di denaro. Le coordinate di questo punto di intersezione dicono esattamente quando questo avviene, cioè per $24$ ingressi, cui corrisponde il costo di $72$ euro.
Un’interessante osservazione da fare, relativamente all’uso di questa strategia, è collegabile al fatto che le rette $f$ e $g$ sarebbero da considerare rette “di punti”, perché, per la situazione che vogliamo considerare, in cui ha senso parlare solo di numeri interi (e positivi) di ingressi, il ricorso a rette “piene” è persino eccessivo, tuttavia i loro grafici mettono bene in risalto che per un numero di ingressi minore di $24$ è Bruno a pagare di meno, per $n=24$ i due ragazzi pagano lo stesso importo e per un numero di ingressi maggiore di $24$ è Andrea a pagare di meno.
Un’osservazione, infine, che può essere opportuna al di là della strategia risolutiva scelta, è che poiché il testo del problema parla di quote mensili e il mese consta di $31$ giorni al massimo, la tariffa più conveniente è probabilmente quella scelta da Bruno, perché solo per un numero di ingressi superiori a $24$ pagherebbe più di Andrea: anche se entrambi molto sportivi, si può pensare infatti che non frequentino la palestra tutti i giorni del mese, prevedendo per esempio qualche giorno di vacanza fuori sede oppure qualche giorno di influenza o di studio intenso… L’interpretazione del risultato nel contesto assegnato è sempre interessante, proprio per tradurre nella realtà proposta ciò che si è ottenuto numericamente, valutandone appieno il significato e dando un senso a ciò che si è svolto.
In riferimento alle rappresentazioni descritte, possiamo dire in conclusione che anche quando fosse accessibile ai ragazzi la soluzione algebrica, favorire la presentazione dei dati del problema in una tabella o in un grafico può essere molto utile, come abbiamo visto, per un’osservazione dei dati più puntuale, per la generazione e il confronto di strategie differenti, per la formulazione di osservazioni e per la loro argomentazione, insomma per un arricchimento significativo di strategie di pensiero.
