
Purtroppo ci risiamo… di nuovo davanti a uno schermo, privati del guizzo di umanità che, nel bene o nel male, ci comunicano i volti addormentati, sorpresi, annoiati o sconfortati dei nostri studenti. Ma quello che più manca è la possibilità di interagire, di confrontarsi, di collaborare e di discutere. E proprio per questo qualsiasi strumento o attività che possa aiutare noi e i nostri studenti a recuperare questi momenti di “socialità scolastica” è estremamente prezioso.
Il gioco che vi propongo va in questa direzione e permette di fare un ripasso di geometria analitica unendo matematica ed enigmistica e stimolando al tempo stesso la discussione tra i ragazzi. Inoltre, il gioco fornisce una buona occasione per far conoscere ai vostri studenti qualche strumento di scrittura collettiva e collaborativa.
Per prepararlo potete utilizzare un qualsiasi schema di “parole intrecciate” facilmente reperibile in rete o su una qualunque rivista di giochi enigmistici. Una volta scelto lo schema che vi piace, come prima cosa aggiungete alla vostra griglia di lettere un sistema di coordinate cartesiane in modo tale che ogni lettera nello schema sia identificata da una coppia di numeri. A seconda della classe in cui volete proporre il gioco e del livello dei vostri studenti potete mettere l’origine nell’angolo in basso a sinistra, oppure, come mostrato in questo esempio, in un punto a caso della griglia.
A questo punto associate a ogni parola il segmento che le corrisponde, identificandolo come un tratto di retta. Per esempio, nello schema seguente, la parola OCA corrisponde a $y=x+1$ con $x\in\left[-2,0\right]$, la parola APE a $x=0$ con $y\in\left[-1,1\right]$ e la parola RANE a $y=x-1$ con $x\in\left[0,3\right]$.
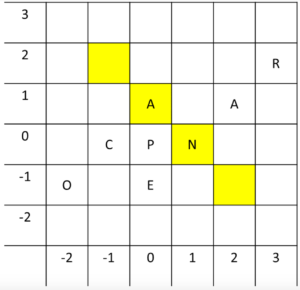
Naturalmente il segmento descrive semplicemente la posizione della parola nella griglia, ma non fissa in nessun modo il verso in cui la parola va inserita in tale posizione: infatti il verso dovrà essere stabilito a posteriori in modo da rispettare tutti i possibili intrecci. Per esempio, se a questo punto dovessimo posizionare la parola CANE in corrispondenza del segmento identificato da $y=1-x$ con $x\in\left[-1,2\right]$, le lettere già presenti nello schema rendono obbligatorio inserirla nelle caselle gialle con un verso che va dall’alto verso il basso. A seconda della classe in cui state proponendo l’attività potete decidere di dare le equazioni delle rette in forma “pulita”, oppure di complicare leggermente il gioco scrivendo le equazioni in forma meno esplicita. Per esempio, nello schema precedente alla parola RANE potreste decidere di far corrispondere la retta di equazione $4y+1=4x-3$ con $x\in\left[0,3\right]$.
Per giocare dividete la classe in squadre (formate da $3$ o $4$ giocatori ciascuna) e date a ogni squadra uno schema nel quale compaiono solamente i numeri che servono a identificare i quadretti della griglia e la lista delle parole da inserire con a lato l’indicazione delle relative posizioni.
Scopo del gioco è posizionare correttamente tutte le parole nel minor tempo possibile. Attenzione: nel caso nel vostro schema ci fossero alcune caselle nelle quali non va inserita nessuna lettera, ricordatevi di colorarle in modo tale che, una volta inserite tutte le parole, lo schema risulti completamente riempito. Questo da un lato consentirà a voi una più immediata verifica della correttezza o meno della soluzione proposta e dall’altro permetterà agli studenti di accorgersi di eventuali errori qualora una delle parole inserite vada a sovrapporsi a una casella colorata.
Per utilizzare il gioco a distanza basterà che voi docenti salviate la griglia vuota e le parole da inserire con le relative indicazioni per il loro posizionamento come immagini e le incolliate su un documento utilizzabile per la scrittura collaborativa (per esempio Presentazioni Google oppure Jamboard). Così facendo non si corre il rischio che alcune parole o lettere vengano cancellate per sbaglio dai ragazzi, soprattutto nel caso siano alle prime armi con questo tipo di strumenti digitali. Una volta creato il documento, ne farete tante copie quante sono le squadre in modo tale che, dopo aver spiegato il gioco e formato le squadre, sarà sufficiente condividere con ogni squadra il link alla copia corrispondente.
In questo modo tutti i giocatori di una stessa squadra si troveranno a condividere lo stesso tabellone, sul quale potranno agire simultaneamente posizionando le diverse parole. Naturalmente durante la partita gli studenti di una stessa squadra potranno consultarsi in tutti i modi possibili, aprendo una riunione su Zoom, parlando tra loro su WhatsApp o in uno degli altri mille modi in cui sono abituati a comunicare quotidianamente tra loro!
Quando una squadra è convinta di avere posizionato correttamente tutte le parole, basterà che salvi il file finale in formato PDF e che lo invii all’insegnante. Vince la squadra che invia per prima il tabellone completato, a patto che tutti gli incroci siano rispettati e che tutte le parole siano state inserite.
Vuoi un gioco già fatto? Vai in Zona Matematica, nell’area dedicata al Gioco.
Per il primo grado
Per il secondo grado – I biennio
