Da alcuni anni cerco di rendere la matematica più tangibile agli studenti (dagli alunni di scuola primaria a quelli universitari) ricorrendo all’antica arte della piegatura della carta: l’origami. Questa scelta è motivata da vari fattori. Prima di tutto le pieghe origami sono state assiomatizzate: alcune di essi sono confrontabili con le costruzioni con riga e compasso di Euclide ma una, in particolare, rende questo sistema assiomatico più ricco di quello con riga e compasso, permettendo anche la soluzione di problemi classici come la trisezione dell’angolo e la duplicazione del cubo. Inoltre, negli ultimi anni, importanti università e centri di ricerca stanno rifacendosi a quest’arte per le sue potenzialità nelle applicazioni tecnologiche.
Quindi l’utilizzo dell’origami in classe permette un approccio diverso, più concreto e motivato alla matematica, correttamente formalizzato.
Vorrei allora proporre un argomento curricolare che potrete riprodurre facilmente nella vostra classe.
Avete mai piegato un teorema di trigonometria? Per chi volesse cimentarsi ecco le istruzioni per dimostrare, piegando, il teorema di duplicazione del seno. Io l’ho imparato dal matematico Tom Hull, ospite del CDO (Centro Diffusione Origami) in Italia nel Novembre 2012.
Osserviamo che in generale, nei libri di testo, questo teorema si ricava dalla formula di addizione, mentre qui la ricaveremo direttamente.
Dato un angolo β, con
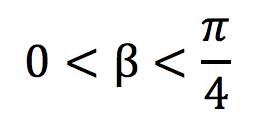
dobbiamo dimostrare che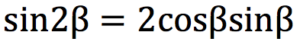 
Distribuite ai vostri studenti, uno per ciascuno, un triangolo rettangolo di carta; può essere comodo ricavarlo dividendo fogli A4 lungo la diagonale. Chiamate A, B e C i vertici del triangolo rettangolo in modo che C e A siano gli estremi dell’ipotenusa.
Date ora le seguenti istruzioni di piegatura, che mostrerete sul vostro modello alla classe e che ogni alunno ripeterà sul suo triangolo di carta.
Ovviamente le proprietà degli elementi geometrici che via via appaiono (asse del segmento, triangolo isoscele, angolo supplementare) devono essere discusse e motivate dagli studenti.
1- Portare il vertice C sul vertice A e piegare (Figura 1); la piega rappresenta l’asse del segmento AC e interseca in P il cateto BC e in H l’ipotenusa AC.
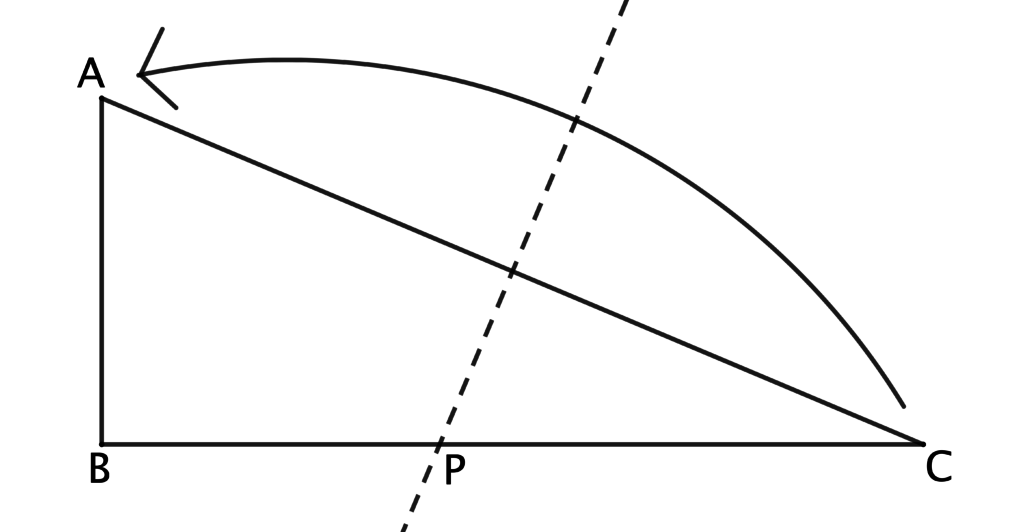
FIGURA 1
(Il movimento origami che porta parte di un segmento su se stesso produce sempre una piega perpendicolare al segmento stesso; se si porta un vertice del segmento sull’altro, la piega passa anche dal punto medio e diventa quindi l’asse del segmento).
2- Piegare il triangolo sul segmento AP (Figura 2): non è necessario riaprire la piega precedente: ci si può appoggiare sullo strato di carta appena piegato. Il triangolo APC è isoscele.
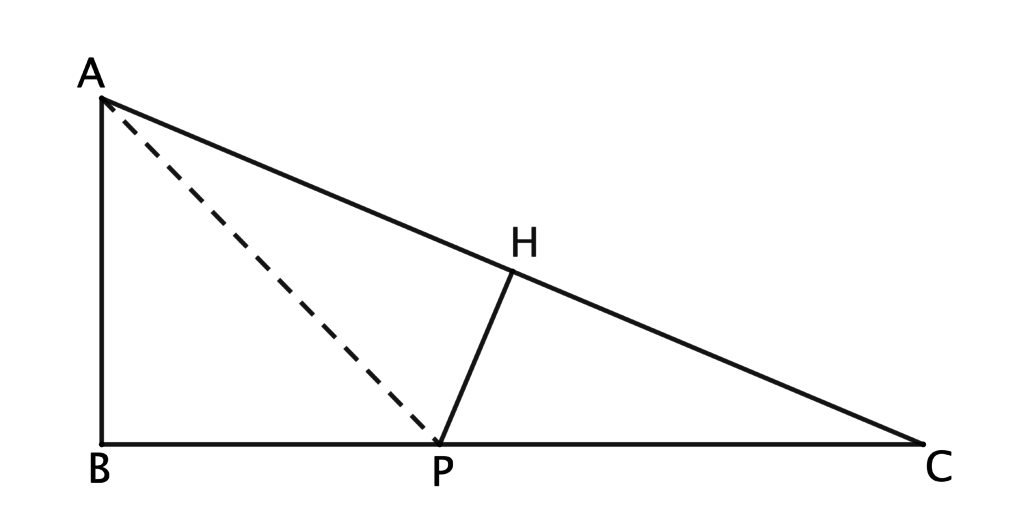
FIGURA 2
(Nella piega descritta nel punto precedente, il segmento CP è stato sovrapposto ad AP e quindi essi risultano congruenti).
3- Poniamo
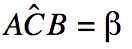e supponiamo
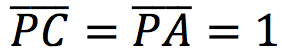
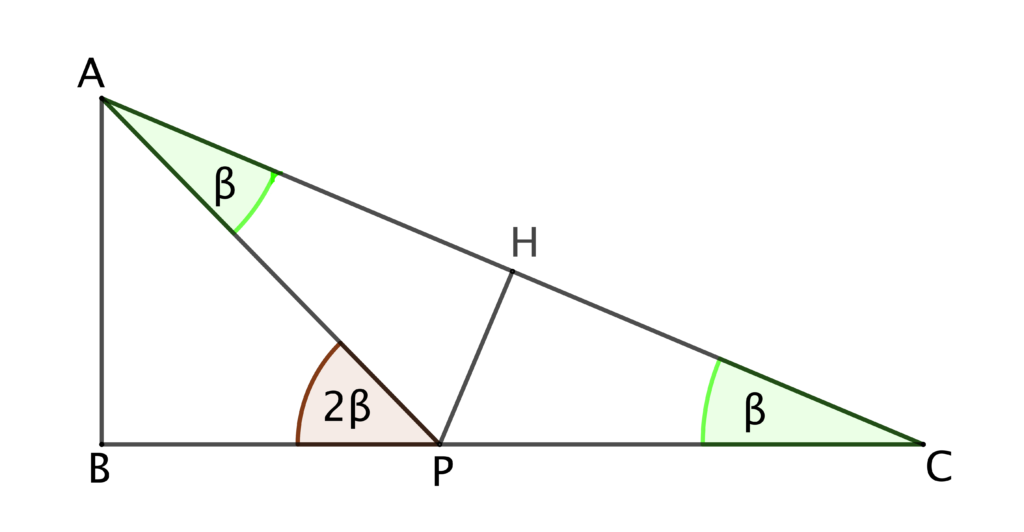
FIGURA 3
L’angolo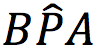 
è supplementare a 
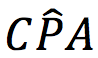ed è dunque congruente a 2β.
Abbiamo allora che:
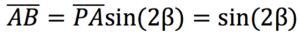
e anche
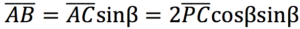
da cui
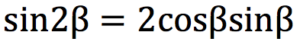
Poter toccare con le proprie mani la dimostrazione darà una grande soddisfazione ai vostri ragazzi!
Si potrà poi chiedere di dimostrare la formula della duplicazione del coseno, lasciando lavorare gli studenti da soli, a coppie oppure in gruppo.
Buone pieghe!
———————————————————————————————————————————–
La professoressa Spreafico vi aspetta ai convegni “Motivare Coinvolgere Divertire con la Matematica” con il laboratorio Piega, spiega e apprendi: origami in matematica.