
I legami tra musica e matematica sono molto antichi, la bibliografia a riguardo ne è la testimonianza ed è molto vasta. Il nostro scopo, in questo articolo, non è parlare di questi legami ma di farne esperienza, proponendo i laboratori “Doremat”, una pratica didattica nata da un progetto di ricerca (una descrizione degli aspetti didattici del progetto si può leggere qui).
Un’espressione aritmetica può avere un suono? Possiamo immaginare di ascoltare o suonare $\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{2}{8}$?
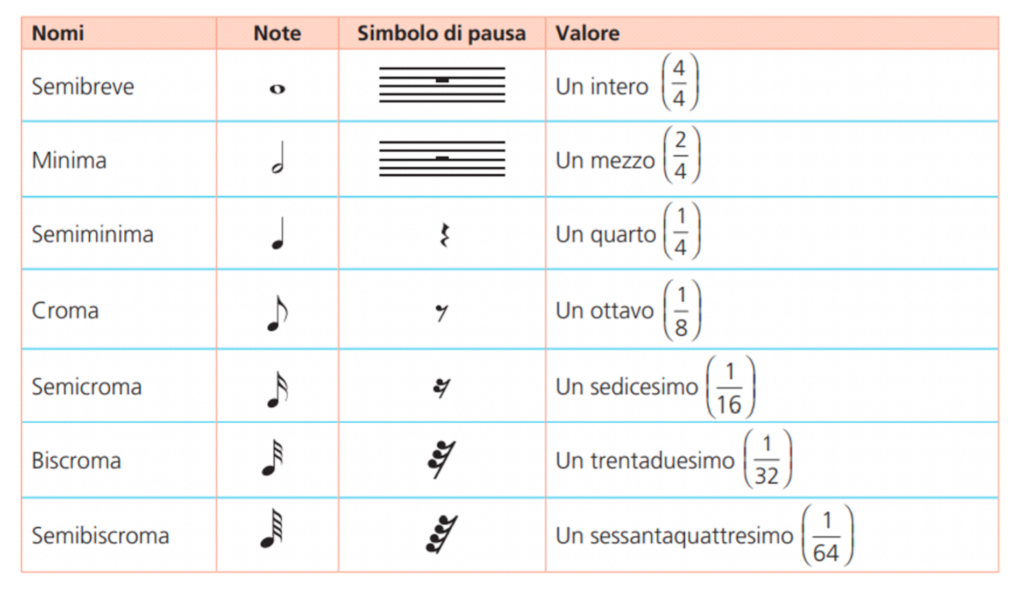
In effetti, oltre a immaginarlo possiamo proprio realizzarlo! Basti pensare al fatto che, in musica, le durate delle note vengono indicate anche con frazioni, come mostra la seguente tabella.
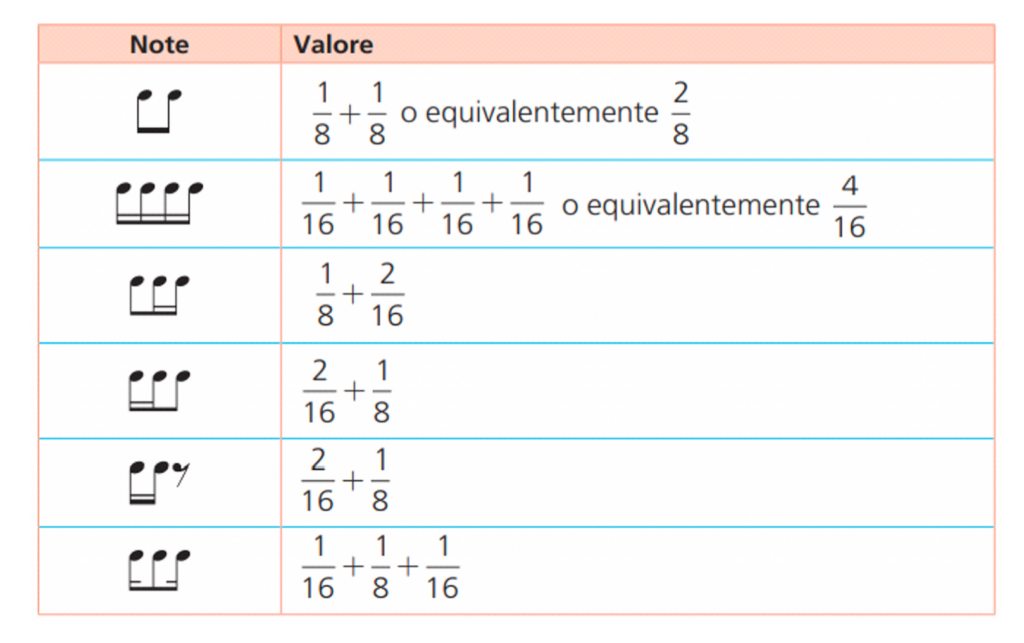
Note di diversa durata possono essere raggruppate a formare ritmi. Ne vediamo alcuni esempi nella Tabella 2.
Le note musicali sono caratterizzate da due aspetti: la durata e l’altezza (quest’ultima viene identificata attraverso la scrittura delle note su un pentagramma, precedute da una “chiave” musicale di lettura, come per esempio la chiave di violino, che specifica come vanno lette quelle note). In questo primo articolo ci serviremo soltanto della durata delle note e della loro organizzazione in un brano musicale. L’esposizione che segue è divisa in tre parti, ciascuna delle quali contiene attività e schede di lavoro per gli studenti; la suddivisione ha lo scopo di ripartire gli argomenti che verranno trattati, per una fruizione e una lettura più chiare.
Parte prima: frazioni e figure ritmiche
In riferimento alla tabella 1, e scorrendola dall’alto verso il basso, osserviamo che il rapporto tra le durate di due figure ritmiche consecutive è sempre di $2:1$, il rapporto diviene di $1:2$ se si scorre la tabella dal basso verso l’alto. Per esempio, la durata della semibreve è il doppio della durata della minima (rapporto $2:1$), la croma dura la metà della semiminima (rapporto $1:2$) e così via. Possiamo dunque proporre ai nostri allievi una prima attività al fine di comprendere i rapporti di durata che sono stabiliti tra le figure ritmiche, nonché i rapporti tra grandezze variabili e la rappresentazione di tali rapporti in forma aritmetica, ossia attraverso i numeri. Qui potete scaricare l’attività e la relativa scheda di lavoro per gli studenti.
Parte seconda: espressioni aritmetiche e battuta musicale
Il tempo in cui si svolge la vicenda sonora è suddiviso in porzioni di tempo, chiamate battute; ogni battuta, a sua volta, organizza il tempo in modo vario in base al metro. Utilizziamo qui, per semplicità, il metro $\dfrac{4}{4}$: posto all’inizio del brano indica che in ciascuna battuta deve essere contenuto un valore totale di $\dfrac{4}{4}$, mescolando variamente note, pause e figurazioni ritmiche.
Queste che vedete di seguito sono battute musicali.

Come facciamo a sapere che la battuta è di $\dfrac{4}{4}$? Tendenzialmente, contiamo i quarti e spontaneamente eseguiamo un’addizione tra quarti: l’addizione è basata sull’atto del contare e, semplificando, possiamo dire che contare significa addizionare e che addizionando si conta. Abbiamo quindi operato i seguenti collegamenti: ad alcune figure ritmiche (o raggruppamenti ritmici) abbiamo associato alcune frazioni e alla concatenazione di figure ritmiche (o raggruppamenti ritmici) abbiamo associato l’addizione tra frazioni. Una battuta musicale, come detto poc’anzi, può essere formata da varie note, pause e figurazioni ritmico-melodiche ottenute dalla combinazione di note e pause, per esempio così (in tal caso sono solo figurazioni ritmiche, non ci sono pause):

Tenendo conto delle associazioni che abbiamo operato, la rappresentazione aritmetica di questa battuta è la seguente:
$\dfrac{2}{8}+\dfrac{1}{4}+\dfrac{4}{16}+\dfrac{1}{4}$
Il risultato di tale espressione, non a caso, è proprio $1$, ossia il numero di battute da $\dfrac{4}{4}$.
Sulla base delle precedenti osservazioni possiamo proporre ai nostri studenti le attività e le schede di lavoro che potete scaricare qui, insieme all’audio dell’esempio 1 e all’audio dell’esempio 2.
Parte terza: espressioni aritmetiche e sequenze ritmiche
Fino a ora abbiamo composto e suonato singole battute di metro $\dfrac{4}{4}$; ora ampliamo un po’ il discorso per comporre e suonare sequenze ritmiche, ossia per mettere insieme varie battute musicali. Prendiamo per esempio la seguente sequenza ritmica, formata da tre battute di metro $\dfrac{4}{4}$:

Coerentemente con quanto prima esposto, una sua rappresentazione aritmetica potrebbe essere la seguente:
$\dfrac{2}{8}+\dfrac{1}{4}+\dfrac{4}{16}+\dfrac{1}{4}+\dfrac{4}{16}+\dfrac{2}{8}+\dfrac{4}{16}+\dfrac{2}{8}+\dfrac{1}{2}+\dfrac{4}{16}+\dfrac{1}{4}$
oppure, considerando la ripetizione in successione di due figurazioni nella seconda battuta, la seguente:
$\dfrac{2}{8}+\dfrac{1}{4}+\dfrac{4}{16}+\dfrac{1}{4}+\left( \dfrac{4}{16}+\dfrac{2}{8}\right) \times 2+\dfrac{1}{2}+\dfrac{4}{16}+\dfrac{1}{4}$
Calcoliamo il risultato dell’espressione: è $3$, ossia il numero di battute da $\dfrac{4}{4}$ che compongono la nostra sequenza.
A questo punto, le attività che possiamo svolgere in classe sono numerose: dall’esecuzione individuale di una sequenza ritmica all’esecuzione della stessa accompagnata da più voci; dalla rappresentazione in notazione aritmetica di una sequenza ritmica e dal calcolo di un’espressione a una problematizzazione della stessa rappresentazione (per esempio, l’addizione è un’operazione commutativa? Possiamo dire lo stesso della concatenazione delle figure ritmiche?)
Qui potete scaricare alcune attività e schede di lavoro, insieme all’audio dell’esempio 1 e all’audio dell’esempio 2.


