
Eccoci in forma e carichi per un nuovo anno scolastico!
Proviamo a coinvolgere da subito i nostri studenti con un’attività stimolante che li renda curiosi e ben predisposti alle nuove avventure matematiche che proporremo quest’anno.
Chi di voi ha assegnato i compiti delle “Vacanze poliedriche” può usare l’attività che ora vi propongo per concludere la correzione dei compiti (attività 4). Chi non li ha assegnati è ancora in tempo a utilizzarli per il ripasso oppure può svolgere questa proposta come lezione indipendente.
Faremo piegare ai ragazzi semplici poliedri e li metteremo sulle tracce della bella formula di Eulero che coinvolge il numero di vertici, spigoli e facce. L’attività si presta anche per gli studenti della primaria, una volta che avremo definito i termini vertice, spigoli e facce.
Innanzitutto, ogni studente piegherà almeno tre moduli seguendo le istruzioni che trovate nell’articolo “Vacanze poliedriche”. Per comodità riporto il diagramma di piegatura.
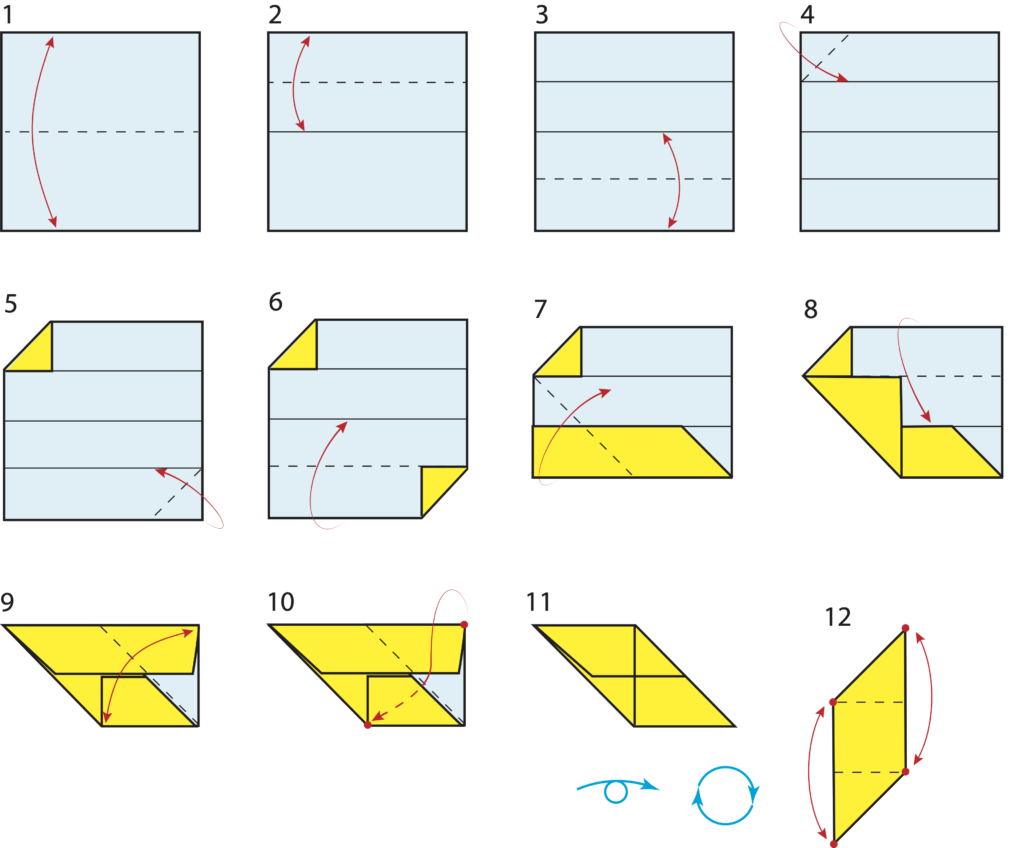
La figura finale è formata da un quadrato centrale (che ospita delle tasche) e due triangoli che chiameremo alette.
Ora potete usare le spiegazioni che seguono per costruire un poliedro a $6$ facce (doppio tetraedro non regolare o doppia piramide a base triangolare).

1) Piegate tre moduli e disponeteli come in figura.

2) Ruotate di $90°$ il modulo centrale e infilate la sua aletta di sinistra nella tasca del primo modulo, che si trova in corrispondenza della metà inferiore della diagonale del quadrato uscente dal vertice in basso a destra.

3) Inserite ora l’aletta in alto del terzo modulo nella tasca formata dalla metà diagonale in basso a sinistra del secondo modulo.

4) Completate l’incastro dei tre moduli inserendo l’aletta in basso del primo modulo nella metà diagonale superiore sinistra del terzo modulo. Il modello acquisterà tridimensionalità.

5) Ribaltate la figura, ottenendo il modello mostrato in figura.

6) Ora completate il modello incastrando le alette in senso antiorario: l’aletta del modulo $1$ (in giallo) va inserita nel modulo $2$ (in arancione); l’aletta del modulo $2$ va inserita nel modulo $3$ (in verde) e, infine, quella del modulo $3$ va inserita nel modulo $1$. Si otterrà il poliedro a sei facce della figura.
Osservazione: arrivati al passaggio 4, possiamo notare che il modello “alette escluse” può essere visto come porzione di cubo (un vertice, tre spigoli e tre mezze facce). È semplice completare il cubo piegando altri tre moduli.
In questo modo i ragazzi avranno a disposizione due poliedri.
Potete ora guidarli alla scoperta della formula di Eulero, utilizzando la scheda che trovate in Zona Matematica. L’attività può essere proposta già dalle ultime classi della scuola primaria. Nella scuola secondaria di primo e secondo grado si potranno aggiungere anche considerazioni su superfici totali, volumi e solidi platonici.
Buon rientro a tutti!
In Zona Matematica, nell’area dedicata agli origami, potete trovare i materiali di supporto all’attività.
Vai all’area “Origami” del I grado
Vai all’area “Origami” del II grado – I biennio
Vai all’area “Origami” del II grado – II biennio e V anno
