Si avvicina Natale e al Polo Nord fervono i preparativi: gli elfi sono al lavoro per impacchettare i doni, Babbo Natale legge le lettere che arrivano da tutto il mondo e le renne si allenano in vista del viaggio nella notte di Natale.
Come tutti sanno, oltre ai doni, va trasportata nella notte della vigilia anche la polvere di stelle, indispensabile da spargere a ogni ripartenza dai tetti delle case.
Ma quest’anno è sorto un problema. L’elfo Hardil ha piegato una scatola partendo da un foglio A$3$ e seguendo queste istruzioni 1:
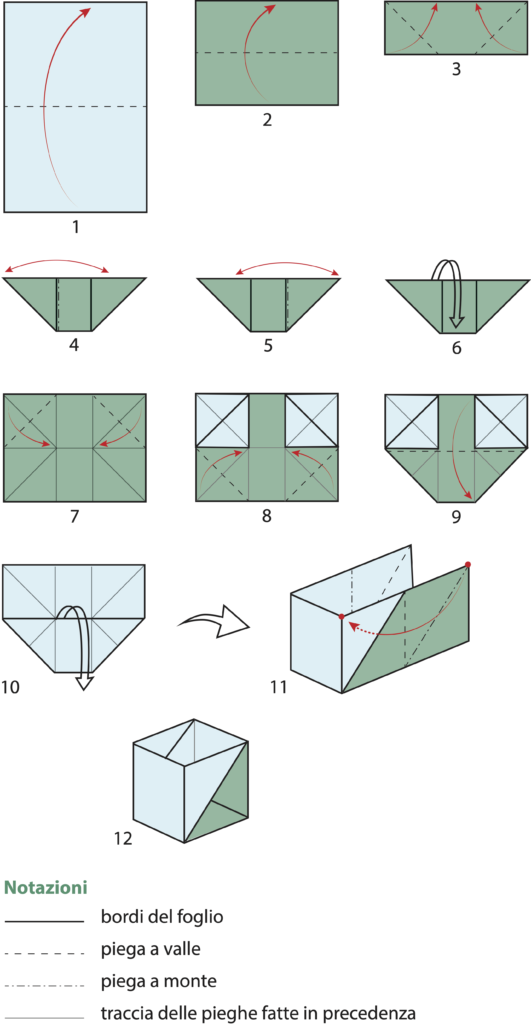
Ha riempito fino all’orlo la scatola con la polvere di stelle e l’ha consegnata alla renna Rodolfo, che dovrà trasportarla al collo per prelevare via via la polvere da spargere durante i decolli dai tetti delle case. Rodolfo però ha fortemente protestato perché non vuole essere l’unico a portare e spargere la polvere e chiede ad Hardil di piegare un certo numero di scatole più piccole, nelle quali distribuire tutta la polvere di stelle che ora è nella scatola grande, in modo da ripartirle a diverse renne.
Vogliamo aiutare Hardil a soddisfare la richiesta di Rodolfo?
L’aiuto ad Hardil può essere strutturato in un’attività prenatalizia da svolgere in classe o da assegnare come compito delle vacanze.
Chiedete ai vostri studenti di immaginare di dover distribuire la polvere di stelle da un’unica scatola in scatole più piccole, prevedendo inizialmente il numero di scatole piccole che occorreranno. Chiedete loro di confermare o cambiare la previsione alla luce di osservazioni che li guiderete a fare durante l’attività. Loro stessi poi verificheranno la loro proposta di soluzione… con i fatti: piegheranno le scatoline e le inseriranno nella scatola, fino a occuparla completamente. In questo modo, grazie alla polvere di stelle, la relazione tra lati, aree e volumi non avrà più segreti.
L’attività non richiede la conoscenza di nessuna formula e può essere assegnata dagli $8$ ai $14$ anni.
Se gli studenti non hanno a disposizione un foglio A$3$, possono unire due fogli A$4$ o utilizzare un foglio di protocollo aperto.
Ecco una possibile sequenza di domande.
- Hardil ha deciso di dividere in quattro parti, lungo gli assi di simmetria, alcuni fogli A$3$ e di ripetere la costruzione indicata sopra con fogli più piccoli di questa dimensione. Senza tagliare il foglio A$3$, Hardil vorrebbe sapere quante scatole piccole dovrà piegare, per distribuire tutta la polvere di stelle. Secondo te, quante scatole piccole dovrà piegare per travasare tutta la polvere di stelle?
- Procurati ora alcuni fogli A$3$ e tagliali lungo i due assi di simmetria del rettangolo. Ogni rettangolo ottenuto è un A$5$. Che misure hanno i lati di ogni foglio A$5$, rispetto a quelli del foglio A$3$ iniziale? E che relazione c’è tra le aree? Alla luce di queste nuove informazioni, quante scatoline costruite dai fogli A$5$ serviranno per contenere la polvere di stelle della scatola iniziale?
- Piega ora tante scatoline (da fogli A$5$) quante ce ne stanno nella scatola iniziale (piegata con il foglio A$3$). Finalmente ecco la risposta: sappiamo con certezza quante scatoline occorrono per contenere tutta la polvere di stelle!
Osserviamo che, in generale, gli studenti trovano una crescente difficoltà nel capire cosa succede a perimetri, aree e volumi se si dimezzano i lati della figura iniziale. Probabilmente non sarà immediato che tutti gli studenti prevedano subito che occorrono $8$ scatole piccole, dato che, a partire dal foglio A$5$, avremo dimezzato le misure di tutti i lati del parallelepipedo.
Con questa attività avranno modo di riflettere, correggere e infine verificare, costruendo direttamente le scatole piccole e inserendole in quella più grande.
In Zona Matematica è possibile scaricare la scheda di lavoro dell’attività, che può essere proposta come compito delle vacanze di Natale. Nella scheda è presente il diagramma di piegatura della scatola proposta nell’articolo “Che Scatole! Un’attività inclusiva con gli origami” dove, eventualmente servissero, sono dettagliate le istruzioni di piegatura.
Buon Natale!!!
1 La scatola è stata ideata da Giuseppe Baggi (1916-1972), un grande origamista italiano.
In Zona Matematica, nell’area dedicata agli origami, potete trovare una scheda da proporre alla classe e relative soluzioni.
Vai all’area “Origami” del I grado
Vai all’area “Origami” del II grado – I biennio