
Che scatole! Da grido di noia dei nostri studenti a simpatica attività inclusiva che permette di esplorare aree, perimetri e frazioni.
Vi propongo un bel modello di scatola di un grande origamista italiano: Giuseppe Baggi (1916-1972). Tra le pieghe calcoleremo perimetri e aree.
Per piegare la scatola sarà sufficiente che ogni studente abbia un foglio A$4$ bicolore, o più semplicemente potrà decorare una faccia del classico foglio A$4$ bianco, che chiameremo colorata, oppure usare fogli da riciclare con una faccia stampata (colorata) e una bianca.
Qui di seguito trovate il diagramma e le istruzioni di piegatura (nel diagramma, la parte bianca corrisponde alla parte verde e quella colorata alla parte azzurra).
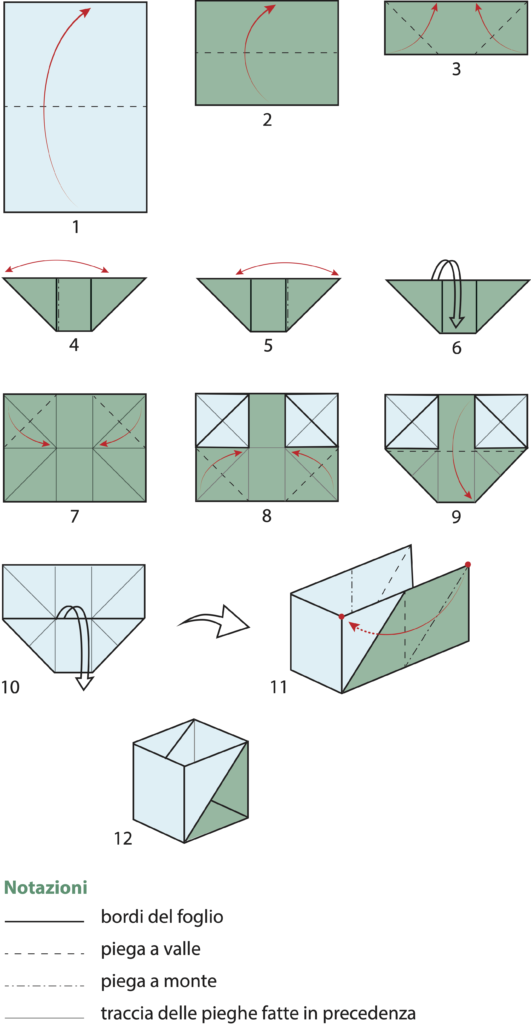
Appoggiare il foglio A$4$ con la parte colorata (o decorata) verso l’alto.
- Piegare lungo la mediana corta, portando il lato corto in basso sul lato corto in lato.
- Il foglio è ora un rettangolo a doppio strato di carta, che presenta i due lati lunghi orizzontali. In basso il doppio strato è unito; verso l’alto i due strati si possono separare. Portare il lato lungo in basso su quello lungo in alto, piegando la mediana lunga di questo nuovo rettangolo.
- Portare i due lati corti sul lato lungo più in alto. Le pieghe forniranno le bisettrici dei due angoli retti più in alto. La figura finale è il trapezio disegnato nel passaggio successivo.
- Piegare a monte un’altezza del trapezio uscente da uno dei vertici della base minore e riaprire. Per eseguire la piega perpendicolare alla base maggiore, aiutarsi sovrapponendo le porzioni di base maggiore.
- Piegare a monte l’altezza del trapezio uscente dall’altro vertice della base minore e riaprire.
- Riaprire le pieghe fatte in 3 e in 2, arrivando al rettangolo ottenuto dopo il passaggio 1, mostrato nel passaggio 7.
- Controllare di avere il lato lungo con doppio strato non separabile verso di sé (cioè in basso). Come mostra la figura del passo 7, le pieghe fatte dividono il rettangolo in quattro quadrati esterni e due rettangoli interni; inoltre sono anche rappresentate dalle pieghe una diagonale per ognuno dei quadrati. Lavorando solo sui due quadrati in alto, e solo su uno strato di carta, piegare le altre loro due diagonali.
- Lavorando sui due quadrati esterni in basso, piegare le altre loro due diagonali, questa volta (obbligati anche dalla carta stessa) muovendo i due strati di carta. La figura che si ottiene è l’esagono non regolare rappresentato nel passaggio 9.
- L’esagono si può vedere come somma di un rettangolo e di un trapezio isoscele, “uniti” lungo il lato lungo del rettangolo e la base maggiore del trapezio. Sul rettangolo poggia uno strato di carta che forma un trapezio bicolore. Piegare questo trapezio sull’altro bianco lungo la comune base maggiore. Si otterrà un esagono tutto colorato.
- Sollevare ora il bordo di carta corrispondente alla base maggiore del trapezio, ottenendo un modello $3$D di scatola aperta rappresentata nella figura del passaggio 11.
- Completare la scatola, piegando a valle e monte come indicato in figura. In particolare, riferendosi alla parte di scatola che si vede nella figura del passaggio 11 (il lato opposto seguirà istruzioni analoghe), relativamente al quadrato bianco: piegare a valle il lato verticale e a monte la diagonale segnata, intascando il triangolo che si forma sotto a quello colorato.
- Ecco la scatola conclusa! La scatola è un parallelepipedo a base rettangolare, con due facce laterali quadrate e due rettangolari.
Per l’attività matematica potete chiamare $a$ il lato corto e $b$ il lato lungo del rettangolo di partenza. Potete proporre, dopo ogni passaggio di piegatura, di descrivere il poligono che compare e calcolarne perimetro e area, in funzione di $a$ e $b$.
Se la classe non fosse ancora abituata al formalismo, potete approssimare le lunghezze dei lati attribuendo la lunghezza di $21$ cm al lato corto e di $30$ cm al lato lungo (in effetti per il lato lungo si tratta di $29,7$ cm, ma dovendo poi calcolarne alcune frazioni vi suggerisco di approssimare).
Per esempio, la figura rappresentata nel passaggio 3 è un rettangolo di base $a$ e altezza $\dfrac{b}{4}$, che ha quindi area $A=a\cdot \dfrac{b}{4}=157,5$ cm2 e perimetro $p=2\left( a+\dfrac{b}{4}\right)=57$ cm.
In Zona Matematica, nell’area dedicata agli origami, potete trovare una scheda da proporre alla classe e relative soluzioni.
Vai all’area “Origami” del I grado
Vai all’area “Origami” del II grado – I biennio
