
Il problema che propongo è adatto a essere svolto in collaborazione, sia nella modalità di lavoro a coppie oppure in quella a gruppi più ampi, a seconda di quanto riterrete più opportuno per il vostro gruppo classe. Come già ho evidenziato in altri articoli, ogni situazione-problema potrebbe essere un semplice esercizio in una classe già matura per affrontarla oppure costituire un momento di attività più complessa in un’altra classe… è dunque solo la vostra sensibilità e la vostra intuizione che vi potranno suggerire se e come proporre le questioni che descrivo, frutto di esperienze realmente effettuate in classi di scuola secondaria di primo o di secondo grado.
Il problema del rettangolo
Il testo che segue è stato elaborato come sviluppo di un momento didattico in cui l’insegnante di una classe prima di un istituto professionale, per prendere atto della situazione cognitiva dei suoi alunni circa la rappresentazione di frazioni attraverso semplici figure geometriche, aveva chiesto a ognuno di colorare $\frac{1}{3}$ di un rettangolo in almeno due modi differenti. Oltre alle soluzioni più ovvie (la suddivisione in tre parti del rettangolo, disegnato in posizione canonica, attraverso due opportuni segmenti verticali o orizzontali) era stata proposta una soluzione un po’ diversa, che ha suscitato molto interesse e che è diventata poi oggetto di lavoro a gruppi, nella formulazione che segue:
L’insegnante ha chiesto di disegnare un rettangolo e di colorarne $\frac{1}{3}$. Irene ha suddiviso il suo rettangolo come vedete in figura (ha scelto di utilizzare il centro del rettangolo) e sostiene che la parte colorata sia esattamente $\frac{1}{3}$.

Giulia, la sua compagna di banco, dice che la parte ombreggiata non è $\frac{1}{3}$ del rettangolo e sostiene inoltre che non sia assolutamente possibile ottenere $\frac{1}{3}$ del rettangolo suddividendolo in quel modo.
Secondo voi, chi ha ragione? Spiegate bene la vostra risposta.
È evidente (anche a occhio) che le tre parti in cui è suddiviso il rettangolo non sono equivalenti, ma argomentare la scorrettezza della soluzione proposta non è immediato, perché richiede anzitutto una scelta di strategia (per esempio geometrica o algebrica) ed è noto come in questi casi, in cui non sono assegnati dati, non sia affatto scontato che gli alunni prendano l’iniziativa di dare nomi a punti o a misure. Pensando di suddividere il rettangolo in $8$ triangoli rettangoli congruenti (ciascuno di base e altezza la metà, rispettivamente, di base e altezza del rettangolo assegnato), il triangolo isoscele risulterebbe costituito da $2$ di questi triangoli, mentre le altre due parti, (i due trapezi rettangoli) sarebbero costituite, ciascuna, da $3$ di questi triangoli.
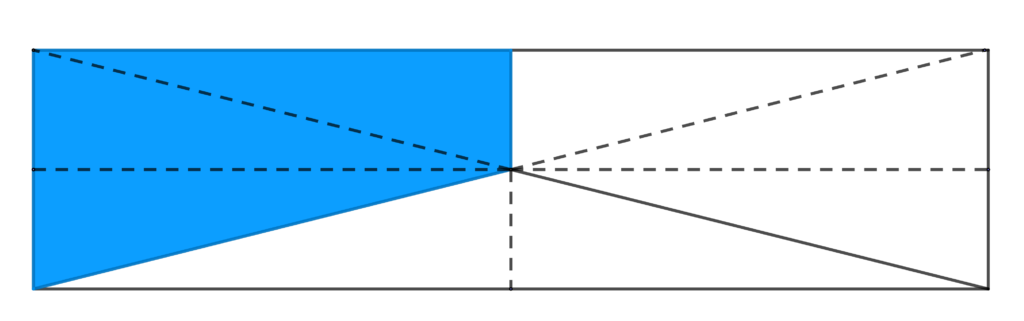
Dunque, la suddivisione proposta da Irene non è corretta. Notiamo che fino a questo punto la situazione potrebbe essere facilmente dominata anche a fine scuola primaria, quando si fanno numerose esperienze di equiscomponibilità.
Intraprendere una via algebrica potrebbe essere più complesso, perché se per esempio si chiamano rispettivamente $x$ e $y$ base e altezza del rettangolo assegnato, le tre parti in cui è suddiviso il rettangolo hanno area, rispettivamente, $\frac{xy}{4}$il triangolo isoscele e $\frac{3xy}{8}$ ciascuno dei due trapezi: anche ora è evidente che le parti non hanno la stessa area ma questa strada, a differenza della via geometrica, è più adatta agli alunni di scuola secondaria.
Lo sviluppo successivo, effettivamente realizzato in classe per rispondere all’obiezione di Giulia, forse adatto anche a una classe terza di secondaria di primo grado e certamente proponibile in una prima di secondo grado, è il seguente:
… Ma una suddivisione del tipo di quella proposta da Irene, non potrebbe proprio rispondere al nostro problema di suddivisione del rettangolo in tre parti di ugual area?
Questa volta la via algebrica sembra più naturale: indicando ancora con $x$ e $y$, rispettivamente, base e altezza del rettangolo assegnato e con $z$ l’altezza del triangolo isoscele, si vuole che l’area del triangolo isoscele sia $\frac{1}{3}$ di quella del rettangolo, cioè
$\frac{xz}{2}=\frac{xy}{3}$
Dunque la soluzione esiste, deve essere $z=\frac{2}{3}y$. Si tratta dunque di una soluzione espressa in generale, che potrebbe anche essere verificata in alcuni casi numerici semplici. Osserviamo che impostare l’uguaglianza tra l’area del triangolo isoscele e quella del trapezio sarebbe solo più complesso: se si impone che l’area del triangolo isoscele sia $\frac{1}{3}$ dell’area del rettangolo, le altre due parti, cioè i due trapezi, che sono fra loro congruenti, saranno necessariamente anch’essi $\frac{1}{3}$ ciascuno!
