Pensiero computazionale e le probabilità del gioco del Sinco

Siamo ormai nel $2025$, quasi all’inizio del secondo quarto del nuovo millennio. L’importanza delle discipline STEM cresce di anno in anno e forse per renderle alla portata di studentesse e studenti potrebbe essere opportuno facilitare in ragazze e ragazze lo sviluppo di un pensiero flessibile e computazionale. Il pensiero computazionale sembra essere centrale anche per migliorare il livello di accuratezza, di qualità delle domande poste e la capacità di valutare dati, informazioni e strategie risolutive offerte dall’AI, in modo che studentesse e studenti riescano a effettuare il miglior utilizzo umano dell’AI. Il pensiero computazionale, inoltre, aiuta a concentrare l’attenzione più sui processi che sui prodotti.

Di seguito vi propongo un esempio che prende spunto dal calcolo della probabilità di vincita del gioco del Sinco per provare a impostare in modo computazionale la strategia relativa. Questo gioco di Tombola napoletana offre delle possibilità diverse dalla semplice estrazione da un mazzo di carte napoletane.

Il gioco del Sinco è una variante della Tombola che usa le carte napoletane invece dei numeri tradizionali. Le vincite possibili sono:

• ROMBO: coprire le quattro carte nel rombo centrale
• ANGOLO: coprire le quattro carte agli angoli
• POKER: coprire le quattro carte dello stesso valore in alto a sinistra  
• SINCO: coprire cinque carte che formano una linea (orizzontale superiore/inferiore, verticale sinistra/destra o diagonale principale/secondaria)

Rombo, angolo e poker hanno le stesse possibilità di formarsi, così come le sei linee del sinco.

In particolare, se si estraggono $5$ carte consecutivamente:

• $p($estrarre la prima carta specifica da $40$ carte$) =\dfrac{5}{40}$
  
• $p($estrarre la seconda carta specifica dalle rimanenti $39$ carte$) =\dfrac{4}{39}$
  
• $p($estrarre la terza carta specifica dalle rimanenti $38$ carte$) =\dfrac{3}{38}$
  
• $p($estrarre la quarta carta specifica dalle rimanenti $37$ carte$) =\dfrac{2}{37}$
  
• $p($estrarre la quinta carta specifica dalle rimanenti $36$ carte$) =\dfrac{1}{36}$

$p(5$ carte specifiche$) =\dfrac{5}{40}\cdot \dfrac{4}{39}\cdot \dfrac{3}{38}\cdot \dfrac{2}{37}\cdot \dfrac{1}{36}$ estraendo $5$ carte

Se invece si estraggono un certo numero di carte $n$ maggiore di $5$ la probabilità di fare poker o estrarre $5$ carte specifiche si può calcolare mediante la distribuzione ipergeometrica:

per $k$ successi in $n$ estrazioni da $N$ ($40$) carte: $p\left( n,k\right) =\dfrac{C\left( k,k\right) \cdot C\left( N-k,n-k\right) }{C\left( N,n\right) }$

Per esempio per il poker ($4$ successi) in $20$ estrazioni da $40$ carte:

$p($poker$) =\dfrac{C\left( 4,4\right) \cdot C\left( 40-4,20-4\right) }{C\left( 40,20\right) }\approx 0,3075=30,75\%$

Per le $5$ carte specifiche ($5$ successi) in $20$ estrazioni da $40$ carte:

$p(5$ carte specifiche$) =\dfrac{C\left( 5,45\right) \cdot C\left( 40-5,20-5\right) }{C\left( 40,20\right) }\approx 0,2756=27,56\%$

Nel gioco del Sinco poker, angolo e rombo hanno le stesse probabilità, quindi la possibilità di fare uno dei tre è data dalla somma delle probabilità singole, tre volte quella del poker.
Anche tutte le $6$ linee hanno la stessa singola probabilità di essere coperte. 
Per il Sinco quindi molte studentesse e studenti (e anche i chat bot di AI) affermano che la probabilità è data dalla somma delle probabilità delle singole linee, cioè $6$ volte la probabilità di una linea.
Esaminando con attenzione la tabella del gioco si può capire che non è così.

Mentre il poker e l’angolo hanno una sola carta in comune (la carta in un angolo superiore sinistro) e nessuna con il rombo, per come sono disposti nella tabella, le linee hanno varie carte in comune. Ogni carta corrispondente a un angolo serve a completare di coprire tre linee. La carta al centro serve a completare entrambe le diagonali.

Si potrebbe chiedere a studentesse e studenti se il fatto che una stessa carta agli angoli appartenga a tre linee incrementi o diminuisca la probabilità totale di coprire una delle linee.
Se la classe è ancora agli inizi dello studio del calcolo delle probabilità, è interessante sperimentare come il tipo di risposta sia sostanzialmente diverso a seconda di quali termini si utilizzino per porre la domanda: 

1. la stessa carta serve per completare tre linee. Questo fatto aumenta o diminuisce la probabilità di coprire una delle linee?
2. la stessa carta può essere utilizzata non solo in una linea ma in tre contemporaneamente. Questo fatto aumenta o diminuisce la probabilità di coprire una delle linee?

Nelle mie sperimentazioni nel secondo caso le risposte che affermano un aumento della probabilità sono maggiori che nel primo.
In realtà il calcolo delle probabilità del Sinco, calcolando anche solo le carte agli angoli (e non quella al centro) in comune fra le varie linee, è molto complesso, come mostra lo schema di seguito:

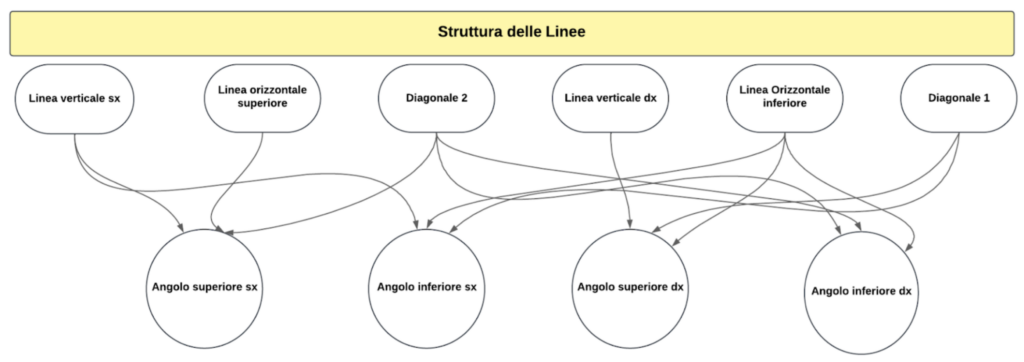
Per aiutare lo sviluppo di un pensiero computazionale, si può chiedere alla classe di provare a descrivere a grandi linee una strategia risolutiva del calcolo della probabilità di coprire una delle sei linee, di fare sinco, mediante un diagramma di flusso, chiarendo bene prima cosa si intenda per diagramma di flusso.

Un insieme di operazioni, istruzioni descritte a parole, non diventa automaticamente un diagramma di flusso se inserite singolarmente in box e collegate verticalmente tra loro. I diagrammi di flusso sono nati in ambito informatico per descrivere procedure che utilizzano strutture di controllo, necessitando durante il loro svolgimento di test (if, then, else) o cicli (repeat until, do for). Quindi studentesse e studenti si dovranno impegnare in una descrizione che contempli azione ripetute e test, per lo meno di completamento procedura.

Premettendo che:

• le dipendenze tra le linee (dovute agli angoli condivisi) rendono il calcolo molto più complesso di quanto sembri inizialmente
• è fondamentale considerare tutte le possibili configurazioni degli angoli estratti, poiché ogni configurazione offre diverse opportunità di completare una linea

suggerire di:

1. partire identificando le $16$ carte uniche che compongono le linee
2. suddividerle in angolari ($4$) e non angolari ($12$)
3. per ogni possibile combinazione di $k$ carte angolari estratte:

• calcolare quante carte non angolari servono per completare almeno una linea
• usare la distribuzione ipergeometrica per calcolare la probabilità di queste carte (condizionate all’estrazione della carta angolare) e moltiplicarla per la probabilità di estrarre la carta angolare (teorema di Bayes)

Di seguito vi riporto l’immagine del diagramma di flusso di un gruppo di studentesse e studenti di una classe quarta della scuola secondaria di secondo grado.

Ovviamente ai primi tentativi i diagrammi, anche considerandoli approssimati, presentano diversi errori. In questo caso studentesse e studenti hanno scritto correttamente di considerare tutte le combinazioni di estrarre $k$ carte angolari ma poi hanno calcolato solo un caso, mentre avrebbero dovuto rappresentare un ulteriore ciclo esterno, ma anche ragionare su questi errori aiuta a sviluppare un pensiero computazionale in studentesse e studenti e a migliorare il nostro lavoro di insegnanti.