
L’attività che vi propongo può essere usata a più livelli scolastici e in vari momenti dell’anno e parte dalla piegatura della base della girandola. La base della girandola è il punto di partenza di molti modelli origami e ha il pregio di essere un modello simpatico: può essere infatti anche attaccata a un bastoncino con una puntina e fatta girare nel vento.
L’esercizio matematico legato alla piegatura è quello di scomporre e ricomporre una figura geometrica complessa in figure semplici (come triangoli, quadrati e trapezi). A un livello più elementare si può chiedere agli alunni di individuare diverse scomposizioni della figura; a un livello più approfondito si può chiedere di calcolare l’area della figura utilizzando di volta in volta la formula di una sola figura elementare.
Ecco la sequenza di piegatura con le relative istruzioni; si parte da un foglio quadrato.

1. Portare un lato sul lato opposto, piegare e riaprire.
2. Portare i due lati paralleli alla piega fatta sulla piega stessa e riaprire. Il foglio resta suddiviso in 4 rettangoli congruenti.
3. e 4. Lavorando ora sull’altra coppia di lati paralleli, ripetere i passaggi 1 e 2.
5. Piegare le due diagonali e riaprire.
6. Voltare il foglio e portare tutti i vertici al centro. Riaprire.
7. Voltare nuovamente il foglio e portare i 4 punti medi dei lati al centro, sfruttando le pieghe precedenti. Nel passaggio 7 viene mostrato il movimento su uno di essi e il passaggio 8 mostra la posizione finale della carta, in 3D.
9. Appiattire ora la carta portando verso l’esterno i vertici del quadrato iniziale.
Ecco alcuni spunti che potete sviluppare in una lezione di matematica. Modificateli a vostro piacere, adattandoli al livello di conoscenza dei vostri alunni.
Esercizio 1
Ridisegna almeno tre volte sul quaderno la girandola, evidenziando la traccia lasciata dalle pieghe.
Tenendo conto delle linee dei bordi della figura e della traccia lasciata dalle pieghe, prova a scomporre la girandola:
- in triangoli tutti congruenti
- in triangoli simili
- in trapezi
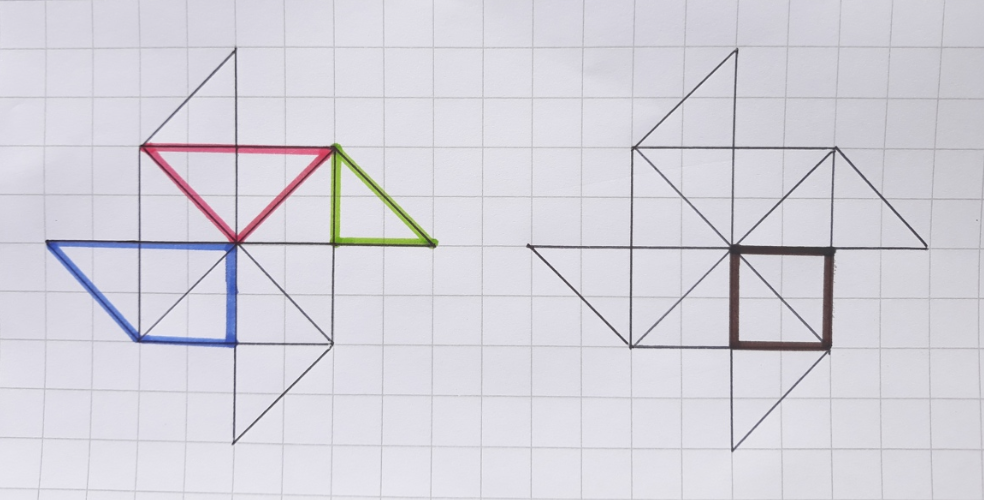
Traccia di soluzione
La Figura 2 mostra che la girandola si può scomporre in: 12 triangoli tutti congruenti a quello indicato in verde; 4 triangoli come quello rosa e 4 triangoli verdi che sono tutti simili tra loro ma non congruenti; 4 trapezi blu.
Esercizio 2
Possiamo vedere la girandola come unione di un quadrato centrale e di 4 triangolini esterni. Poniamo uguale a 2 la misura del lato del quadrato centrale. Scomponendo la figura ed eventualmente ricomponendo alcune sue parti, calcolane l’area seguendo queste indicazioni:
- usa solo la formula dell’area dei quadrati
- usa solo la formula dell’area dei triangoli
- usa solo la formula dell’area dei trapezi
Traccia di soluzione
La Figura 2(b) mostra un quadrato marrone che ha lato l lungo 1 cm rispetto alle ipotesi date; quindi l’area del quadrato marrone è l x l = 1 cm x 1 cm = 1 cm2. Per rispondere alla domanda 1 si può osservare che coppie di triangolini esterni (verdi nella 2(a)) compongono un quadrato congruente a quello marrone. Quindi l’area della girandola è equivalente a quella di 6 quadratini marroni, cioè è 6 cm2.
Volendo usare solo la formula dell’area dei triangoli (richiesta 2), osserviamo che ogni triangolino ha area
e la girandola è coperta da 12 triangolini; quindi ha area pari a 12 x 0,5 cm2 = 6 cm2.
Per la richiesta 3, rifacendoci alla Figura 2(a), notiamo che l’area della girandola è 4 volte l’area del trapezio blu. Quindi:
