
Perché non usare la piega della carta per sperimentare soluzioni di un problema di realtà? Ecco una proposta da sperimentare in classe.
IL PROBLEMA
La ditta ELOTACS produce fogli di alluminio rettangolari, come quello in figura; la base $AB$ è lunga $28$ cm e l’altezza $BC$ è lunga $18$ cm.

La ditta vuole utilizzare i fogli per realizzare delle scatole che conterranno formaggio grattugiato. Li vuole quindi piegare con rette parallele a $BC$ in modo da formare la superficie laterale del parallelepipedo. Userà poi dei tappi di plastica come basi e coperchi dei parallelepipedi.
Chiede allora a un ingegnere matematico di suggerire alcune soluzioni di scatola. Ecco le due proposte.
Proposta 1
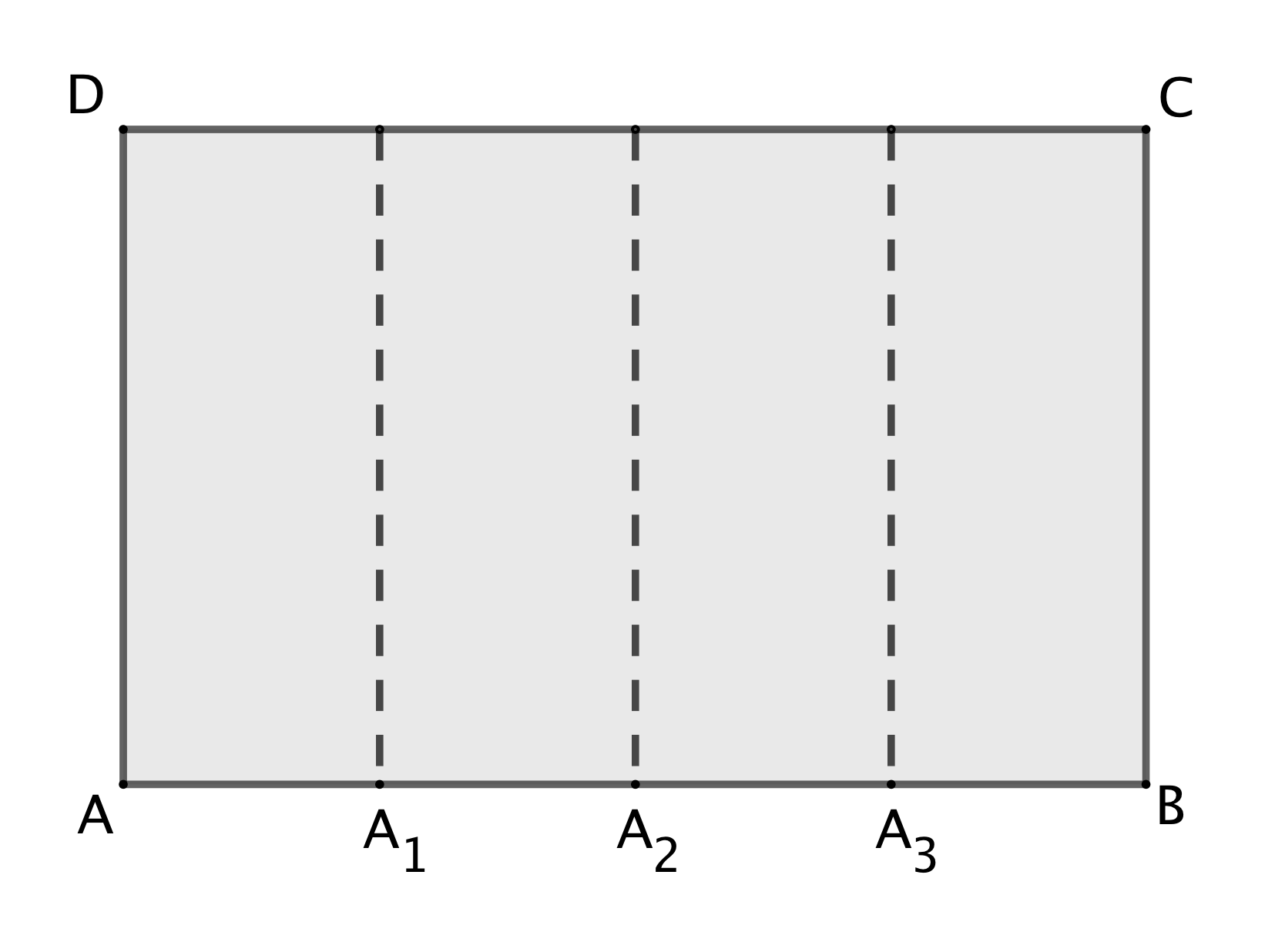
La base viene divisa in quattro segmenti congruenti $A{A_1} = {A_1}{A_2} = {A_2}{A_3} = {A_3}B = 7$ cm; viene poi piegato l’alluminio lungo segmenti paralleli a $BC$ e passanti rispettivamente per ${A_1}$, ${A_2}$, ${A_3}$. Infine si saldano i lati $BC$ e $AD$ per chiuderla.
Proposta 2
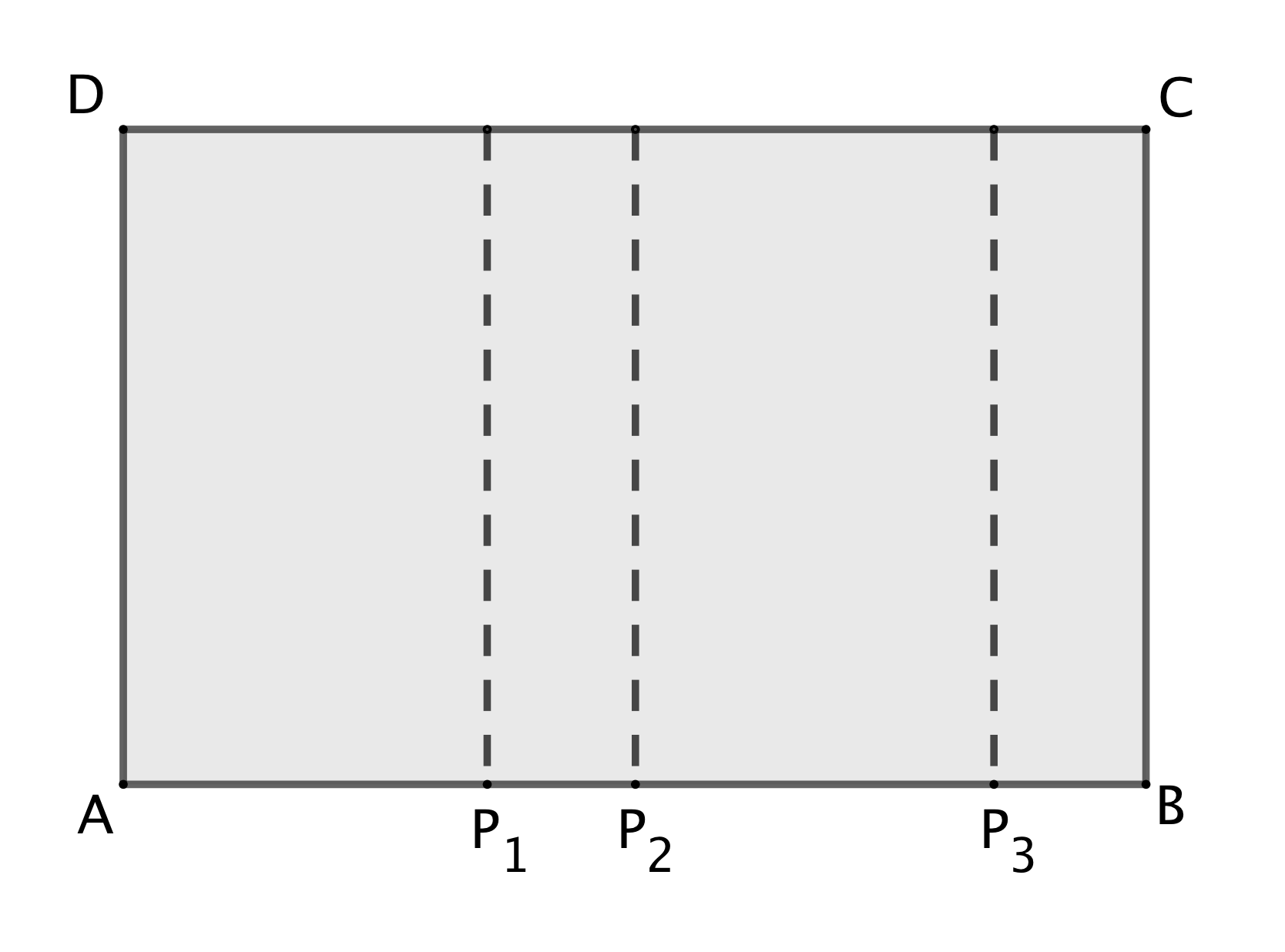
La base viene divisa in quattro segmenti a due a due congruenti: $A{P_1} = {P_2}{P_3} = 10$ cm, ${P_1} {P_2}= {P_3}B = 4$ cm. Come nel progetto precedente, l’alluminio viene poi piegato lungo segmenti paralleli a $BC$ e passanti rispettivamente per ${P_1}$, ${P_2}$, ${P_3}$. La scatola, a base rettangolare, viene saldata lungo i due segmenti esterni.
LE ATTIVITÀ
1. Realizzazione del prototipo
Distribuire dei fogli A4 con i quali gli studenti realizzeranno la superficie laterale delle scatole, seguendo le istruzioni proposte. Mostriamo le istruzioni per la scatola a base quadrata, che si adattano facilmente anche alla scatola a base rettangolare.
Le linee tratteggiate, poste circa a $1,5$ cm dai lati lunghi, vanno eseguite per prime e poi lasciate chiuse: servono come “tasche” per chiudere la scatola. Una volta eseguite resterà un rettangolo di dimensioni $29,2$ cm e $18$ cm (circa).
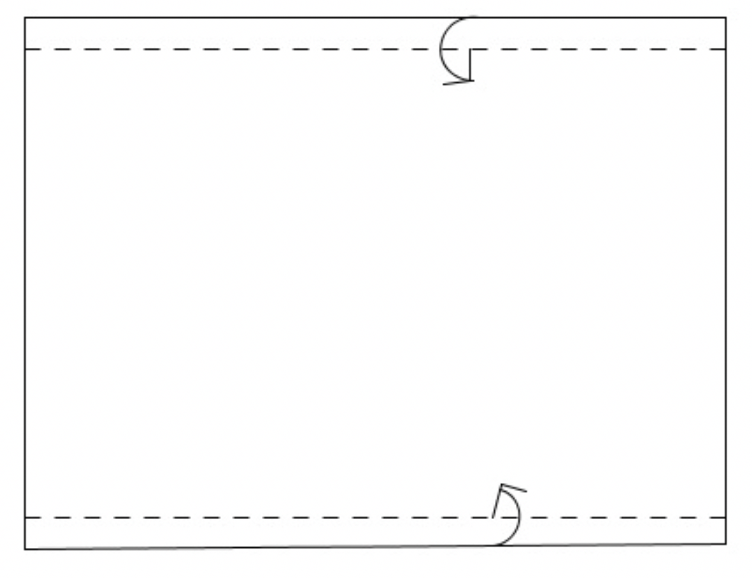
Piegare, lungo la linea tratteggiata, i lati lunghi del foglio verso l’interno.
Si ottiene un rettangolo di dimensioni $29,2$ cm e $18$ cm (circa).
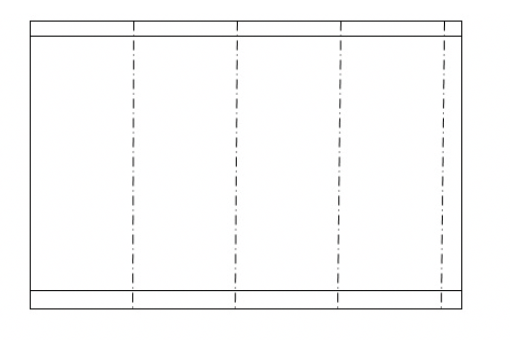
Piegare lungo le linee tratto-punto senza chiuderle completamente, dando al foglio la forma delle superficie laterale del parallelepipedo.
Intascare la striscia verticale rettangolare più piccola per chiudere la scatola.
Ecco la parete esterna della scatola.
Ricorda che poi la ditta metterà base e coperchio di plastica.
2. Scelta della proposta migliore
Nei due progetti vengono usati fogli di alluminio della stessa grandezza. In quale dei due casi la scatola conterrà più formaggio? Che scatola conviene produrre per non sprecare alluminio?
3. Nuove idee di progettazione
Sei in grado di realizzare una scatola a base esagonale partendo dallo stesso foglio di alluminio? Conterrà più formaggio delle precedenti?
Sapresti ipotizzare che forma deve avere la base della scatola perché, utilizzando lo stesso foglio di alluminio, essa contenga più formaggio possibile?
OSSERVAZIONI
Il problema proposto, anche se “mascherato” con un problema di volumi, è in effetti un problema isoperimetrico. Infatti l’altezza dei contenitori è fissa e ciò che farà variare il volume sarà l’area di base. Con semplici conti, dopo aver osservato le scatole, gli studenti potranno verificare che la base quadrata è più conveniente di quella rettangolare e che la base esagonale è più conveniente di quella quadrata. Gli studenti dovrebbero essere portati a pensare che la base che ottimizza meglio il nostro problema è quella circolare, utilizzata in effetti per molti tipi di lattine.
