
In molte occasioni potreste accorgervi che i vostri alunni tendono a non dare sufficiente attenzione al procedimento risolutivo di un problema, preoccupandosi soltanto che il risultato ottenuto sia esatto. Si tratta di un atteggiamento diffuso, nonostante i vostri sforzi per promuovere nei ragazzi consapevolezza e senso critico sulle procedure scelte; tuttavia possiamo condividere, in questo caso, una riflessione interessante: se gli alunni si comportano in questo modo forse significa che non siamo ancora riusciti a comunicare loro quanto invece sia importante riflettere a fondo sui procedimenti risolutivi messi in atto, confrontandoli per esempio con altri per poter arrivare a scegliere il più opportuno (perché più breve o perché più semplice o per altri motivi legati al gusto personale di ciascuno).
È evidente che l’azione di voi insegnanti risulta a questo punto decisiva, proprio perché può orientare l’attenzione dei ragazzi, di fronte a un problema da risolvere, a prendere in considerazione più procedure possibili: la via più semplice da adottare è proprio quella di richiedere esplicitamente, nel testo del problema, soluzioni differenti, su cui possano poi concentrarsi, in sede di confronto critico svolto in classe, le discussioni successive sulle varie proposte. Affinché la riflessione sulle procedure diventi un’abitudine è indispensabile riuscire a proporla con una certa continuità, così che pian piano possiate vederla consolidarsi, diventando un atteggiamento proprio di ogni alunno.
L’attività svolta in collaborazione (fra pari o in gruppi più ampi) può certamente promuovere la varietà di soluzioni, soprattutto se prima che ciascuno comunichi le proprie idee al compagno o ai compagni del gruppo viene osservato, come è auspicabile, qualche momento di riflessione personale in silenzio, così che ognuno possa poi dar spazio alle proprie strategie senza essere troppo influenzato dalle idee del compagno o dei compagni di gruppo.
Ecco un problema1 che potrebbe essere proposto a questo scopo, per esempio in una classe prima o successiva, se volete avviare o potenziare l’abitudine alla riflessione sulle procedure:
Una questione di aree…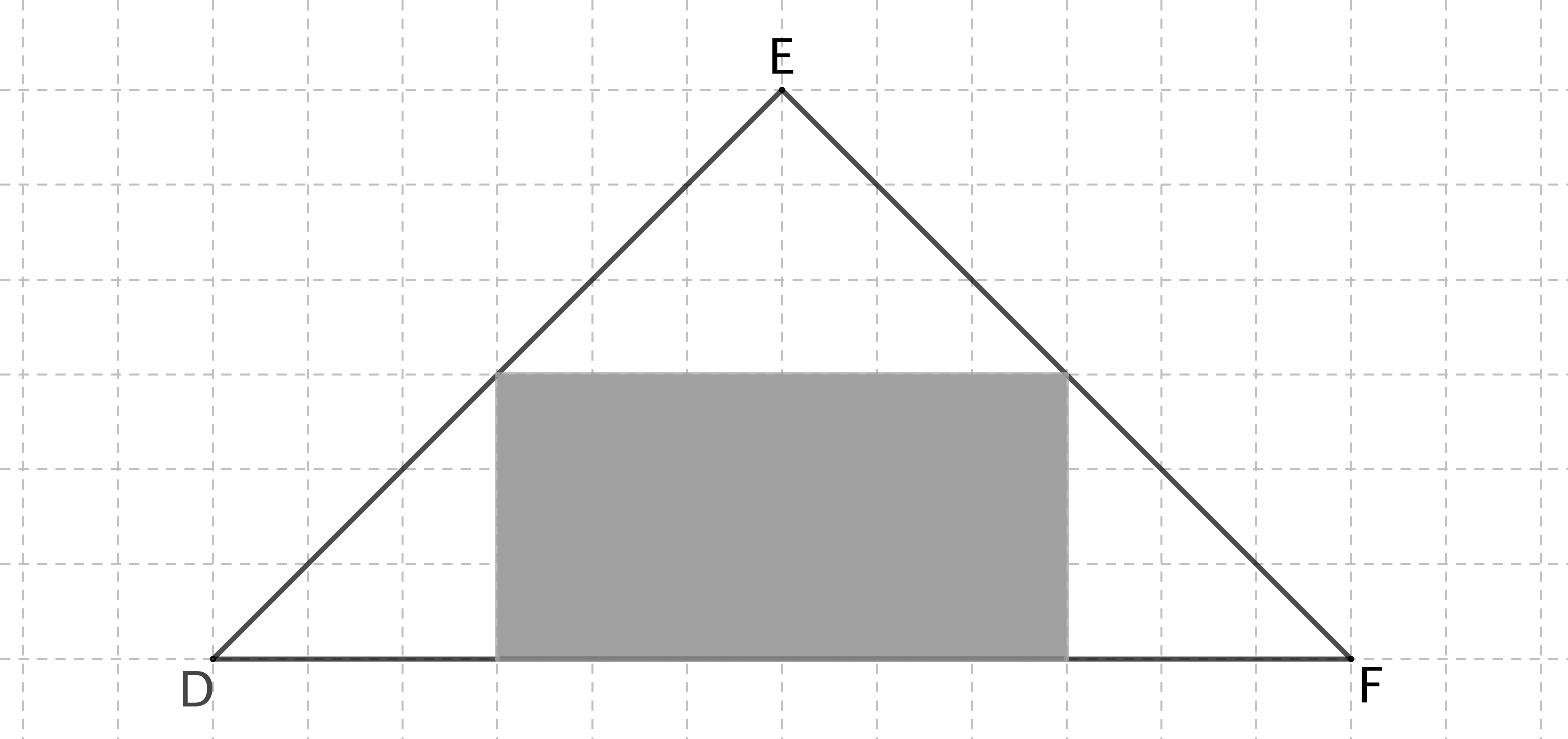
Osserva la figura. A quale frazione dell’area del triangolo $DFE$ corrisponde il rettangolo grigio?
Individua almeno due modi diversi per risolvere il problema e giustifica i tuoi procedimenti.
Il problema, molto semplice, affronta una questione di calcolo di aree ma al contrario degli usuali compiti di geometria non presenta alcun dato numerico. Come sapete, questo può costituire un primo ostacolo, specie se è molto radicata nei ragazzi l’abitudine di associare la soluzione di un problema al dover svolgere calcoli: proprio per questo risulta interessante la domanda, che richiede subito di escogitare una strategia, nel nostro caso in base alla quadrettatura della griglia proposta nella figura. Si può comunque procedere in modo diverso, per esempio ricorrendo a formule conosciute oppure procedendo in modo più sintetico, cioè scomponendo la figura e osservando le relazioni fra le varie parti, come descrivo di seguito.
Come accennato, ricorrendo alla quadrettatura si può calcolare l’area del rettangolo grigio: $A_{R}=b\times h=6\times 3=18$ quadretti e analogamente si può calcolare l’area del triangolo $DFE$: $A_{T}=\dfrac{b\times h}{2}=\dfrac{12\times 6}{2}=36$ quadretti. Facendo il rapporto fra la prima e la seconda area si ottiene $\dfrac{18}{36}$, cioè $\dfrac{1}{2}$.
È anche possibile associare direttamente a ogni quadretto la misura unitaria del lato e dunque arrivare a riproporre lo stesso rapporto: è interessante infatti notare che non è importante precisare se si tratti di quadretti o di cm2, perché il rapporto non dipende dall’unità di misura scelta. Questa osservazione non è banale ma può essere proposta se pensate che i vostri alunni siano pronti a comprenderla.
In altro modo si può vedere la figura scomposta in triangoli rettangoli congruenti, come quelli ai lati del rettangolo grigio, ciascuno con cateti di $3$ quadretti. Il rettangolo ne comprende $4$, mentre il triangolo $DFE$ $8$ (vanno contati ovviamente anche quelli della parte grigia, un errore potrebbe essere infatti quello di contare solo quelli della parte bianca); il rapporto richiesto è, dunque, $\dfrac{4}{8}$, cioè $\dfrac{1}{2}$.
Un altro modo di procedere potrebbe essere quello di osservare l’equivalenza fra l’area della parte bianca e l’area della parte grigia di $DFE$, ancora basandosi sul calcolo di tali aree o sulla scomposizione in triangoli rettangoli o sul trasporto di figure (per esempio ruotando i tre triangoli bianchi sui lati del rettangolo grigio in modo che $F$ e $D$ coincidano con il vertice $E$, andando a costruire un rettangolo bianco esattamente sul grigio e dunque insieme equivalenti alla parte grigia).
Di conseguenza il triangolo $DFE$ risulta suddiviso in due parti equivalenti e quella grigia è metà del totale, cioè ancora il rapporto richiesto è $\dfrac{1}{2}$.
Confrontando i risultati ottenuti, a seconda del procedimento attuato, si hanno come soluzioni frazioni diverse, come per esempio nel nostro caso $\dfrac{18}{36}$, $\dfrac{4}{8}$, $\dfrac{1}{2}$, ovviamente equivalenti. Questa potrebbe essere dunque un’occasione per riprendere il significato e l’individuazione di frazioni equivalenti, qualora fosse utile riprendere questo elementare aspetto aritmetico delle frazioni.
Il problema proposto mi sembra dunque un’occasione interessante per condividere e confrontarsi su strategie diverse di soluzione, soprattutto in ambito collaborativo; la creatività e l’intuizione di ogni singolo studente potrebbe far emergere singolari e ulteriori motivazioni in aggiunta a quelle descritte. È evidente che il risultato richiesto è molto semplice, tuttavia proprio questa semplicità potrebbe favorire l’incremento dell’attenzione dei vostri alunni nell’escogitare strade differenti, sviluppando in loro un certo gusto nella scoperta di soluzioni alternative, esattamente nella direzione di focalizzarli maggiormente sulle procedure piuttosto che sui risultati.
1 Tratto dal quesito 11 del Fascicolo 1 delle Prove INVALSI a.s. 2015-2016, Prova di Matematica per la Classe Quinta della Scuola primaria. Qui il quesito è stato modificato, togliendo le risposte multiple originali e aggiungendo la richiesta di due strategie, così da evidenziare la molteplicità delle possibili soluzioni e dando spazio ad opportune argomentazioni per motivare le scelte.
