
Vediamo oggi come possiamo applicare alcuni concetti probabilistici a un gioco da tavolo molto diffuso: il Monopoly. L’argomento può essere utilizzato per una lezione frontale ma anche per una semplice attività laboratoriale, da svolgere a distanza.
Per chi non conoscesse il gioco le regole sono queste:
- ogni giocatore si muove sulle caselle del tabellone tirando due dadi;
- quando un giocatore arriva su una casella che non è di proprietà di un altro può comprarla e costruire in quel terreno delle case;
- quando un giocatore arriva su una casella che è di proprietà di un altro deve pagare al proprietario una cifra che dipende da dove si trova il terreno (ci sono vie più economiche e altre più care) e dal numero di case che sono presenti (più case sono presenti più si paga);
- un giocatore che finisce il denaro viene eliminato;
- quando rimane solo un giocatore la partita termina e questo giocatore ha vinto.
Ci sono molte altre regole e casistiche, ma queste sono sufficienti per capire i ragionamenti che faremo.
Per muoversi nel tabellone si usano due dadi da $6$ ed è chiaro che si può avanzare di un numero di passi che va da un minimo di $2$ ($1+1$) a un massimo di $12$ ($6+6$).
La cosa interessante è che non tutti i numeri tra $2$ e $12$ hanno la stessa probabilità di verificarsi.
Vediamo con una tabella quali sono le possibili combinazioni risultanti dal lancio di due dadi (le caselle centrali della tabella contengono la somma dei due valori di ciascun dado).
| + | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ |
| $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ |
| $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ |
| $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ |
| $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ |
| $5$ | $6$ | $7$ | $8$ | $9$ | $10$ | $11$ |
| $6$ | $7$ | $8$ | $9$ | $10$ | $11$ | $12$ |
Un totale di $3$ si può ottenere solamente in due modi: come $1+2$ o come $2+1$. Un totale di $7$ si può ottenere invece in $6$ modi diversi: $1+6$, $2+5$, $3+4$, $4+3$, $5+2$, $6+1$.
Per trovare le probabilità di fare un certo numero di passi dobbiamo dividere il numero di modi in cui si può ottenere quel numero per tutti i casi possibili, che sono $36$.
Nella tabella vengono mostrate le probabilità di spostarsi di un certo numero di passi.
| $P\left( n \right)$: probabilità di avanzare di $n$ passi |
| $P\left(2 \right)=2,8$% |
| $P\left( 3 \right)=5,6$% |
| $P\left( 4 \right)=8,3$% |
| $P\left( 5 \right)=11,1$% |
| $P\left( 6 \right)=13,9$% |
| $P\left( 7 \right)=16,7$% |
| $P\left( 8 \right)=13,9$% |
| $P\left( 9 \right)=11,1$% |
| $P\left( 10 \right)=8,3$% |
| $P\left( 11 \right)=5,6$% |
| $P\left( 12 \right)=2,8$% |
Vediamo che il valore che si ottiene con maggiore probabilità è il $7$ e gli altri hanno probabilità simmetriche che decrescono allontanandosi dal valore centrale.
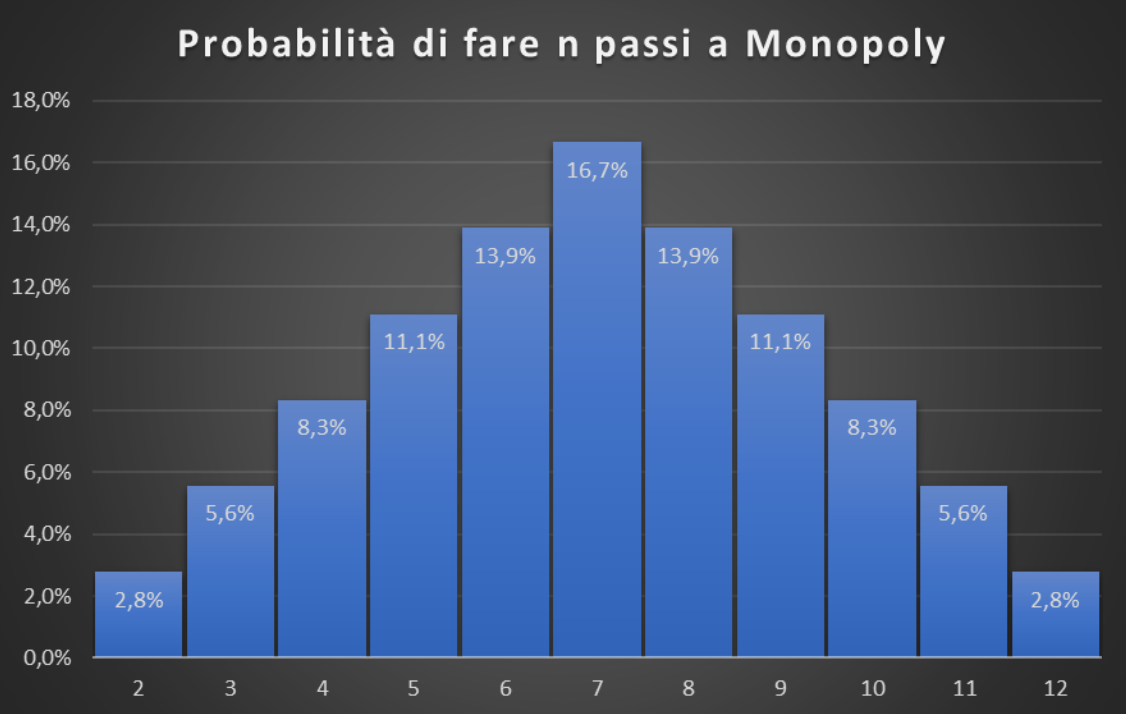
La probabilità di ottenere un $7$ è sei volte più grande di quella di ottenere un $2$ o un $12$. Un’altra cosa interessante è che la probabilità di ottenere uno dei tre numeri centrali $6$, $7$ o $8$ è del $44,5$%.
Sapere che il risultato del lancio di due dadi ha queste caratteristiche può dare un vantaggio strategico in una partita di Monopoly.
Immaginiamo che il nostro avversario si trovi in Corso Raffaello (una delle caselle arancioni) e che noi possediamo le tre vie rosse successive.
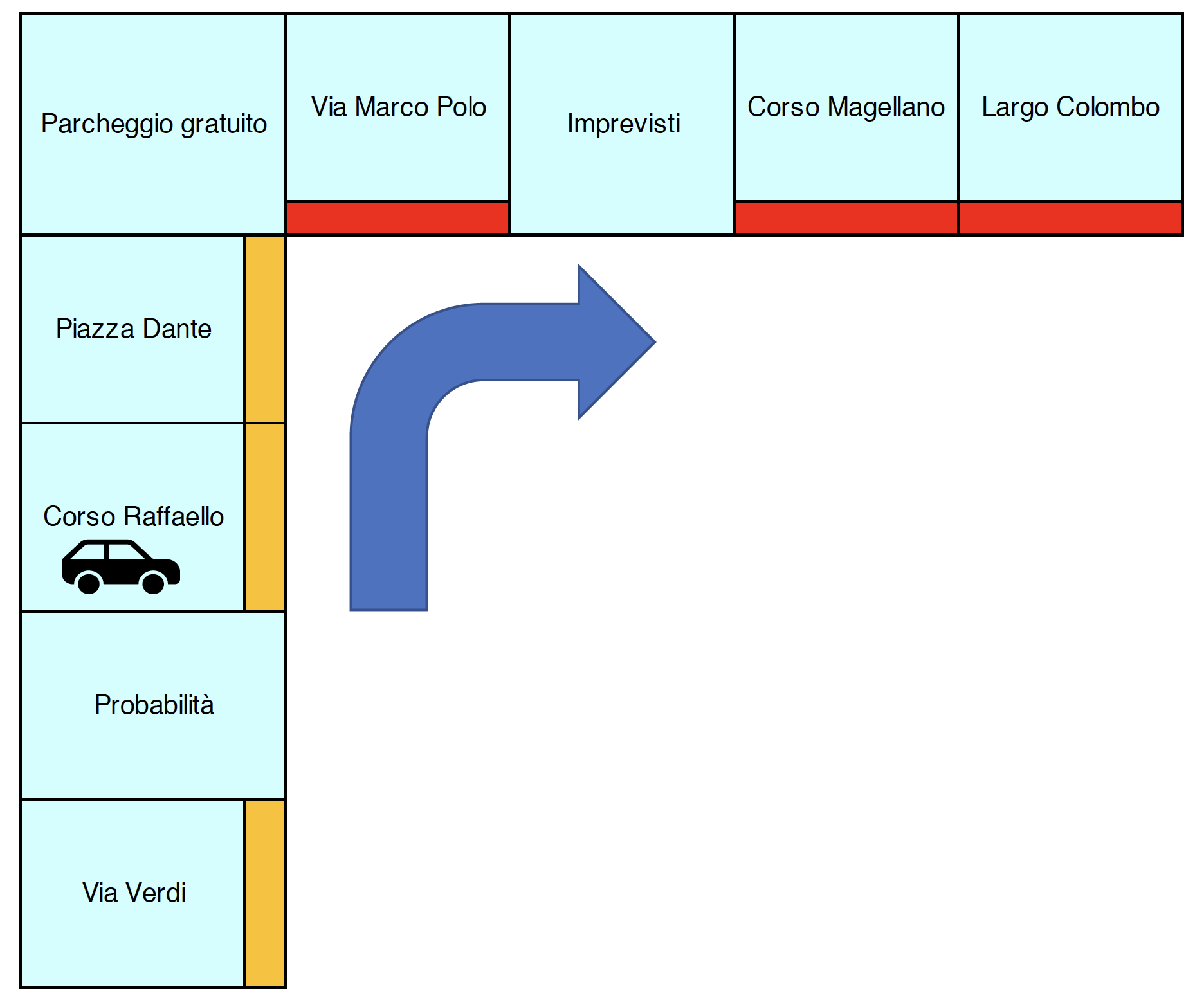
Vogliamo costruire una casa per cercare di far pagare all’avversario un prezzo maggiore nel caso arrivasse sulle nostre caselle ma abbiamo pochi soldi e ce ne possiamo permettere una sola. Dove ci conviene costruire la casa?
Le tre possibilità sono Via Marco Polo, Corso Magellano e Largo Colombo, che il nostro avversario potrebbe raggiungere rispettivamente in $3$, $5$ o $6$ passi.
Ma allora ci conviene costruire la casa su Largo Colombo perché tra le caselle rosse è quella che ha più probabilità di essere raggiunta dal nostro avversario nel prossimo turno!
Se avessimo abbastanza soldi per comprare due case allora potremmo decidere di costruire anche su Corso Magellano. La probabilità di fare $5$ oppure $6$ passi è del 25%, niente male!
Una parte importante della strategia del Monopoly è decidere qual è il momento giusto per investire dei soldi cercando di non fallire. Sapere quali sono le caselle che il nostro avversario raggiungerà con maggiore probabilità ci fornisce un criterio per poter prendere la decisione giusta al momento giusto. Poi, come in tutti i giochi che contengono una componente casuale come il lancio dei dadi o l’estrazione di carte da un mazzo, fare la scelta giusta non si traduce automaticamente in una vittoria, ma nell’avere una maggiore probabilità di vittoria.
Attività laboratoriale
Questo foglio di calcolo può essere usato per analizzare dal punto di vista statistico il risultato del lancio di due dadi. Il file è stato costruito pensando di far contribuire ciascuno studente della classe con $10$ realizzazioni del lancio di $2$ dadi per poi visualizzare la distribuzione campionaria di tutti i lanci.
Il file va preparato cancellando le realizzazioni inserite come esempio e compilando l’elenco con i nomi degli studenti. Fatte queste operazioni preliminari si può procedere allora in questo modo:
1) condividere il file con gli studenti utilizzando una qualsiasi piattaforma di condivisione;
2) chiedere a ciascuno studente di effettuare $10$ lanci con due dadi e di scrivere i $10$ risultati ottenuti nel file condiviso nella riga che corrisponde al suo nome;
3) mostrare agli studenti la distribuzione campionaria ottenuta e far vedere che i valori centrali sono stati ottenuti con una frequenza maggiore e, nel caso, fare altre considerazioni sul fatto che aumentando il campione esaminato la distribuzione convergerà a quella teorica.
