
In questo articolo voglio proporvi l’uso dell’origami per rendere meno astratti i polinomi. Come vedrete nel seguito ho scelto un semplice modello di casetta. La scelta è stata fatta per due motivi: la semplicità del modello, che lo rende particolarmente adatto a una piegatura “a distanza”, e il fatto che si possa partire sia da carta rettangolare, che porta a polinomi in due variabili, sia da carta quadrata, che permette di lavorare in una sola variabile.
Ovviamente potrete poi ripetere l’attività con altri modelli o cercarne da subito uno che sia più adatto alla vostra classe.
La proposta si articola in tre passaggii:
- costruiremo un paio di polinomi che “escono” naturalmente dalle pieghe origami del modello;
- utilizzeremo i polinomi per prevedere le misure finali di casette piegate da fogli di vari formati, andando a sostituire valori numerici nelle incognite;
- abbineremo ai polinomi le equazioni associate per risalire alle misure della carta da utilizzare per ottenere il modello nel formato desiderato.
Potete piegare in diretta con gli studenti il modello e poi lasciare che rispondano in autonomia alle domande, oppure prevedere una discussione allargata per coinvolgere la classe online.
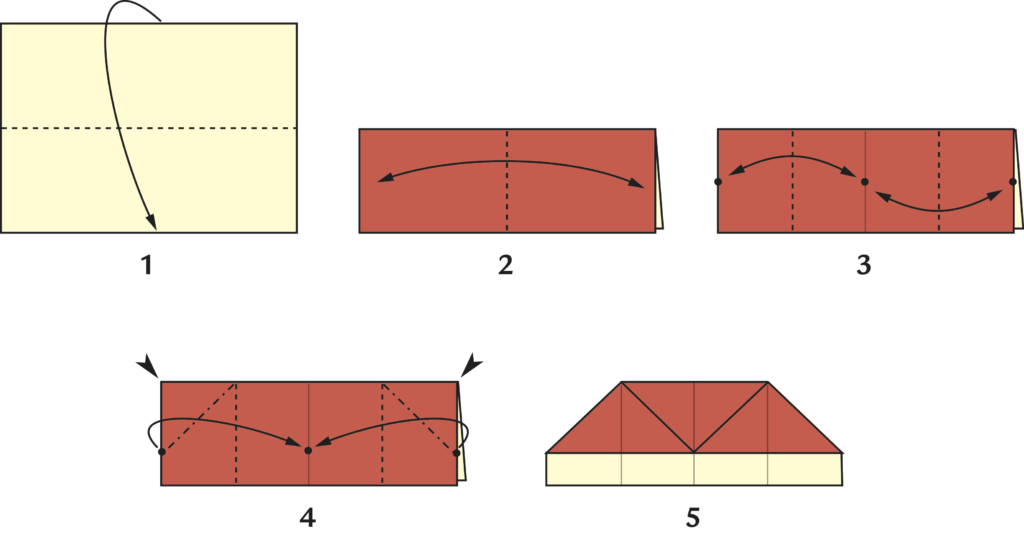
Il diagramma di piegatura che segue parte dal caso di foglio rettangolare, ma è facilmente adattabile al quadrato. Per iniziare, chiediamo ai ragazzi di partire da un foglio A4, facilmente reperibile.
L’unica istruzione da commentare è quella illustrata nel punto 4.
Appoggiamo il modello sul tavolo. Il modello è suddiviso in quattro rettangoli; consideriamo il più esterno a destra. Solleviamolo dal tavolo, portandolo perpendicolarmente al tavolo stesso (il resto della carta resta invece appoggiato). Inseriamo l’indice della mano destra tra i due strati di carta. Facciamo scorrere il dito sulla piega (sul lato lungo del rettangolo), verso l’alto, aprendo i due strati. Arrivati a fine corsa, schiacciamo il triangolo che si forma (e che sarà poi il tetto destro) portando quindi il lato corto sul lato lungo del rettangolo. Ripetiamo l’operazione con il rettangolo più esterno a sinistra.
Durante la piegatura, discutiamo con gli studenti sulle relazioni che devono intercorrere tra le misure dei lati del rettangolo di partenza, perché il modello possa essere piegato.
Questa discussione è molto interessante perché necessaria per ottenere “realmente” il modello. Il diagramma rappresenta la situazione di piegatura con carta bicolore. Gli studenti possono piegare un foglio bianco e colorare successivamente per meglio distinguere tetto e muro.
Riferendoci al foglio di partenza, poniamo $x$ il lato corto e $y$ quello lungo; matematicamente ciò si esprimerà con la relazione $x \le y$.
Facciamo osservare agli studenti che, nel passaggio 4., $\frac{1}{4}$ del lato lungo si deve poter schiacciare sulla verticale, lasciando lo spazio per il muro. Dovrà quindi essere $\frac{x}{2} > \frac{y}{4}$, cioè $x > \frac{y}{2}$.
In definitiva, avremo le seguenti limitazioni: $\frac{y}{2} < x \le y$.
Riprendendo quanto scritto all’inizio, le attività che possiamo ora proporre sono:
- Scrivere l’espressione che fornisce l’area del tetto (parte rossa in figura) e del muro (parte giallo chiaro in figura), in funzione delle misure $x$ e $y$ dei lati della carta di partenza.
(Risposta: ${A_{{\rm{tetto}}}} = \frac{3}{{16}}{y^2}$, ${A_{{\rm{muro}}}} = \frac{{xy}}{2} – \frac{{{y^2}}}{4}$). - Calcolare l’area del tetto e del muro se partissimo da fogli le cui dimensioni sono rispettivamente $21$ cm e $29$ cm, $21$ cm e $21$ cm. Nel secondo caso, dopo aver calcolato l’area, sostituendo nel polinomio, verificare il conto andando a piegare una casetta a partire da un quadrato di lato $21$ cm (i ragazzi potranno ottenerlo facilmente da un foglio A4).
- Se volessimo ottenere una casetta con tetto di $300{\rm{ c}}{{\rm{m}}^2}$, da che fogli dovremmo partire? Se invece volessimo una casetta con tetto $300{\rm{ c}}{{\rm{m}}^2}$ e muri di $200{\rm{ c}}{{\rm{m}}^2}$?
Gli studenti dovrebbero accorgersi che le misure del tetto dipendono solo dalla lunghezza $y$ del foglio e quindi la condizione sulla sola area del tetto non ci fornisce una soluzione unica di foglio.
Se invece, come nella seconda richiesta, vincoliamo anche la misura dell’area del muro, allora la soluzione (se esiste) è unica.
Osservazioni
- Si può ripetere l’attività, poggiando in orizzontale il lato corto del foglio di partenza (in questo caso la discussione è meno interessante).
- Se volete inizialmente avere polinomi in una sola variabile, potete partire direttamente dalla carta quadrata. Il passaggio a quella rettangolare mostrerà praticamente come a volte sia necessario utilizzare più di una variabile.
