
Quando si affronta lo studio della geometria dello spazio ci si scontra subito con problemi di visualizzazione degli oggetti. Molte volte cerchiamo di rappresentare rette, piani e superfici mediante disegni che ovviamente risentono della loro natura bidimensionale. Usando software di matematica dinamica, come GeoGebra, la visualizzazione sicuramente migliora proprio per la possibilità di muovere gli oggetti, ruotandoli o modificandone la posizione reciproca. La cosa migliore sarebbe però avere a disposizione dei modelli tridimensionali.
Iniziamo allora a costruire il punto di partenza di molte riflessioni di geometria analitica nello spazio: un sistema di riferimento ortogonale monometrico destrorso.
La costruzione parte da un semplice foglio di carta a quadretti (basta metà foglio protocollo o un foglio di un vecchio quaderno). Otterremo con poche pieghe un sistema di riferimento che può essere facilmente montato all’occorrenza e smontato per essere trasportato in un libro.
Il video mostra i passaggi di costruzione. La semplicità della costruzione e il materiale facilmente reperibile rende adatta la piegatura del modello anche in Didattica a Distanza.
Osservate che l’aletta che chiude il modello si riapre facilmente e permette quindi di trasportare il modello in un libro o in un quaderno.
Una volta che i vostri studenti avranno a loro disposizione il triedro, potete osservarlo insieme, focalizzando l’attenzione su questi passaggi.
- Colorate internamente gli spigoli che rappresentano gli assi $x$, $y$ e $z$, orientandoli opportunamente.
Usate questa attività per riprendere il concetto di terna destrorsa (usata anche in Fisica, nel prodotto vettoriale). Osservate anche che le tre rette si intersecano in un punto comune: l’origine.
- Fissate le unità di misura.
Anche qui potete discutere sull’opportunità di un sistema monometrico.
- Potete ora descrivere, prima sinteticamente poi analiticamente, i piani che contengono a coppie gli assi.
Per arrivare in modo naturale alle equazioni, scelto un piano potete far disegnare qualche punto di esso, trovandone le coordinate.
Osservate con i ragazzi che due di questi piani si intersecano in una retta e tutti e tre si intersecano in un punto: l’origine.
Potete ora fare semplici domande sulla posizione reciproca di rette e piani. Gli studenti baseranno le loro risposte sull’osservazione attiva del loro triedro. Ecco qualche domanda:
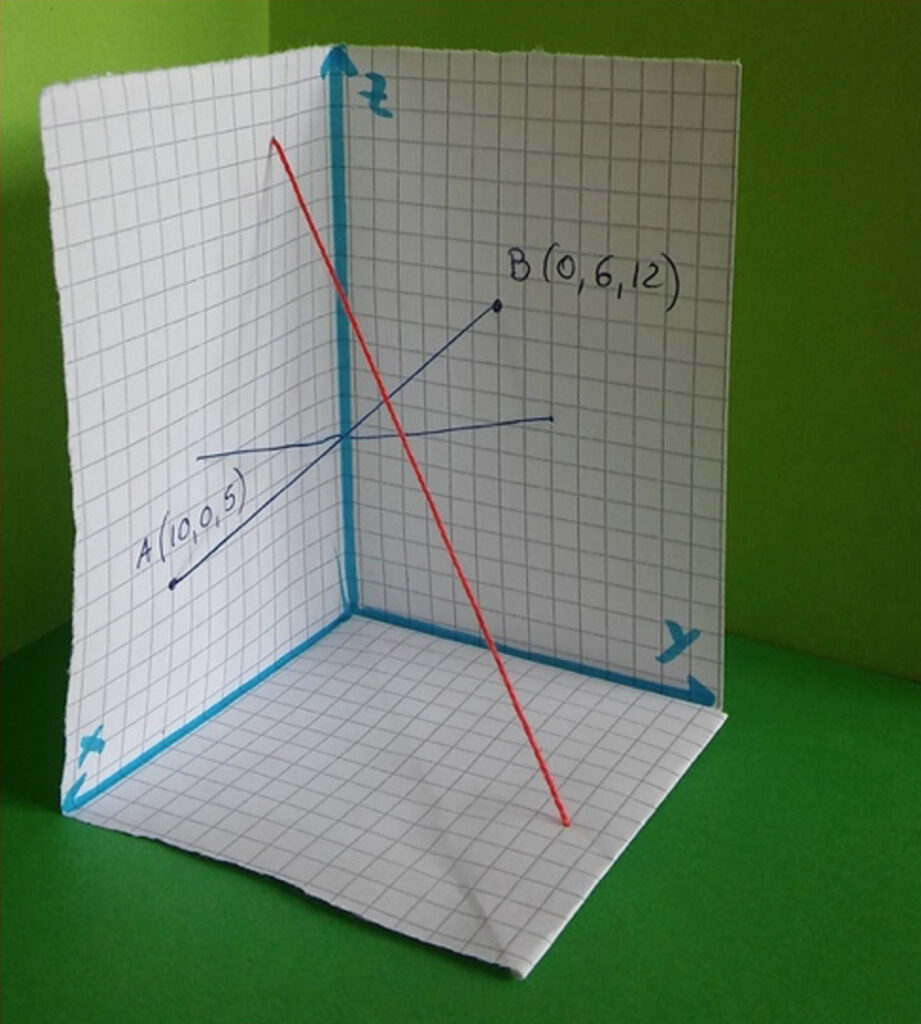
a) Che posizione reciproca possono avere due piani nello spazio? Mostrala usando il triedro, utilizzando anche altre porzioni di fogli di carta.
b) Che posizione reciproca possono avere due rette nello spazio? Sono sempre contenute in un piano?
Se non si intersecano, sono necessariamente parallele?
Puoi prendere ago e filo e “cucire” coppie di rette che hanno posizioni reciproche differenti.
Se volete usare il modello per la descrizione analitica di alcuni elementi geometrici e dello studio delle loro posizioni reciproche, potete seguire le indicazioni della scheda che trovate in Zona Matematica, nell’area dedicata agli Origami, dove propongo di “cucire”, con ago e filo, alcune rette, seguendo precise indicazioni matematiche.
