
Delle varie proprietà godute dalle quattro operazioni, la proprietà distributiva della moltiplicazione rispetto all’addizione e alla sottrazione è l’unica che coinvolga due operazioni e a volte può sembrare un po’ magica agli studenti.
Come è noto, la proprietà dice che se si deve moltiplicare un numero per una somma (o per una differenza), si può moltiplicare quel numero per ciascun addendo (o per il minuendo e per il sottraendo) e poi addizionare (o sottrarre) i prodotti parziali ottenuti.
Questa definizione può risultare faticosa per gli studenti ma possiamo renderla più tangibile con una piccola attività origami. Possiamo poi completare l’esperienza facendo piegare un semplice modello che resti agli studenti come ricordo.
Distribuite due fogli di carta rettangolare in formato A6 o A7 (ottenuti dividendo in quattro o otto parti uguali un foglio A4 da fotocopie).
Preso il primo foglio di carta, ogni studente piega un segmento parallelo a uno dei lati e lo riapre (Figura 1). Se si volesse già richiamare il modello che piegheremo alla fine si potrà indicare di piegare parallelamente al lato lungo.

Si ottiene una suddivisione della figura iniziale. La Figura 1 mostra la piega e indica le misure $a$, $b$ e $c$ da dare rispettivamente al lato lungo e a ognuno dei due segmenti in cui è diviso il lato corto.
Chiediamo ora agli studenti di proporre alcuni modi di calcolare l’area $A$ del foglio. Dopo averli lasciati interagire a coppie, scambiandosi opinioni, raccogliamo con loro le idee.
Guidiamo la discussione in modo che vengano evidenziate queste due modalità di calcolo:
- $A = a\left( {b + c} \right)$ (se leggiamo il rettangolo globalmente);
- $A = ab + ac$ (se leggiamo il rettangolo come somma dei due più piccoli nei quali è scomposto).
Poiché l’area è la stessa, si avrà: $A = a\left( {b + c} \right)=ab+ac$ e avremo così trovato la proprietà distributiva della moltiplicazione rispetto all’addizione.
Possiamo proporre una generalizzazione. Su un secondo foglio ogni studente può piegare, e riaprire, due pieghe parallele. La Figura 2 mostra le pieghe e le misure $a$, $b$, $c$ e $d$ da dare rispettivamente al lato lungo e a ognuno dei tre segmenti in cui è diviso il lato corto.

Come nel caso precedente, chiediamo di calcolare l’area del rettangolo in più modi. La discussione inviterà a fare emergere le seguenti formule per l’area:
- $A = a\left( {b + c + d} \right)$
- $A = ab + a\left( {c + d} \right)$
- $A = a\left( {b + c} \right) + ad$
- $A = ab + ac + ad$
Osservando che l’area è la stessa, vale l’uguaglianza $A = a\left( {b + c + d} \right) = ab + ac + ad$ che mostra la generalizzazione della proprietà per tre addendi. Se ne potrà discutere la validità per un numero qualsiasi di addendi.
Un’idea in più
Dall’uguaglianza 1. si può passare alle 4. grazie alle 2., usando la proprietà associativa dell’addizione e la distributiva su due addendi: $a\left( {b + c + d} \right) = a\left( {b + \left( {c + d} \right)} \right) = ab + a\left( {c + d} \right)$.
Possiamo anche piegare la proprietà distributiva della moltiplicazione rispetto alla sottrazione. Su un altro foglio facciamo eseguire le pieghe della Figura 1 e inserire le stesse notazioni, indicando con $c$ la misura del segmento più grande in cui è diviso il lato corto. Chiudiamo la piega e voltiamo il foglio. Coloriamo il rettangolo composto da un solo strato di carta, come mostra la Figura 3.
Come possiamo calcolare la sua area?

Dopo una breve discussione otteniamo $A = a\left( {c – b} \right)$ (considerando direttamente il rettangolo colorato) e $A = ac – ab$ (considerando il rettangolo come differenza del rettangolo di lati $a$, $c$ e quello di lati $a$, $b$). Si ha $A = a\left( {c – b} \right) = ac – ab$ e resta così visualizzata la proprietà.
Per chiudere in bellezza
Non si può finire una lezione origami senza piegare un modello da portare a casa che richiami l’attività svolta. Ecco il diagramma di una semplice busta (modello tradizionale) dove inserire la formula magica della proprietà distributiva (Figura 4).
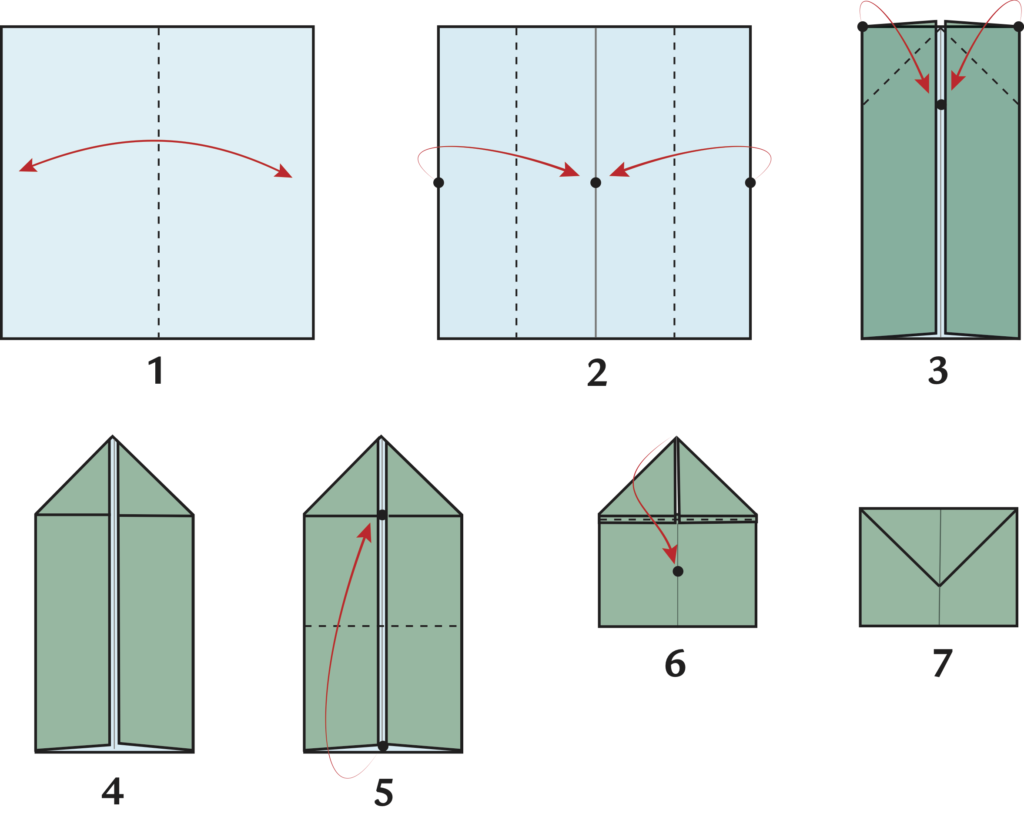
Figura 4 – Diagrammi di F. Decio, dal libro “Ed Ora, Origami”, E. Frigerio, M.L. Spreafico, Ed. Kangourou
