
Per le vacanze di Pasqua lasciamo agli studenti un’attività matematica abbinata a un modello origami tradizionale: il bicchiere, che si può usare in questa occasione come portauovo.

Questo modello si presta a riflessioni matematiche di diversa complessità; darò qualche spunto per studenti di scuola secondaria sia di primo sia di secondo grado (primo biennio).
Cominciamo col dare le indicazioni di piega, riferite al diagramma. Utilizziamo un foglio di lato circa $15$ cm, bicolore (nel diagramma, azzurro e verde). Se siete in DAD, fate ritagliare un quadrato da un foglio a quadretti: i ragazzi potranno colorare le due facce (o anche una sola), prima di iniziare a piegare.
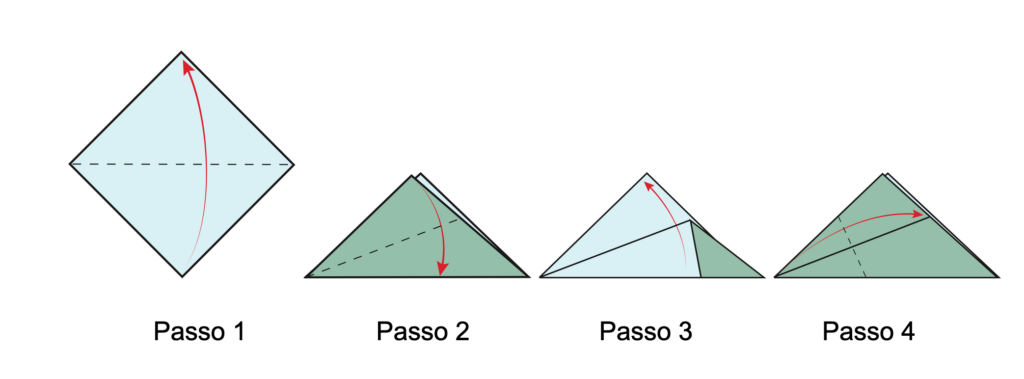
Breve spiegazione di piegatura:
1. Azzurro sopra, piegare una delle diagonali del quadrato.
2. Il triangolo ottenuto è rettangolo isoscele. Portare uno dei cateti sull’ipotenusa e piegare; si ottiene la figura bicolore del passo 3.
3. Riaprire l’ultima piega fatta.
4. La piega precedente parte da un vertice, che chiamiamo $A$, dell’ipotenusa (l’altro lo indicheremo con $B$) e tocca in un punto $D$ il cateto opposto. Portare il vertice $A$ sul punto $D$ e piegare.
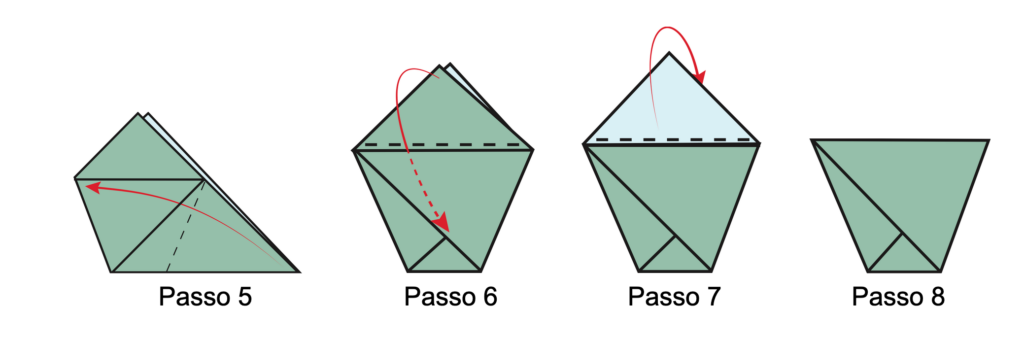
5. La figura ora è quadrangolare. Portare il vertice $B$ sul vertice a esso opposto.
6. La figura ora è un pentagono che possiamo vedere scomposto in un trapezio isoscele (da dimostrare!) sormontato da un triangolo rettangolo, in doppio strato. Piegare uno dei due strati triangolari, lungo il segmento che separa i due poligoni, intascando il triangolo nell’aletta formata in modo naturale dal triangolo isoscele (da dimostrare!) piegato nel passo 5.
7. Piegare ora a monte (cioè all’indietro) il triangolo rimasto.
8. Otteniamo così un modello che può essere aperto in corrispondenza della base maggiore del trapezio isoscele.
Ecco un’attività da proporre nella scuola secondaria di primo grado.
- Interpreta geometricamente alcune pieghe eseguite.
Per esempio: la piega da eseguire al passo 2 è la bisettrice dell’angolo di $45^{\circ }$; la piega al passo 4 è l’asse di un segmento (e questo porta poi a giustificare che il triangolo piegato è isoscele).
- Classifica i triangoli che appaiono nei vari momenti di piegatura, utilizzando i movimenti della carta come dimostrazione (quindi per verificare che due lati sono congruenti si può piegare per sovrapporli). Per esempio: quali sono tutti i triangoli rettangoli isosceli che compaiono?
Nel passo 3 appare un triangolo bicolore che ha come base l’ipotenusa del triangolo rettangolo del passo 2. Questo triangolo bicolore è diviso in due triangoli rettangoli. Si può anche chiedere di dimostrare che il triangolo verde è isoscele. Nei passi 5 e 6 appaiono altri due triangoli.
- Piega otto bicchieri (fino al passo 7). Come puoi accostarli o incastrarli per creare degli ottagoni? Sai determinare le ampiezze degli angoli dell’ottagono che hai creato? Ecco tre possibili composizioni.

Ecco un’attività da proporre nella scuola secondaria di secondo grado.
È bene riproporre il punto 1 precedente, perché può aiutare nelle dimostrazioni.
- Interpreta geometricamente alcune pieghe eseguite.
Per le due domande successive, occorre far considerare questi due passaggi con le relative notazioni sui vertici.
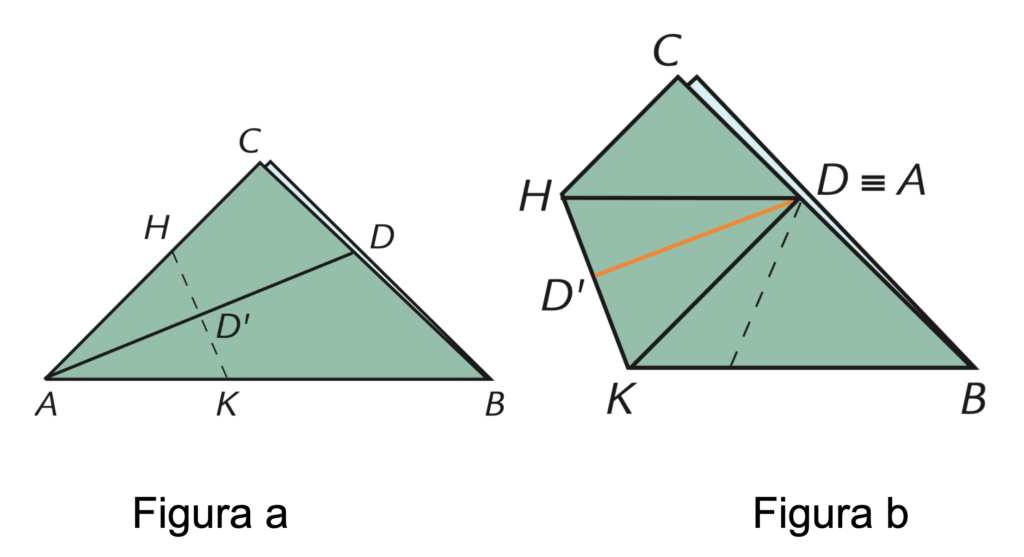
Nella figura b è meglio far disegnare ai ragazzi con una matita il segmento $DD’$ che corrisponde alla porzione di piega $AD$ (figura a) che rimane nascosta. Poiché il segmento $HK$ è l’asse di $AD$, il segmento $DD’$ è perpendicolare al segmento $HK$ e lo taglia nel suo punto medio.
- Nel passo 5, dimostra che il triangolo $HDK$ è isoscele di vertice $D$ e determina le ampiezze dei suoi angoli.
Il segmento $DD’$ è altezza del triangolo, ma anche bisettrice dell’angolo $H\widehat{D}K$, perché corrisponde a una parte del segmento $AD$. Facciamo notare che l’angolo $H\widehat{D}K$ è congruente all’angolo in $H\widehat{A}K=45^{\circ }$.
- Dimostra che il segmento $KB$ è parallelo al segmento $HD$.
Modo 1: traccia con la matita i segmenti $HD$ e $KD$ e riapri. Il quadrilatero $AHDK$ è un rombo (quattro lati congruenti); quindi $AK$ è parallelo a $HD$.
Modo 2: considera la trasversale $KD$ e guarda gli angoli alterni interni: considerando la carta piegata, $B\widehat{K}D=180^{\circ }-2H\widehat{K}D=H\widehat{D}K=45^{\circ }$; le ultime due uguaglianze sono state calcolate considerando il triangolo isoscele $HDK$.
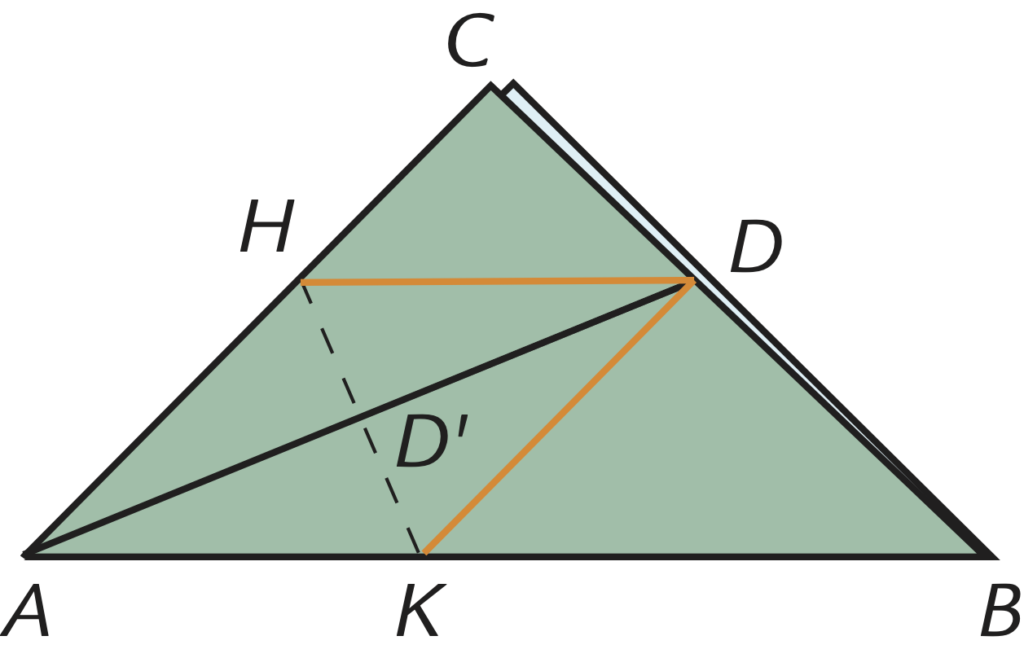
- Calcola le misure del triangolo $KBD$, indicando con $a$ la misura del lato del quadrato iniziale.
Posto $\overline{HD}=x$ abbiamo che $\overline{CD}=\dfrac{x}{\sqrt{2}}$ e $\overline{DB}=\overline{DK}=\overline{HD}=x$.
Poiché $\overline{CD}+\overline{DB}=a$ abbiamo che $\dfrac{x}{\sqrt{2}}+x=a$ da cui $x=a\sqrt{2}\left( \sqrt{2}-1\right)$.
