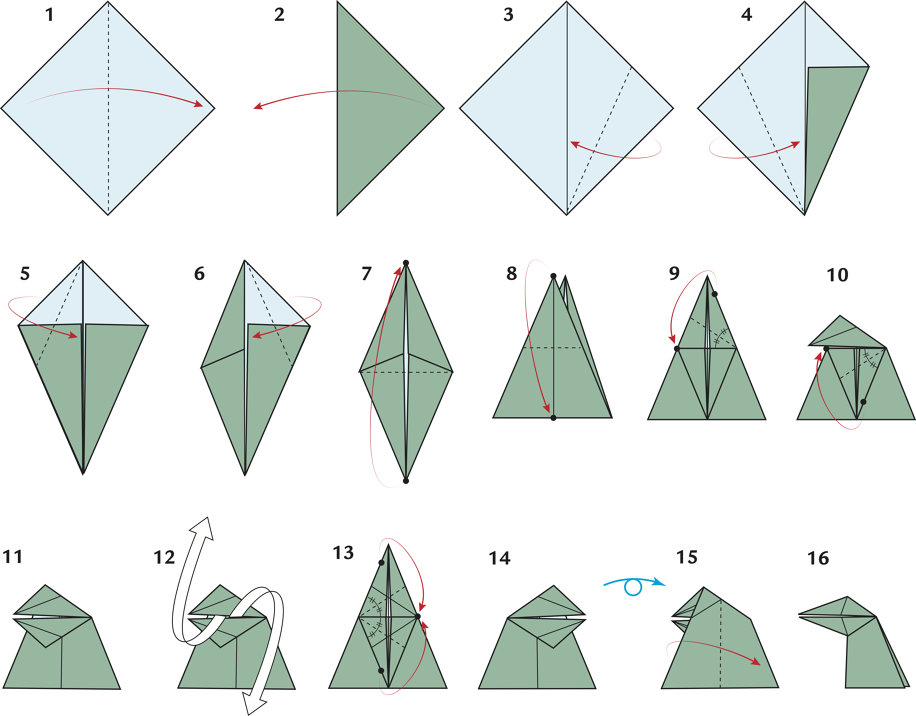
L’inscrivibilità e la circoscrivibilità dei poligoni a una circonferenza è un argomento interessante che possiamo rendere divertente e pratico con la piegatura della carta, anche in DAD.
Vi propongo di affrontarlo piegando un simpatico modello di uccellino con becco mobile: alcuni passaggi di piegatura ci offriranno l’occasione di individuare, se esistono, incentri e circocentri.
In particolare, andremo a verificare, carta alla mano, se valgono i seguenti due teoremi:
Teorema 1
Un poligono si può inscrivere in una circonferenza se e solo se gli assi dei suoi lati si incontrano in uno stesso punto (il circocentro, cioè il centro della circonferenza circoscritta).
Teorema 2
Un poligono si può circoscrivere a una circonferenza se e solo se le bisettrici dei suoi angoli interni si incontrano in uno stesso punto (l’incentro, cioè il centro della circonferenza inscritta).
Dato un poligono, il vantaggio che ci offre la carta è quello di poter piegare gli assi dei lati del poligono e le bisettrici dei suoi angoli interni.
Per ottenere l’asse di un lato $AB$, basta infatti portare $A$ su $B$: il lato si sovrapporrà a se stesso e la piega risultante ci darà l’asse.
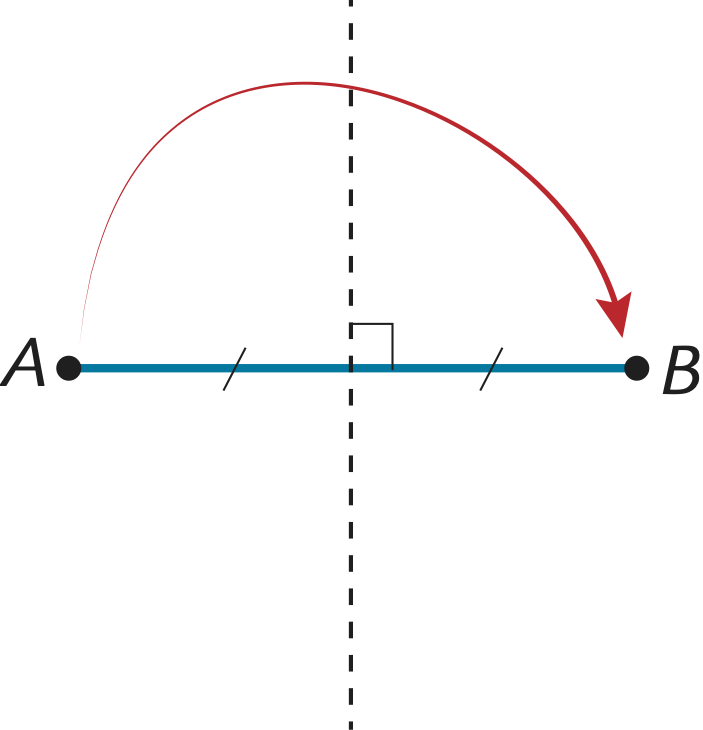
Per ottenere la bisettrice di un angolo relativo al vertice $A$, basta portare uno dei due lati uscenti da $A$ sull’altro: la piega costruita rappresenta la bisettrice dell’angolo.
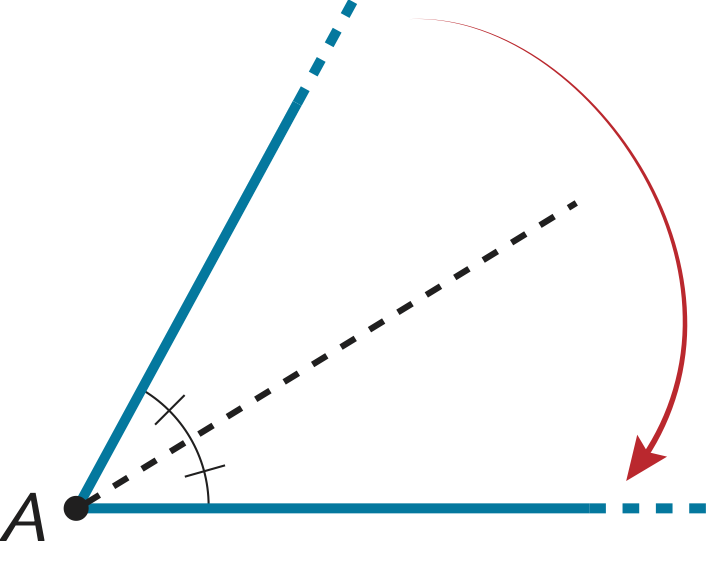
Notiamo come sia efficace la realizzazione degli assi e delle bisettrici con le pieghe: i movimenti sono molto diversi e questo permetterà agli studenti di non fare confusione sui due concetti e di astrarre poi la costruzione, individuando più facilmente questi due elementi negli esercizi di geometria.
L’idea del laboratorio sarà quella di considerare alcuni poligoni che si evidenziano naturalmente durante i vari passi di piegatura e per questi andare a verificare se gli assi dei lati e/o le bisettrici degli angoli si incontrino. Nel seguito, vi indicherò alcuni poligoni interessanti. Troverete poi in Zona Matematica i materiali di supporto all’attività (con richiami, spunti di approfondimento e tabella da compilare) che possono essere assegnati agli studenti.
Per non aggiungere troppe pieghe al modello e per poter poi tenere traccia dei poligoni analizzati, vi suggerisco di procedere così:
i. individuate i poligoni che appaiono durante la piegatura e che volete analizzare (io ne proporrò una lista durante le istruzioni di piegatura);
ii. quando, piegando, compare un poligono, fatelo ricopiare due volte su un foglio (basta appoggiarlo sul foglio e ripassarne il perimetro);
iii. fate ritagliare le due copie: gli studenti potranno piegare gli assi dei lati su una copia e le bisettrici degli angoli interni sull’altra;
iv. nei casi in cui esista la circonferenza circoscritta e/o inscritta, gli studenti potranno incollare il poligono sul quaderno e tracciare la circonferenza con il compasso. Il centro $C$ sarà dato dalle pieghe. Per quanto riguarda il raggio, nel caso della circonferenza circoscritta basterà ricordare che la circonferenza passa per i vertici del poligono. Nel caso della circonferenza inscritta si può disegnare la distanza centro-lato oppure, meglio ancora, si può trovare il punto di tangenza piegando la retta passante per $C$ e perpendicolare a un lato scelto (basta far scorrere il lato su se stesso ed eseguire la piega quando questa passa per $C$).
Siamo allora pronti a dare le istruzioni di piega!
Vi occorreranno due fogli A4 per ritagliare i poligoni e un foglio quadrato per piegare il modello. Per quanto riguarda il foglio quadrato, se non avete a disposizione carta origami, fate ritagliare un quadrato di lato $15$ cm da un foglio a quadretti.
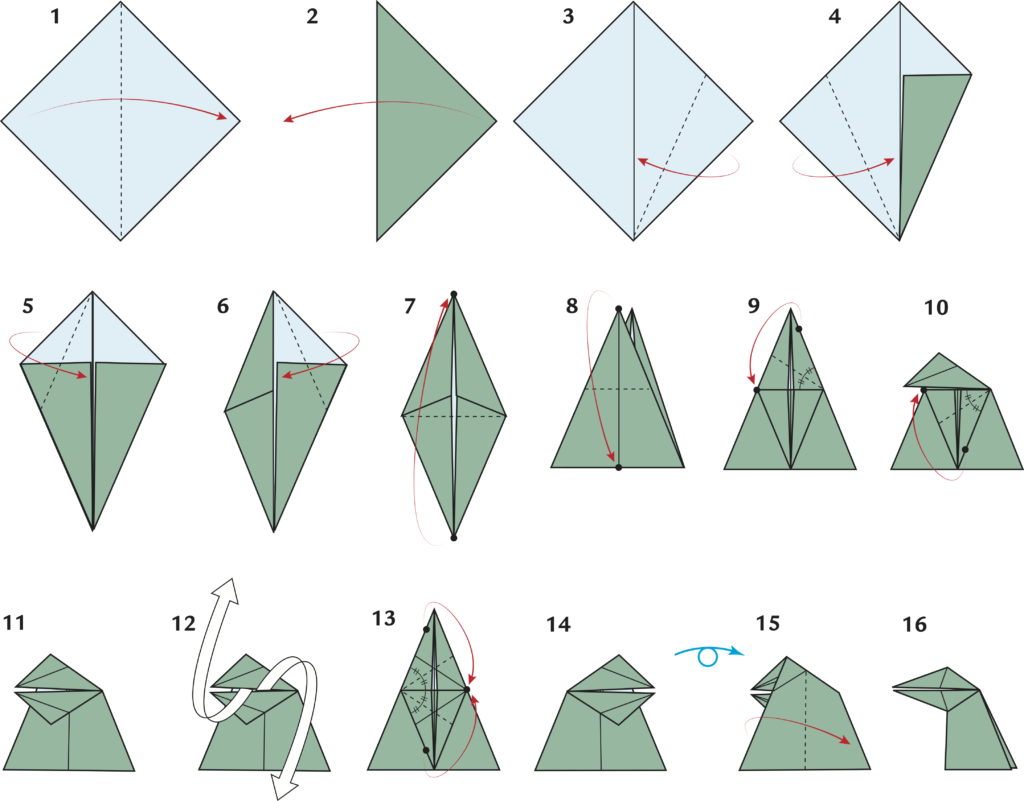
0- Azzurro sopra (nel caso si usi carta bicolore).
Il primo poligono da considerare è il quadrato di base. Come detto in precedenza, chiedete ai vostri studenti di riprodurlo (in questo caso anche in scala) per due volte su un foglio e di ritagliarlo. Chiedete di controllare con uno dei due quadrati l’intersezione degli assi dei lati e con l’altro quella delle bisettrici.
1- Piega una diagonale del quadrato. (Si ottiene un triangolo rettangolo isoscele)
2- Riapri la piega.
3- Piega un lato del quadrato sulla diagonale. (Si ottiene un quadrilatero, non regolare)
4- Porta sulla diagonale del quadrato il lato uscente dallo stesso vertice di quello considerato nel passo 3. (Si ottiene un deltoide)
5- Porta un lato corto del deltoide sull’asse di simmetria della figura. (Si ottiene un quadrilatero irregolare, come mostrato nella piega 6)
6- Piega l’altro lato corto su quella che era l’asse di simmetria del deltoide. (Si ottiene un rombo)
7- Piega lungo l’asse di simmetria più corto del rombo. (Si ottiene un triangolo isoscele)
8- Lavorando solo su uno strato di carta, porta il vertice del triangolo isoscele sul piede dell’altezza relativa alla base.
9- Nel modello si distingue un rombo interno. Porta il lato in alto a destra del rombo lungo la sua diagonale minore.
10- Sempre in riferimento al rombo precedente (ora in parte piegato), porta il lato in basso a destra lungo la diagonale minore.
11- Considera il modello che si ottiene dopo le pieghe 9 e 10.
12- Riapri le ultime due pieghe.
13- Ripeti le pieghe spiegate in 9 e 10 partendo dai lati a sinistra del rombo.
14- Considera il modello che si ottiene dopo le pieghe del punto 13. Ribalta ora il modello!
15- Piega lungo la linea perpendicolare alla base. Mentre fai questo, la parte di carta piegata in 13 tenderà a “uscire” dal modello: aiutala a prendere la forma del becco mostrato in 16.
16- Il modello è finito. È possibile far muovere il becco allontanando e avvicinando con le mani la parte posteriore del collo dell’uccellino.
Buon divertimento!
In Zona Matematica, nell’area riservata agli origami, potete trovare i materiali di supporto all’attività.
Vai all’area “Origami” del I grado
Vai all’area “Origami” del II grado – I biennio
Vai all’area “Origami” del II grado – II biennio e V anno
