
Educare a motivare le proprie affermazioni e a dimostrare le proprietà di oggetti matematici è uno degli aspetti più affascinanti ma anche più difficili della didattica della Matematica. È forse però il più importante: la Matematica è l’unica disciplina che dà la possibilità di scoprire, costruire e giustificare le proprie deduzioni: per questo può dare un contributo fondamentale per educare cittadini critici e consapevoli.
Come fare però con il tempo che manca e, soprattutto, con un programma da inseguire in questi mesi che definire complicati è un eufemismo? Credo che la risposta sia più semplice di quanto crediamo e possa essere riassunta in due considerazioni: educare al pensiero critico e alla dimostrazione è in primo luogo parte del nostro lavoro esattamente come insegnare la distinzione fra numeri razionali e irrazionali; in secondo luogo non è tempo perso, un approccio di questo tipo ai contenuti rende anzi più semplice impararli e insegnarli.
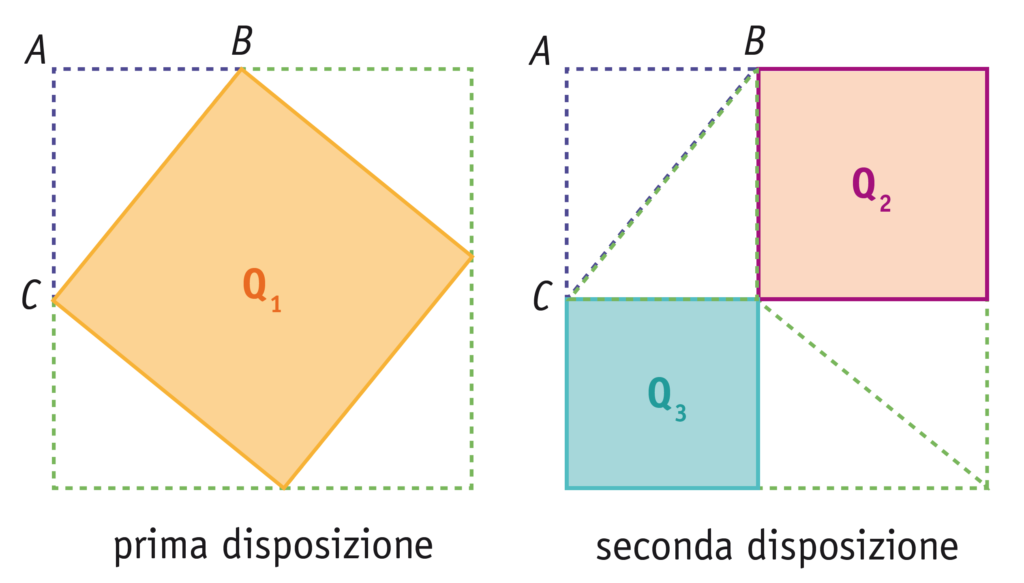
Possiamo accompagnare le nostre lezioni lungo i tre anni di scuola media con il ragionamento, la deduzione e la coscienza di poter dimostrare ciò che stiamo imparando, oppure possiamo scegliere di focalizzarci su alcuni argomenti specifici: per esempio possiamo approfondire la dimostrazione del teorema di Pitagora, utilizzando anche le numerose risorse che possiamo trovare sia nel corredo digitale del nostro libro che in rete.
In ogni caso, abbiamo molte possibilità di dedicare attività specifiche alla dimostrazione e al ragionamento. Ecco alcuni spunti:
- in prima possiamo chiedere di dimostrare se è vero che tutte (ma proprio tutte!) le potenze di 6 finiscono per 6:
$6\times 6=36$
$36\times 6=216$
$216\times 6=…$
- in seconda possiamo dimostrare che scrivere $0,\overline{9}$ e $1$ è la stessa cosa, cioè che $0,9999…$ con infiniti $9$ dopo la virgola non è affatto più piccolo di $1$:
$0,\overline{9}=\dfrac{9-0}{9}$

- in terza, con l’aiuto dei prodotti notevoli, possiamo chiedere di dimostrare che la differenza fra il quadrato di un numero naturale e il quadrato del numero precedente è sempre un numero dispari:
$\left( n+1\right) ^{2}-n^{2}=2n+1$
Le possibilità sono moltissime e aiuteremo ragazze e ragazzi a districarsi tra congetture e dimostrazioni, ipotesi e deduzioni. Se dopo aver spiegato i criteri di divisibilità giustificandone le regole capiterà invece, come è capitato a me qualche anno fa, che molto candidamente un’alunna alzi la mano per affermare che i criteri di divisibilità dipendono dal fatto che tutti i matematici del mondo si sono messi d’accordo per definirli così… vorrà dire che dobbiamo dedicare al ragionamento qualche ora in più. Ci conforta il fatto che non sarà tempo perso!
