
Rientriamo dalle vacanze invernali e proviamo ad applicare in classe terza le conoscenze acquisite su cerchio e circonferenza: seguiamo il viaggio di Babbo Natale in giro per il mondo.
Possiamo pensare alla Terra come un pianeta pressoché sferico con un raggio di circa $6400$ km. Per individuare i punti sulla superficie del nostro pianeta sono stati tracciati idealmente paralleli e meridiani.
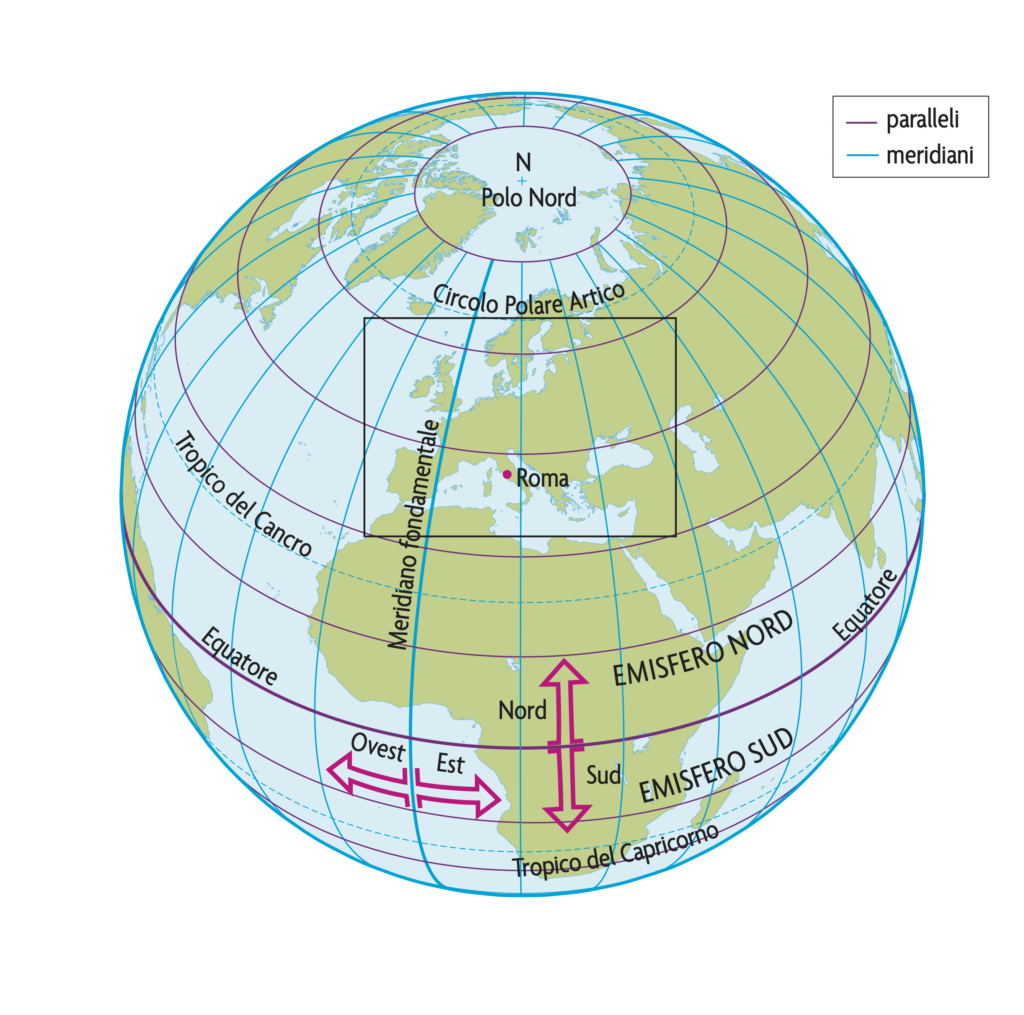
I paralleli sono linee immaginarie che corrono da ovest a est sulla superficie della Terra. Sono parallele tra loro, il che significa che sono sempre alla stessa distanza l’una dall’altra e non si incontrano mai.
Il parallelo più importante è l’Equatore, che divide la Terra in due metà dette emisferi: emisfero nord o boreale ed emisfero sud o australe. La distanza tra due paralleli si misura in gradi. L’Equatore si trova a $0^{\circ }$ di latitudine. Gli altri paralleli sono numerati a partire dall’Equatore, come per esempio il parallelo a $30^{\circ }$ nord o $60^{\circ }$ sud, e indicano la latitudine (cioè quanto ci si trova lontani dall’Equatore, spostandosi verso il Polo Nord o il Polo Sud).
I meridiani sono linee immaginarie che vanno da nord a sud, congiungono il Polo Nord al Polo Sud. Si incontrano perciò sempre ai poli. Il meridiano di riferimento è il Meridiano di Greenwich, denominato così in quanto passa per la città inglese di Greenwich e rappresenta il meridiano di longitudine $0^{\circ }$. Anche le distanze tra i meridiani si misurano in gradi. I meridiani a est o a ovest di Greenwich sono numerati da $0^{\circ }$ a $180^{\circ }$. I meridiani misurano la longitudine.
I meridiani hanno tutti la medesima lunghezza, mentre i paralleli hanno lunghezza minore quanto più sono lontani dall’equatore.
Insieme, meridiani e paralleli formano una sorta di griglia che permette di individuare qualsiasi punto sulla Terra, proprio come se fosse una grande mappa a coordinate.
Nell’immagine potete per esempio vedere la posizione di Roma e l’estensione dell’Europa.
Nella scrittura delle coordinate i punti cardinali sono indicati con le lettere delle iniziali in inglese E (est), W (ovest), N (nord), S (sud).
Il Villaggio di Babbo Natale si trova in Finlandia, più precisamente a Rovaniemi, una città situata al circolo polare artico. Le sue coordinate geografiche sono:
- Latitudine: $66.5350^{\circ }$ N
- Longitudine: $25.8550^{\circ }$ E
Babbo Natale si sposta verso Bucarest, la capitale della Romania, le cui coordinate geografiche sono:
- Latitudine: $44.4268^{\circ }$ N
- Longitudine: $25.8594^{\circ }$ E
Possiamo affermare che approssimativamente Rovaniemi e Bucarest siano situate sullo stesso meridiano. Possiamo allora chiederci: qual è l’ampiezza dell’angolo al centro che le separa? ($22.1082^{\circ }$)
Con questa affermazione possiamo determinare quanti kilometri ha percorso Babbo Natale per raggiungere la capitale della Romania, determinando la lunghezza dell’arco che unisce le due città (approssimando i gradi all’unità).
distanza $ =\dfrac{22}{360}\cdot 12.800\pi \approx 2456$ km
Babbo Natale si muove ora seguendo il parallelo di Bucarest e si ritrova nella capitale della Spagna. In questo caso è necessario approssimare di qualche grado la latitudine!). Le coordinate geografiche di Madrid sono:
- Latitudine: $40.4168^{\circ }$ N
- Longitudine: $3.7038^{\circ }$ W
Ma il raggio del parallelo a $40^{\circ }$ Nord non è di $6400$ km, bensì di $4900$ km.
Quanta strada ha percorso questa volta?
$\alpha =25.8594^{\circ }+3.7038^{\circ }=29.5632^{\circ }\approx30^{\circ }$
distanza $ =\dfrac{30}{360}\cdot 9800\pi \approx2564$ km
Come ultimo passaggio, lo seguiamo verso la capitale degli Stati Uniti. Washington, D.C. è molto vicina alla latitudine di Madrid, con una differenza di meno di $2^{\circ }$ di latitudine, e si trova anch’essa nell’emisfero settentrionale, quindi a una distanza simile dall’Equatore rispetto a Madrid. La sua longitudine è di $77.0369^{\circ }$ W. Quale distanza percorrono le renne con la slitta, in questo caso?
$\alpha =77.0369^{\circ }-3.7038^{\circ }=73.3331^{\circ }\approx73^{\circ }$
distanza $ =\dfrac{73}{360}\cdot 9800\pi \approx6240$ km
Come ultima attività si propone di analizzare queste quattro città sia sul planisfero che su Google Earth per rendersi conto di come alcune città sul nostro pianeta “sferico” siano più vicine di quanto ci possano sembrare!
Il possibile compito da assegnare può essere quello di identificare una città nell’emisfero australe che mantenga la stessa longitudine della capitale degli USA (per esempio Puerto Montt, Cile: latitudine $40.2395^{\circ }$ S, longitudine $77.0369^{\circ }$ W) e calcolare la distanza da Washington (lavorando con i meridiani, la circonferenza rimane costante e quindi è possibile utilizzare il diametro terrestre di $12.800$ km).
