
Questa attività, volta a introdurre il concetto di probabilità classica, è stata proposta in classe all’inizio di aprile, quando i sorteggi per i quarti di finale della Champions League erano stati fatti ma nessuna partita ancora giocata.
Ho riportato alla lavagna le 8 squadre partecipanti al sorteggio; questa la situazione che si presenta nelle urne (tutti gli accoppiamenti sono possibili):
Squadra |
Nazione |
| Ajax | Olanda |
| Barcellona | Spagna |
| Juventus | Italia |
| Liverpool | Inghilterra |
| Manchester City | Inghilterra |
| Manchester UTD | Inghilterra |
| Porto | Portogallo |
| Tottenham | Inghilterra |
Nel lavoro di classe abbiamo preso come riferimento l’unica squadra italiana rimasta e ci siamo domandati: “è alta la probabilità che la Juventus incontri una squadra inglese?”. Le prime risposte in classe erano contrastanti e basate su considerazioni soggettive; siamo così arrivati alla conclusione che bisognava trovare un metodo matematico che ci aiutasse. Ecco il momento di introdurre il concetto di probabilità classica con la definizione frazionaria:
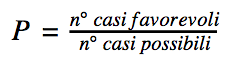
Le possibili avversarie sono 7 e le squadre inglesi sono 4, quindi la probabilità è di 4/7 che rappresenta il 57% e così abbiamo concluso che la probabilità di incontrare una squadra inglese è alta.
Le domande successive sono state formulate dagli studenti: “qual è la probabilità di incontrare una squadra iberica?”, “qual è la probabilità di incontrare una squadra del nord-Europa?”, … finché, guidati da me, abbiamo formulato la richiesta: “qual è la probabilità di incontrare una squadra francese?”. Abbiamo così potuto introdurre l’evento impossibile con P=0, provando a determinare anche un evento certo “incontrare una squadra che abbia superato gli ottavi di finale”.
Avvenuto il sorteggio, ci siamo trovati a interpretare il grafico che segue:

Per le semifinali non avverrà un nuovo sorteggio ma il cammino è già suddiviso. Allora, ci siamo posti delle nuove domande: “quale sarà la probabilità di incontrare il Porto in semifinale?” Zero. “E il Barcellona?” Ancora zero. “E il Tottenham?” Qui i ragionamenti si sono complicati e abbiamo provato a condizionare gli eventi: ipotizzando che la Juventus passi il turno, la probabilità di incontrare il Tottenham è il 50%? Sì se usiamo la probabilità classica, ma in modo semplicistico abbiamo introdotto la probabilità frequentista controllando le frequenze di vittoria/pareggio/sconfitta del Tottenham negli scontri passati. Sulle ultime 154 partite si sono avute 59 vittorie del Tottenham – 35 pareggi – 60 vittorie del Man City. Ipotizzando una sola partita (e non la doppia come in realtà) e la necessità della vittoria per il passaggio del turno la probabilità individuata è stata di 59/154 e quindi circa il 38%.
Questo lungo ragionamento ci ha portato anche a parlare di scommesse e giochi d’azzardo così da effettuare discussioni di cittadinanza attiva anche in matematica.
Leggi anche:
CRipassiamo: come ripassare matematica con l’aiuto di Cristiano Ronaldo
