
Durante le lezioni di Tecnologia, la mia classe seconda ha affrontato un progetto di educazione civica legato alla ludopatia. II percorso, finanziato dalla Regione Piemonte e facente parte del progetto regionale “Steadygap”, si intitola “IL GIOCO INFINITO – Videogiochi e azzardo tra piacere e rischio” e riguarda l’universo dei videogiochi, che possiede una rilevanza fondamentale nel panorama dei consumi mediali contemporanei, nei ragazzi come negli adulti. In particolare si evidenziano le dinamiche di consumo e alcuni possibili rischi, con un focus sulle relazioni con il gioco d’azzardo.
Abbiamo così deciso di affrontare il problema del gioco d’azzardo dal punto di vista matematico tenendo conto del fatto che in seconda media si tratta diffusamente di frazioni.
Durante la discussione di avvio dell’attività i ragazzi hanno descritto la loro esperienza con giochi on-line e in particolare con “slot-machine” in formato digitale.
Per cercare di capire meglio il funzionamento di tali software abbiamo pertanto deciso di creare una nostra slot-machine semplificata utilizzando il foglio di calcolo di Google.
A tale scopo abbiamo individuato $8$ immagini traendo spunto dalle slot con immagini di frutti.
Aperto un foglio di Google, con la funzione
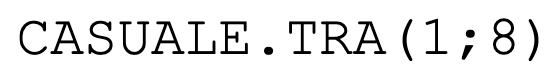
ripetuta in $9$ celle (E2:G4) abbiamo creato le $9$ caselle contenenti un numero casuale compreso tra $1$ e $8$.
Utilizzando il comando “Inserisci immagine in una cella” abbiamo inserito le $8$ immagini1 nelle celle da B1 a B8, associando a ciascuna il numero intero corrispondente nelle celle da A1 a A8 (figura a sinistra).

Per generare l’aggiornamento dei numeri casuali abbiamo scelto di inserire una “casella di controllo” (comando: “Inserisci – Casella di controllo”) nella cella I1 con dimensione del carattere $36$, sfondo rosso e tratto bianco:

Per creare l’effetto “Slot-machine” abbiamo utilizzato la funzione

utilizzandola nelle celle I2:K4.
Ecco il risultato:
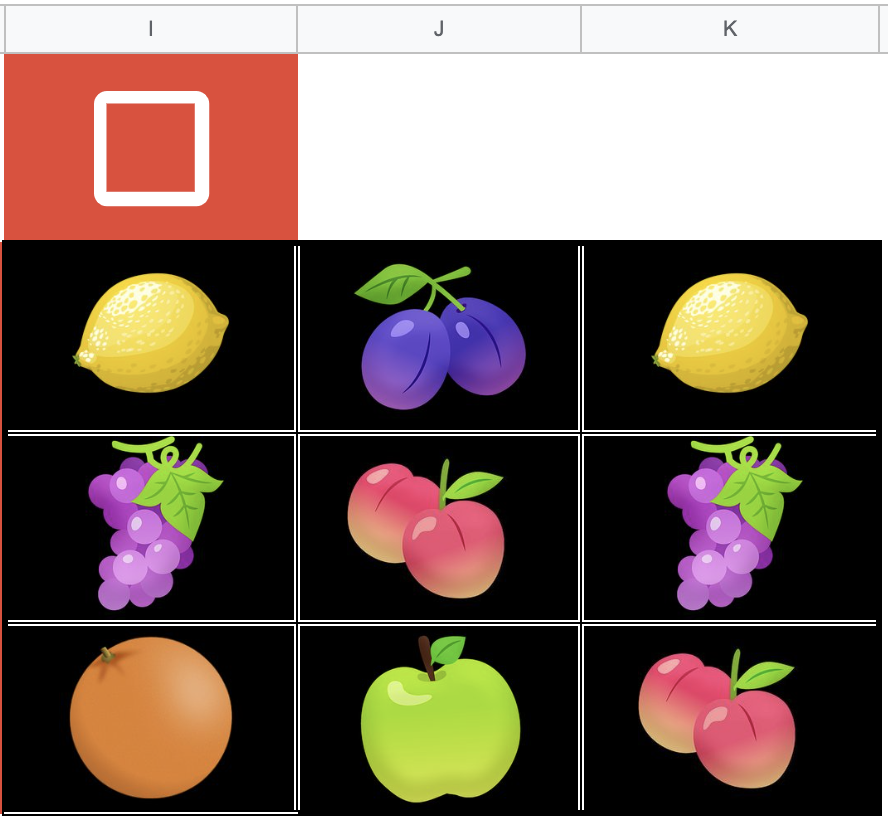
A ogni “clic” sulla casella di controllo i dati vengono aggiornati e il contenuto delle celle I2:K4 cambia generando una semplice slot machine fatta in casa.
È stato divertente per tutti provarla sul monitor interattivo in modo da poterne verificare il funzionamento. Se volete provare, a questo link potete creare una copia del file.
Abbiamo poi stabilito insieme le regole di gioco.
Per non rendere troppo complesso il funzionamento abbiamo optato per premiare solamente il caso in cui comparissero tre simboli uguali in una qualsiasi delle righe orizzontali.
Abbiamo deciso che l’insegnante sarebbe stata il “banco” e ciascun alunno avrebbe dovuto produrre $10$ gettoni di cartoncino, ciascuno di valore $1$ MUV (la nostra moneta personalizzata).
Ogni partecipante al gioco sarebbe venuto alla lavagna e avrebbe avuto due tentativi a disposizione, giocandosi $1$ gettone per volta, in caso di mancata vincita il gettone restava al “banco”.
La discussione si è fatta complessa quando si è trattato di decidere il valore della vincita da assegnare a chi otteneva la terna di immagini uguali.
Non avendo ancora inserito il discorso all’interno del calcolo delle probabilità, abbiamo deciso di assegnare al vincitore $5$ gettoni oltre a quello giocato.
Dopo $50$ tentativi il risultato era il seguente:
- $3$ vincite per un totale di $15$ gettoni pagati
- $47$ casi in cui il banco aveva incassato il gettone
Pertanto il banco, partito da $0$, disponeva ora di $32$ gettoni!
Abbiamo continuato a giocare.
Dopo $100$ tentativi il risultato era il seguente:
- $5$ vincite per un totale di $25$ gettoni pagati
- $95$ casi in cui il banco ha incassato il gettone
Pertanto il banco, ora, disponeva di $70$ gettoni!
L’osservazione dei ragazzi è stata unanime: “il banco è quello che vince quasi sempre!”
Tutti gli allievi stavano perdendo e i “soldi” per tutto questo chi li aveva messi? Tutti loro, il banco non aveva messo nulla e aveva solo incassato!
Per cercare di comprendere meglio cosa accadeva abbiamo pertanto ripreso il concetto di probabilità di un evento aleatorio (già affrontato in classe in contesti più semplici) ricordando la definizione di probabilità come frazione avente per denominatore il numero totale degli eventi possibili e numeratore il numero degli eventi favorevoli.
Ecco che allora la probabilità che in una casella comparisse il “limone” era di $\frac{1}{8}$ e così per ognuna delle altre immagini.
Se però consideravamo $2$ caselle allora i casi possibili diventavano $8\times 8=8^{2}$ e se le caselle diventavano $3$ i casi possibili erano $8\times 8\times 8=8^{3}=512$ e il caso che faceva vincere era uno solo, quindi la probabilità diventava $\frac{1}{512}$.
Considerato che era indifferente quale immagine si ripetesse, dovevamo moltiplicare per $8$ i casi favorevoli e considerato poi che le righe a disposizione erano tre, avremmo avuto il triplo degli eventi favorevoli e allora abbiamo portato la probabilità a $\dfrac{1\times 8\times 3}{512}=\frac{24}{512}=\frac{3}{64}$.
Abbiamo ottenuto così una frazione ridotta ai minimi termini che, per semplificare il ragionamento, abbiamo approssimato a $\frac{3}{63}$ per far sì che si potesse ancora semplificare in $\frac{1}{21}$. Abbiamo allora compreso che, mediamente, ci dovevamo attendere una vincita circa ogni $21$ tentativi.
Questa attività ci ha permesso di riflettere sui vari giochi che esistono nella nostra società, partendo dalle slot si è parlato di gioco del lotto, del superenalotto, dei gratta e vinci. Ci ha aiutato con i conti e le rappresentazioni spaziali un video prodotto dal Politecnico di Milano reperibile a questo link.
Un approfondimento possibile che segue questa attività è dedicato al gioco equo, ma si rende necessario introdurre il concetto di speranza matematica, che non risulta particolarmente semplice per i ragazzi di seconda.
1 Le immagini nel file sono state prese da https://pixabay.com/
