
Alcune figure geometriche sono ovunque attorno a noi. Osservando gli oggetti che ci circondano è inevitabile notare cerchi, quadrati, rettangoli e triangoli.
C’è una figura geometrica che non è così comune come altre ma che ha delle interessanti applicazioni in diversi ambiti, si tratta del triangolo di Reuleaux.
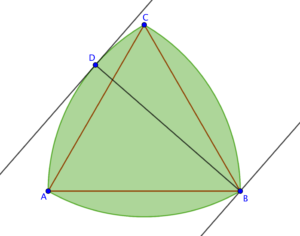
Per disegnarlo si parte da un triangolo equilatero e si tracciano i tre archi di circonferenza che hanno centro in un vertice del triangolo e che congiungono gli altri due vertici. Il triangolo di Reuleaux è l’insieme dei punti interni ai tre archi di circonferenza.
Questa particolare figura si può trovare come elemento architettonico in molte chiese gotiche per rappresentare la Trinità o come variante più slanciata e dinamica di una semplice circonferenza.

Spesso anche i plettri usati per suonare la chitarra hanno questa forma in modo da poter pizzicare le corde con una qualsiasi delle tre “punte”.
Il triangolo di Reuleaux ha una particolare proprietà: si tratta di una figura con ampiezza costante. Se cerchiamo di misurare il suo spessore usando una coppia di rette parallele ci accorgiamo che in qualsiasi modo siano inclinate le due rette, lo spessore misurato è sempre lo stesso ed è uguale al raggio con cui sono stati tracciati i tre archi di circonferenza.
Grazie al fatto di avere uno spessore costante il triangolo di Reuleaux può ruotare all’interno di un quadrato toccando in ogni posizione tutti e quattro i suoi lati.
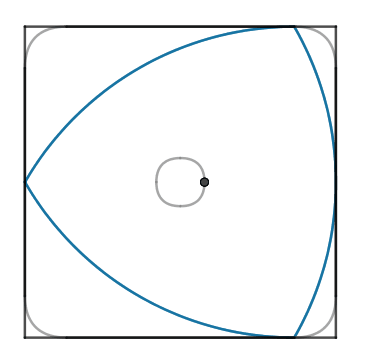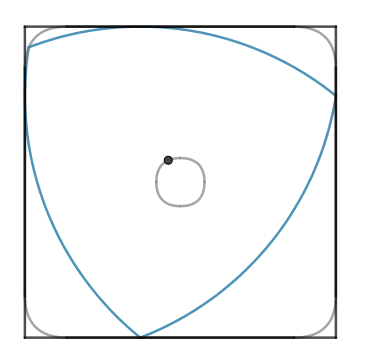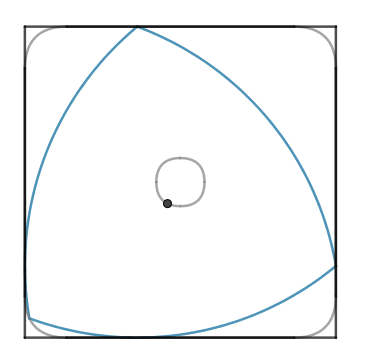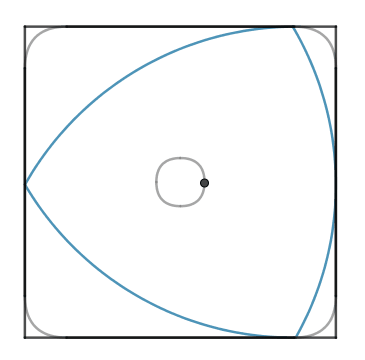
In questo movimento il centro del triangolo ruota con un verso contrario rispetto alla rotazione del triangolo (nel nostro caso il triangolo ruota in senso orario mentre il centro del triangolo ruota in senso antiorario). In questo movimento il triangolo copre gran parte dell’area del quadrato, circa il $98,77$%. Esistono dei particolari trapani con delle punte che hanno una sezione a forma di triangolo di Reuleaux e che (facendo ruotare il centro della punta su una circonferenza oltre che su se stesso) permettono dicreare dei fori quasi perfettamente quadrati!
Dopo aver spiegato ai vostri studenti come si costruisce il triangolo di Reuleaux e i suoi possibili utilizzi, come esercizio per casa potete chiedere ai vostri alunni di calcolarne il perimetro e l’area (dato il raggio) e cercare di capire qual è l’ampiezza dei suoi vertici.
