
Un modo per mostrare agli studenti l’utilità della matematica nell’affrontare questioni che si incontrano nella vita reale è risolvere insieme un problema di ottimizzazione lineare come quello che vi propongo.
Un falegname sa costruire due tipi di oggetti: tavoli e sedie. Ciascun pezzo prodotto fornirà un guadagno ma richiede una certa quantità di legna e un certo numero di ore di lavoro secondo la seguente tabella.
| Guadagno (€) | Legna necessaria (kg) | Ore di lavoro (h) | |
| Tavolo | $60$ | $5$ | $1,5$ |
| Sedia | $50$ | $2$ | $2$ |
Ogni settimana il falegname vuole lavorare non più di $44$ ore e ha a disposizione da parte del suo fornitore un massimo di $100$ kg di legna da utilizzare.
Rispettando questi vincoli quanti tavoli e sedie dovrebbe costruire il falegname per guadagnare il più possibile?
Se costruisse solamente tavoli, usando i $100$ kg di legna potrebbe fabbricare $20$ tavoli e guadagnerebbe $20 \cdot 60=1200$ euro.
Se costruisse solamente sedie, con le $44$ ore a disposizione potrebbe fabbricare $22$ sedie guadagnando $50 \cdot 22=1100$ euro. Tra i due tentativi più semplici il primo offre un maggiore guadagno.
Eppure, nessuna di queste due scelte è quella vincente.
Traduciamo il problema in una forma matematica. Indichiamo con $x$ il numero di tavoli e con $y$ il numero di sedie costruiti ogni settimana.
Le due variabili devono rispettare i vincoli:
Le variabili $x$ e $y$ devono anche soddisfare i vincoli $x \ge 0$ e $y \ge 0$. Ciascuno di questi vincoli è rappresentato da un semipiano nel piano cartesiano, per cui la regione del piano all’interno della quale si deve trovare la soluzione ottimale è un quadrilatero formato dall’intersezione di questi quattro semipiani.
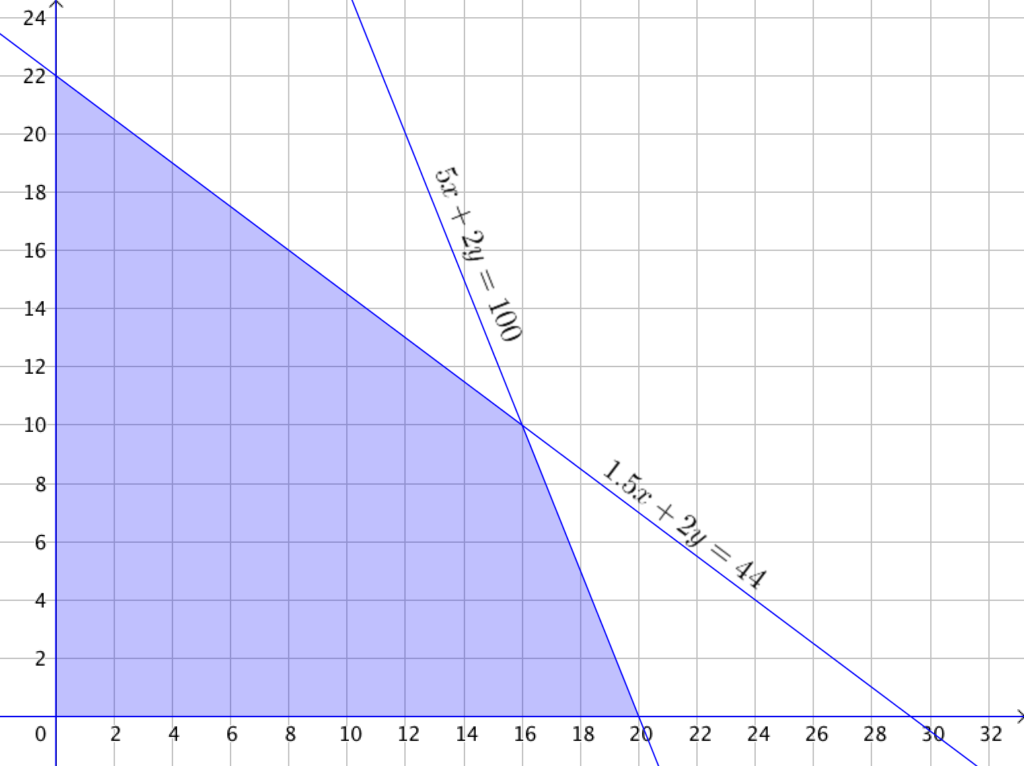
In questa regione dobbiamo trovare il punto in cui la funzione di guadagno $g\left( {x,y} \right) = 60x + 50y$ ha il valore massimo.
Immaginiamo di fissare un certo guadagno, per esempio $700$ euro. Le coppie $\left( {x,y} \right)$ che forniscono tale guadagno sono quelle che soddisfano l’equazione $60x + 50y = 700$ e si trovano quindi su una retta.
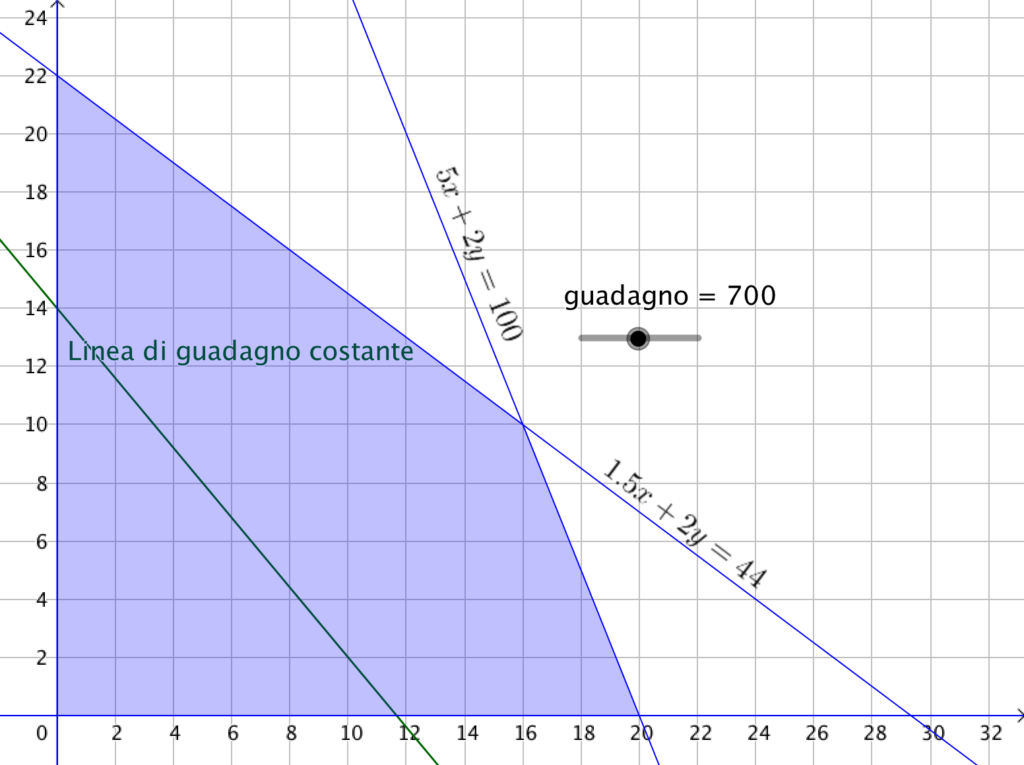
Le rette che si ottengono cambiando il parametro del guadagno formano un fascio di rette parallele. Possiamo provare ad aumentare il guadagno per trovare graficamente la soluzione, utilizzando GeoGebra.
Il miglior risultato si ottiene nel punto di intersezione delle due rette dei vincoli, per una combinazione di $16$ tavoli e $10$ sedie, con un guadagno di $1460$ euro.
Usando l’istinto probabilmente avremmo scelto di concentrarci su un prodotto o l’altro, considerando solo una delle due ipotesi semplici (e perdendo possibili guadagni). Queste due soluzioni non ottimali sono rappresentate dalle intersezioni delle rette dei vincoli con gli assi cartesiani, sono cioè i punti $\left( {20,0} \right)$ e $\left( {0,22} \right)$.
Si può ragionare con gli studenti sul fatto che se il coefficiente angolare del fascio di rette parallele fosse diverso una delle due soluzioni “semplici” potrebbe diventare quella ottimale.
Modelli analoghi si possono trovare in vari ambiti aziendali come la gestione della produzione (per esempio quanto produrre tra vari derivati del petrolio), il marketing (come distribuire una campagna di marketing su più canali), la gestione delle risorse umane (quante persone collocare in ciascun ufficio).
In tutti questi settori (e altri ancora) la matematica e il ragionamento logico sono strumenti fondamentali per poter prendere le decisioni migliori.
